8.8: How The Enthalpy Change for a Reaction Depends on Temperature
- Page ID
- 152071
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Section 8.6, we see how to use tabulated enthalpies of formation to calculate the enthalpy change for a particular chemical reaction. Such tables typically give enthalpies of formation at a number of different temperatures, so that the enthalpy change for a given reaction can also be calculated at these different temperatures; it is just a matter of repeating the same calculation at each temperature.
We often need to find the enthalpy change associated with increasing the temperature of a substance at constant pressure. As we observe in §1, this enthalpy change is readily calculated by integrating the heat capacity over the temperature change. We may want to know, for example, the enthalpy change for increasing the temperature of one mole of methane from 300 K to 400 K, with the pressure held constant at one bar. In Table 1, we find
\[ \Delta_fH^o\left(CH_4 ,g,300\, K\right) =-74.656\ \mathrm{k}\mathrm{J}\ \mathrm{mol}^{-1} \nonumber \]
\[ \Delta_fH^o\left(CH_4\mathrm{,g,400\ K}\right) = -77.703\ \mathrm{k}\mathrm{J}\ \mathrm{mol}^{-1} \nonumber \]
We might be tempted to think that the difference represents the enthalpy change associated with heating the methane. This is not so! The reason becomes immediately apparent if we consider a cycle in which we go from the elements to a compound at two different temperatures. For methane, this cycle is shown in Figure 3.

The difference between the standard enthalpies of formation of methane at 300 K and 400 K reflects the enthalpy change for increasing the temperatures of all of the reactants and products from 300 K to 400 K. That is,
\[\Delta_fH^o\left(CH_4\mathrm{,g,400\ K}\right)-\Delta_fH^o\left(CH_4\mathrm{,g,300\ K}\right) \nonumber \] \[=\int^{400}_{300}{C_P\left(CH_4\mathrm{,g}\right)dT}-\int^{400}_{300}{C_P\left(C\mathrm{,s}\right)dT} -2\int^{400}_{300}{C_P\left(H_2\mathrm{,g}\right)dT} \nonumber \]
Over the temperature range from 300 K to 400 K, the heat capacities of carbon, hydrogen, and methane are approximated by \(C_P=a+bT\), with values of \(a\) and \(b\) given in Table 1. From this information, we calculate the enthalpy change for increasing the temperature of one mole of each substance from 300 K to 400 K at 1 bar: \(\Delta H\left(C\right)=1,029\ \mathrm{J}\ {\mathrm{mol}}^{-1}\), \(\Delta H\left(H_2\right)=2,902\ \mathrm{J}\ {\mathrm{mol}}^{-1}\), and \(\Delta H\left(CH_4\right)=3,819\ \mathrm{J}\ {\mathrm{mol}}^{-1}\). Thus, from the cycle, we calculate:
\[\Delta_fH^o\left(CH_4\mathrm{,g,400\ K}\right)=-74,656+3,819-1,029-2\left(2,902\right)\ \mathrm{J}\ {\mathrm{mol}}^{-1}=\ -77,670\ \mathrm{J}\ {\mathrm{mol}}^{-1} \nonumber \]
The tabulated value is \(-77,703\ \mathrm{J}\ {\mathrm{mol}}^{-1}\). The two values differ by \(33\ \mathrm{J}\ {\mathrm{mol}}^{-1}\), or about 0.04%. This difference arises from the limitations of the two-parameter heat-capacity equations.
As another example of a thermochemical cycle, let us consider the selective oxidation of methane to methanol at 300 K and 400 K. From the enthalpies of formation in Table 1, we calculate the enthalpies for the reaction to be \(\Delta_rH^o\left(3\mathrm{00\ K}\right)=-126.412\ \mathrm{k}\mathrm{J}\ {\mathrm{mol}}^{-1}\) and \(\Delta_rH^o\left(4\mathrm{00\ K}\right)=-126.919\ \mathrm{k}\mathrm{J}\ {\mathrm{mol}}^{-1}\). As in the previous example, we use the tabulated heat-capacity parameters to calculate the enthalpy change for increasing the temperature of one mole of each of these gases from 300 K to 400 K at 1 bar. We find: \(\Delta H\left(CH_3OH\right)=4,797\ \mathrm{J}\ {\mathrm{mol}}^{-1}\), \(\Delta H\left(CH_4\right)=3,819\ \mathrm{J}\ {\mathrm{mol}}^{-1}\), and \(\Delta H\left(O_2\right)=2,975\ \mathrm{J}\ {\mathrm{mol}}^{-1}\).
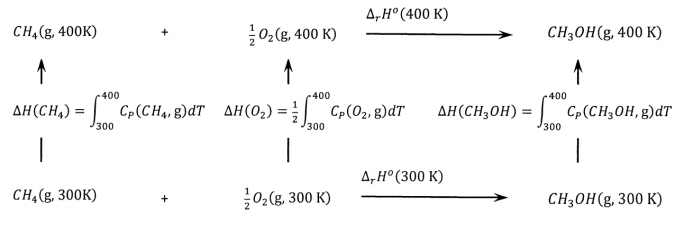
The cycle is shown in Figure 4. Inspecting this cycle, we see that we can calculate the enthalpy change for warming one mole of methanol from 300 K to 400 K by summing the enthalpy changes around the bottom, left side, and top of the cycle; that is,
\[\Delta H\left(CH_3OH\right)=126,412+3,819+\left(\frac{1}{2}\right)2,975-126,919\ \mathrm{J}\ {\mathrm{mol}}^{-1}=4,800\ \mathrm{J}\ {\mathrm{mol}}^{-1} \nonumber \]
This is 3 J or about 0.06 % larger than the value obtained \(\left(4,797\ \mathrm{J}\right)\) by integrating the heat capacity for methanol.


