8.2: Using Thermochemical Cycles to Find Enthalpy Changes
- Page ID
- 151705
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)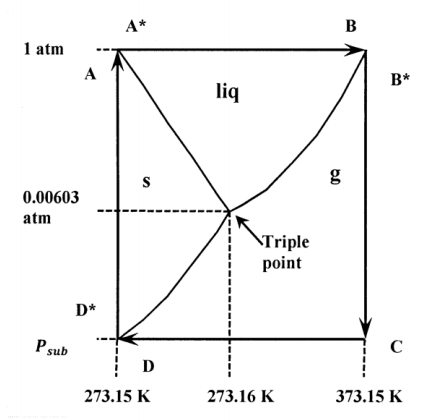
Because enthalpy is a state function, the enthalpy change in going between any two states of a system is independent of the path. For a series of changes that restore a system to its original state, the sum of all the enthalpy changes must be zero. This fact enables us to find the enthalpy changes for many processes for which it is difficult to measure heat and work directly. It is easiest to see what is involved by considering a specific example. Figure 1 shows a cyclic path, A\(\mathrm{\to }\)A*\(\mathrm{\to }\)B\(\mathrm{\to }\)…\(\mathrm{\to }\)A, superimposed on a not-to-scale presentation of the phase diagram for water. Let us look at the sublimation of ice at the melting point of pure water. The sublimation of ice is the conversion of pure ice to pure water vapor. (The melting point of pure water is the temperature at which pure ice is at equilibrium with pure liquid water at a pressure of one atmosphere; it is represented by points A and A* on the diagram. We want to find the enthalpy of sublimation at the temperature and pressure represented by points D and D*.)
Points A, A*, D, and D* are all at the same temperature; this temperature is about 273.153 K or 0.003 C. (This temperature is very slightly greater than 273.15 K or 0 C—which is the temperature at which ice and water are at equilibrium in the presence of air at a total pressure of one atmosphere.) We want to calculate the enthalpy change for the equilibrium conversion of one mole of ice to gaseous water at the pressure where the solid–gas equilibrium line intersects the line \(T=\mathrm{273.153\ K}\approx \mathrm{0\ C}\).
On the diagram, this sublimation pressure is represented as \(P_{sub}\) and the sublimation process is represented as the transition from D* to D. \(P_{sub}\) is less than the triple-point pressure of \(\mathrm{611\ Pa}\) or \(6.03\times {10}^{-3}\ \mathrm{atm}\). However, the difference is less than \(1.4\times {10}^{-5}\ \mathrm{atm}\) or \(\mathrm{1.4\ Pa}\). In equation form, the successive states traversed in this cycle are:
A (ice at 0 C and 1 atm) \(\mathrm{\to }\)
A* (water at 0 C and 1 atm) \(\mathrm{\to }\)
B (water at 100 C and 1 atm) \(\mathrm{\to }\)
B* (water vapor at 100 C and 1 atm) \(\mathrm{\to }\)
C (water vapor at 100 C and \(P_{sub}\)) \(\mathrm{\to }\)
D (water vapor at 0 C and \(P_{sub}\)) \(\mathrm{\to }\)
D*(ice at 0 C and \(P_{sub}\)) \(\mathrm{\to }\)
A (ice at 0 C and 1 atm)
We select these steps because it is experimentally straightforward to find the enthalpy change for all of them except the sublimation step (D*\(\mathrm{\to }\)D). All of these steps can be carried out reversibly. This strategy is useful in general. We make extensive use of reversible cycles to find thermodynamic information for chemical systems. The enthalpy changes for these steps are
\(H_2O\) (s, 0 C, 1 atm) \(\mathrm{\to }\) \(H_2O\) (liq, 0 C, 1 atm) \[\Delta H\left(\mathrm{A}\mathrm{\to }{\mathrm{A}}^{\mathrm{*}}\right)={\Delta }_{fus}H \nonumber \]
\(H_2O\) (liq, 0 C, 1 atm) \(\mathrm{\to }\) \(H_2O\) (liq, 100 C, 1 atm) \[\Delta H\left({\mathrm{A}}^{\mathrm{*}}\mathrm{\to }\mathrm{B}\right)=\int^{372.15\ \mathrm{K}}_{273.15\ \mathrm{K}}{C_P\left(H_2O,\ \mathrm{liq}\right)\ dT} \nonumber \]
\(H_2O\) (liq, 100 C, 1 atm) \(\mathrm{\to }\) \(H_2O\) (g, 100 C, 1 atm) \[\Delta H\left(\mathrm{B}\mathrm{\to }{\mathrm{B}}^{\mathrm{*}}\right)={\Delta }_{vap}H \nonumber \]
\(H_2O\) (g, 100 C, 1 atm) \(\mathrm{\to }\) \(H_2O\) (g, 100 C, \(P_{sub}\)) \[\Delta H\left({\mathrm{B}}^{\mathrm{*}}\mathrm{\to }\mathrm{C}\right)=\int^{P=P_{sub}}_{P=1}{{\left(\frac{\partial H\left(H_2O,\ \mathrm{g}\right)}{\partial P}\right)}_T\ dP\approx 0} \nonumber \]
\(H_2O\) (g, 100 C, \(P_{sub}\)) \(\mathrm{\to }\)\(H_2O\) (g, 0 C, \(P_{sub}\)) \[\Delta H\left(\mathrm{C}\mathrm{\to }\mathrm{D}\right)=\int^{272.15\ \mathrm{K}}_{373.15\ \mathrm{K}}{C_P\left(H_2O,\ \mathrm{g}\right)\ dT} \nonumber \]
\(H_2O\) (g, 0 C, \(P_{sub}\)) \(\mathrm{\to }\) \(H_2O\) (s, 0 C, \(P_{sub}\)) \[\Delta H\left(\mathrm{D}\mathrm{\to }{\mathrm{D}}^{\mathrm{*}}\right)={-\Delta }_{sub}H \nonumber \]
\(H_2O\) (s, 0 C, \(P_{sub}\)) \(\mathrm{\to }\)\(H_2O\) (s, 0 C, 1 atm)
\[\Delta H\left({\mathrm{D}}^{\mathrm{*}}\mathrm{\to }\mathrm{A}\right)=\int^{P=1}_{P=P_{sub}}{{\left(\frac{\partial H\left(H_2O,\ \mathrm{s}\right)}{\partial P}\right)}_T\ dP\approx 0} \nonumber \] Summing the enthalpy changes around the cycle gives
\[0={\Delta }_{fus}H+\int^{372.15\ \mathrm{K}}_{273.15\ \mathrm{K}}{C_P\left(H_2O,\ \mathrm{liq}\right)\ dT}+{\Delta }_{vap}H \nonumber \] \[+\Delta H\left({\mathrm{B}}^{\mathrm{*}}\mathrm{\to }\mathrm{C}\right)+\int^{272.15\ \mathrm{K}}_{373.15\ \mathrm{K}}{C_P\left(H_2O,\ \mathrm{g}\right)\ dT}{-\Delta }_{sub}H \nonumber \] \[+\Delta H\left({\mathrm{D}}^{\mathrm{*}}\mathrm{\to }\mathrm{A}\right) \nonumber \]
Using results that we find in the next section, \(H\left({\mathrm{B}}^{\mathrm{*}}\mathrm{\to }\mathrm{C}\right)\approx 0\) and \(\Delta H\left({\mathrm{D}}^{\mathrm{*}}\mathrm{\to }\mathrm{A}\right)\approx 0\), we have
\[0={\Delta }_{fus}H+\int^{372.15\ \mathrm{K}}_{273.15\ \mathrm{K}}{C_P\left(H_2O,\ \mathrm{liq}\right)\ dT}+{\Delta }_{vap}H \nonumber \] \[\ \ +\int^{272.15\ \mathrm{K}}_{373.15\ \mathrm{K}}{C_P\left(H_2O,\ \mathrm{g}\right)\ dT}{-\Delta }_{sub}H \nonumber \]
The enthalpy of fusion, the enthalpy of vaporization, and the heat capacities are measurable in straightforward experiments. Their values are given in standard compilations, so we are now able to evaluate \({\Delta }_{sub}H\), a quantity that is not susceptible to direct measurement, from other thermodynamic quantities that are. (See Problem 8.)


