5.13: The Michaelis-Menten Mechanism for Enzyme-catalyzed Reactions
- Page ID
- 152014
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An enzyme is a molecule produced by a living organism. Its enzymes are essential to the life processes of the organism. Often enzymes are large molecules that are catalytically active only when folded into a particular conformation. Molecules whose reactions are catalyzed by an enzyme are customarily referred to as substrates for that enzyme. Two aspects of enzymatic catalysis are remarkable. First, it is often found that an enzyme can discriminate between two very similar substrates, greatly enhancing the reaction rate of one while having a much smaller effect on the rate of the other. Second, the rate enhancements achieved by enzyme catalysis are often very large; rate increases by a factor of \({\mathrm{10}}^{\mathrm{6}}\) are observed.
Simple mechanistic and kinetic models are sufficient to explain these essential features of enzyme catalysis. We consider the simplest case. Both the mechanisms and the rate laws for enzymatic reactions can become much more complex than the model we develop. (The literature of enzyme catalysis uses a specialized vocabulary. Problem 32 introduces some of this terminology and some of the mechanistic complications that can be observed.)
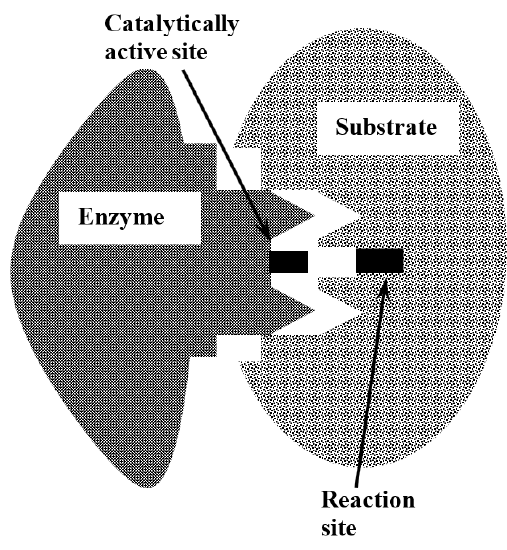
The catalytic specificity of enzymes is explained by the idea that the enzyme and the substrate have complex three-dimensional structures. These structures complement one another in the sense that enzyme and substrate can fit together tightly, bringing the catalytically active parts of the enzyme’s structure into close proximity with those substrate chemical bonds that are changed in the reaction. This is often called the lock and key model for enzyme specificity, invoking the idea that the detailed features of the enzyme’s structure are shaped to fit into the structure of its substrate, just as a key is machined to match the arrangement of tumblers in the lock that it opens. Figure 2 illustrates this idea.
The rates of enzyme-catalyzed reactions can exhibit complex dependence on the relative concentrations of enzyme and substrate. Most of these features are explained by the Michaelis-Menten mechanism, which postulates a rapid equilibration of enzyme and substrate with their enzyme-substrate complex. Transformation of the substrate occurs within this complex. The reaction products do not complex strongly with the enzyme. After the substrate has been transformed, the products diffuse away. The enzyme can then complex with another substrate molecule and catalyze its reaction. Representing the enzyme, substrate, enzyme–substrate complex, and products as \(E\), \(S\), \(ES\), and \(P\), respectively, the simplest-case Michaelis-Menten mechanism is
- Complexation equilibrium: \[ES\ \begin{array}{c} K \\ \rightleftharpoons \\ k \end{array} \ E+S \nonumber \]
- Substrate transformation: \[ES\to E+P \nonumber \]
where \(K\) is the equilibrium constant for the dissociation of the enzyme–substrate complex, and \(k\) is the rate constant for the rate-determining transformation of the enzyme–substrate complex into products.
Since the first-order decay of the enzyme–substrate complex is the product-forming step, the reaction rate is expected to be
\[\frac{d\left[P\right]}{dt}=k\left[ES\right] \nonumber \]
Letting the product concentration be \(\left[P\right]=x\) and the initial concentrations of enzyme and substrate be \(E_0\) and \(S_0\), respectively, material balance requires
\(E_0=\left[E\right]+\left[ES\right]\) and \(S_0=\left[S\right]+\left[ES\right]+x\)
Most experiments are done with the substrate present at a much greater concentration than the enzyme, \(S_0\gg E_0\). In this case, \(\left[ES\right]\) is negligible in the \(S_0\) equation, and the concentration of free substrate becomes \(\left[S\right]=S_0-x\). The enzyme-substrate equilibrium imposes the relationship
\[K=\frac{\left[E\right]\left[S\right]}{\left[ES\right]}=\frac{\left[E\right]\left(S_0-x\right)}{\left[ES\right]} \nonumber \]
Using this relationship to eliminate \(\left[E\right]\) from the expression for \(E_0\) gives
\[E_0=\frac{K\left[ES\right]}{S_0-x}+\left[ES\right]=\left(\frac{K}{S_0-x}+1\right)\left[ES\right] \nonumber \]
The rate law for product formation becomes
\[\frac{dx}{dt}=k\left[ES\right]=\frac{kE_0\left(S_0-x\right)}{K+\left(S_0-x\right)} \nonumber \]
If \(K\ll S_0-x\), the dependence on substrate cancels, and the rate law becomes pseudo-zero-order
\[\frac{dx}{dt}=kE_0=k_{obs} \nonumber \]
where the observed zero-order rate constant depends on \(E_0\). If \(K\gg S_0-x\), the rate law becomes pseudo-first-order
\[\frac{dx}{dt}=\frac{kE_0}{K}\left(S_0-x\right)=k_{obs}\left(S_0-x\right) \nonumber \]
with pseudo-first-order rate constant \(k_{obs}={kE_0}/{K}\). If neither of these simplifications is applicable, fitting experimental data to the integrated rate law becomes inconvenient.
In practice, the integrated form of the rate law is seldom used. As noted earlier, enzyme catalysis is usually studied using the method of initial rates. That is, the rate is approximated as \({dx}/{dt}\approx {\Delta x}/{\Delta t}\) by measuring the amount of product formed over a short time interval, \(\Delta t\), in which \(x\ll S_0\). The rate and equilibrium constants can then be found by fitting the rate measured at various initial concentrations, \(E_0\) and \(S_0\), to the equation
\[\frac{\Delta x}{\Delta t}\approx \frac{kE_0S_0}{K+S_0} \nonumber \]
Since the concentration of the enzyme–substrate complex is normally small compared to the concentration of the substrate, the Michaelis-Menten mechanism can also be analyzed by applying the steady-state approximation to \(\left[ES\right]\). If the product-forming step occurs so rapidly that the concentration of the enzyme–substrate complex is not maintained at the equilibrium value, the steady-state treatment becomes necessary.


