5.11: Rate Laws from Experiments in a Continuous Stirred Tank Reactor
- Page ID
- 152012
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A continuous stirred tank reactor (CSTR)—or capacity-flow reactor—is a superior method of collecting kinetic data when the rate law is complex. Unfortunately, a CSTR tends to be expensive to construct and complex to operate. Figure \(\PageIndex{1}\) gives a schematic representation of the essential features of a CSTR. Fresh reagents are fed to a reactor vessel of volume \(V\) at a constant rate. A portion of the reactor contents is continuously removed at the same volumetric flow rate. Because the addition and removal of material occur at the same rate, the reactor is always filled with a fixed volume of reaction mixture. The reaction vessel and its contents are maintained at a constant temperature. The vessel contains a stirrer, which operates continuously and at a high enough speed to keep the contents of the vessel homogeneous (free of concentration and temperature gradients) at all times.
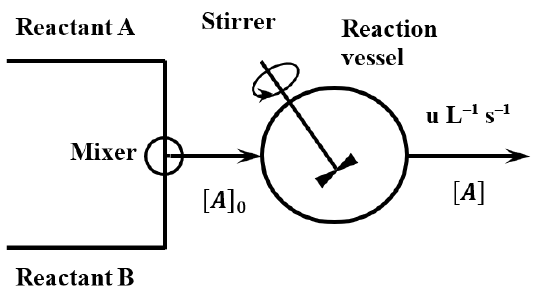
The essential idea involved in the operation of a CSTR is that, after the passage of sufficient time, the concentrations of the various species present in the reactor become constant. We say that the reactor contains steady-state concentrations of the reactants and products. When the reactor reaches this steady state, processes that increase reagent concentrations are occurring at the same rate as processes that decrease them.
Let the reaction be of the form:
\[A+B \to \mathrm{Products}. \nonumber \]
The concentrations of the reagents in the feed solution are known. Let the concentration of \(A\) in the fresh feed solution be \({\left[A\right]}_0\). Let the rate at which fresh reagent-containing solution is fed to the reactor be \(u\ {\mathrm{L}}^{\mathrm{-1}}{\mathrm{s}}^{\mathrm{-1}}\). Homogeneous reaction mixture is withdrawn from the vessel at the same flow rate. The amount of \(A\) in the reactor is increased by the flow of fresh reactant solution into the reactor. It is decreased both by reaction and by the flow of solution out of the reactor. The steady-state reaction rate, \(R=R\left(A\right)\), is the number of moles of reactant \(A\) consumed by the reaction per unit time per unit volume of reaction vessel after all of the reagent concentrations have become constant. Since \(A\) is a reactant, this rate is
\[R=-\frac{1}{V}\frac{d_rn_A}{dt} \nonumber \]
where \({d_rn_A}/{dt}\) is the contribution that the reaction makes to the rate at which the number of moles of \(A\) in the reactor changes. Since all of the reaction occurs within the vessel, and the vessel is entirely filled with the solution, \(R\) is also the number of moles of \(A\) consumed by reaction per unit time per unit volume of solution.
At steady state, the number of moles of \(A\) in the reactor is determined by:
- the number of moles of \(A\) entering the reactor per unit time,
- the number of moles of \(A\) being consumed by reaction per unit time, and
- the number of moles of \(A\) leaving the reactor in the effluent stream per unit time.
In unit time, the number of moles entering with the feed is given by \(u{\left[A\right]}_0\); the number leaving with the effluent is given by \(u\left[A\right]\). In unit time, the contribution that the reaction makes to the change in the number of moles of \(A\) present is \(-RV\). When the steady state is reached, the number of moles entering, plus the change due to reaction, must equal the number of moles leaving:
\[\textbf{moles flowing in } \mathbf{+} \textbf{ change in moles due to reaction } - \textbf{ moles flowing out } \mathbf{= 0} \nonumber \]
or, in unit time,
\[u{\left[A\right]}_0-RV-u\left[A\right]=0 \nonumber \]
Solving for \(R\), we have
\[R=-\frac{u}{V}\left(\left[A\right]-{\left[A\right]}_0\right) \nonumber \]
(We define reaction rate so that \(R>0\). If \(A\) is produced by the reaction, the mass-balance equation is \(u{\left[A\right]}_0+RV-u\left[A\right]=0\).)
As with the method of initial rates, the rate law is determined by measuring reaction rates in a series of experiments in which the steady-state concentrations of the various reactants and products vary. For each experiment it is necessary to determine both the reaction rate and the steady-state concentration of each reagent that might be involved in the rate law. Using the equation above, the rate is calculated from the difference between a reagent concentration in the feed solution and its steady-state concentration in the reactor. The concentration of each reagent in the effluent is the same as its concentration in the reactor, so the necessary concentration information can be obtained by chemical analysis of the effluent solution. The chemical analysis must be done in such a way that no significant reaction occurs between the time the material leaves the reaction vessel and the time the analysis is completed.


