4.6: Boyle's Law from the Maxwell-Boltzmann Probability Density
- Page ID
- 151681
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Chapter 2, we derive Boyle’s lawBoyle’s law using simplifying assumptions. We are now able to do this derivation much more rigorously. We consider the collisions of gas molecules with a small portion of the wall of their container. We suppose that the wall is smooth, so that we can select a small and compact segment of it that is arbitrarily close to being planar. We denote both the segment of the wall and its area as \(A\). \(A\) can have any shape so long as it is a smooth, flat surface enclosed by a smooth curve.
Let the volume of the container be \(V\) and the number of gas molecules in the container be \(N\). We imagine that we follow the trajectory of one particular molecule as it moves to hit the wall somewhere within \(A\). We begin our observations at time \(t=0\) and suppose that the collision occurs at time \(t\).
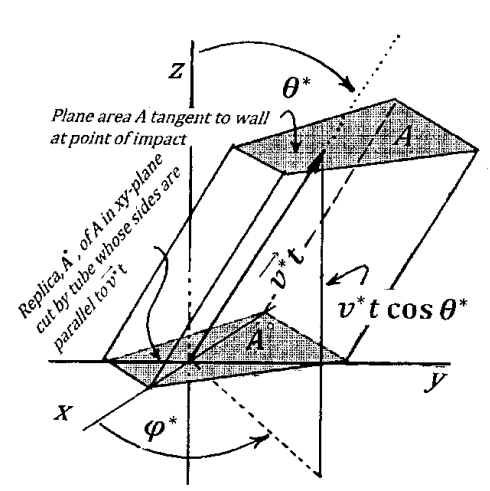
As sketched in Figure 3, we erect a Cartesian coordinate system with its origin at the location in space of the molecule at time \(t=0\). We orient the axes of this coordinate system so that the \(xy\)-plane is parallel to the plane of \(A\), and the z-axis is pointed toward the wall. Then the unit vector along the \(z\)-axis and a vector perpendicular to \(A\) are parallel to one another. It is convenient to express the velocity of the selected molecule in spherical coordinates. We suppose that, referred to the Cartesian coordinate system we have erected, the velocity vector of the selected molecule is \(\left(v^*,{\theta }^*,{\varphi }^*\right)\). The vector \(\mathop{v^*}\limits^{\rightharpoonup}t\), drawn from the origin of our Cartesian system to the point of impact on the wall, follows the trajectory of the molecule from time zero to time \(t\). The \(z\)-component of the molecular velocity vector is normal to the plane of \(A\) at the point of impact; the magnitude of the\(\ z\)-component \(v^*{\mathrm{cos} {\theta }^*\ }\). The perpendicular distance from the plane of A to the \(xy\)-plane of the Cartesian system is \(v^*t{\mathrm{cos} {\theta }^*\ }\).
We assume that the collision is perfectly elastic. Before collision, the velocity component perpendicular to the wall is \(v_z=v^*{\mathrm{cos} {\theta }^*\ }\). Afterward, it is \(v_z={-v}^*{\mathrm{cos} {\theta }^*\ }\). Only this change in the \(v_z\) component contributes to the force on the wall within \(A\). (The \(v_x\) and \(v_y\) components are not changed by the collision.) During the collision, the molecule’s momentum change is \({-2mv}^*{\mathrm{cos} {\theta }^*\ }\). During our period of observation, the average force on the molecule is thus \({\left({-2mv}^*{\mathrm{cos} {\theta }^*\ }\right)}/{t}\). The force that the molecule exerts on the wall is \({\left({2mv}^*{\mathrm{cos} {\theta }^*\ }\right)}/{t}\), and hence the contribution that this particular collision—by one molecule traveling at velocity \(v^*\)— makes to the pressure on the wall is
\[P_1\left(v^*\right)=\frac{2mv^* \mathrm{cos} {\theta }^*\ }{At} \nonumber \]
We want to find the pressure on segment \(A\) of the wall that results from all possible impacts. To do so, we recognize that any other molecule whose velocity components are \(v^*\), \({\theta }^*\), and \({\varphi }^*\), and whose location at time \(t=0\) enables it to reach \(A\) within time \(t\), makes the same contribution to the pressure as the selected molecule does. Let us begin by assuming that the velocities of all N of the molecules in the volume, \(V\), are the same as that of the selected molecule. In this case, we can find the number of the molecules in the container that can reach \(A\) within time \(t\) by considering a tubular segment of the interior of the container. The long axis of this tube is parallel to the velocity vector of the selected molecule. The sides of this tube cut the container wall along the perimeter of \(A\). This tube also cuts the \(xy\)-plane (the \(z=0\) plane) of our coordinate system in such a way as to make an exact replica of \(A\) in this plane. Call this replica \(A^o\).
The area of \(A^o\) is \(A\); the plane of \(A^o\) is parallel to the plane of \(A\); and the perpendicular distance between the plane of \(A\) and the plane of \(A^o\) is \(v^*t{\mathrm{cos} {\theta }^*\ }\). The volume of this tube is therefore \({Av}^*t{\mathrm{cos} {\theta }^*\ }\). Since there are \({N}/{V}\) molecules per unit volume, the total number of molecules in the tube is \({\left(ANv^*t{\mathrm{cos} {\theta }^*\ }\right)}/{V}\). When we assume that every molecule has velocity components \(v^*\), \({\theta }^*\), and \({\varphi }^*\), all of the molecules in the tube reach \(A\) within time \(t\), because each of them travels parallel to the selected molecule, and each of them is initially at least as close to \(A\) as is the selected molecule. Therefore, each molecule in the tube contributes \(P_1\left(v^*\right)={2mv^*{\mathrm{cos} {\theta }^*\ }}/{At}\) to the pressure at \(A\). The total pressure is the pressure per molecule multiplied by the number of molecules:
\[\left(\frac{2mv^* \mathrm{cos} {\theta }^*\ }{At}\right)\left(\frac{ANv^*t \mathrm{cos} {\theta }^*\ }{V}\right)=\frac{2mN \left(v^* \mathrm{cos} {\theta }^*\right)^2}{V} \nonumber \]
However, the molecular velocities are not all the same, and the pressure contribution \({2mN{\left(v^*{\mathrm{cos} {\theta }^*\ }\right)}^2}/{V}\) is made only by that fraction of the molecules whose velocity components lie in the intervals \({\theta }^*<\theta <{\theta }^*+d\theta\) and \({\varphi }^*<\varphi <{\varphi }^*+d\varphi\). This fraction is
\[\rho \left(v^*,{\theta }^*,{\varphi }^*\right) \left(v^*\right)^2 \mathrm{sin} {\theta }^*dvd\theta d\varphi = \left(\frac{\lambda }{2\pi }\right)^{3/2} \left(v^*\right)^2\mathrm{exp}\left(\frac{-\lambda \left(v^*\right)^2}{2}\right)\mathrm{sin} {\theta }^*dvd\theta d\varphi \nonumber \]
so that the pressure contribution from molecules whose velocity components lie in these ranges is
\[dP=\frac{2mN\left(v^* \mathrm{cos} {\theta }^* \right)^2}{V}\times \left(\frac{\lambda }{2\pi }\right)^{3/2} \left(v^*\right)^2\mathrm{exp}\left(\frac{-\lambda \left(v^*\right)^2}{2}\right) \mathrm{sin} {\theta }^*dvd\theta d\varphi \nonumber \]
The total pressure at \(A\) is just the sum of the contributions from molecules with all possible combinations of velocities \(v^*\), \({\theta }^*\), and \({\varphi }^*\). To find this sum, we integrate over all possible velocity vectors. The allowed values of \(v\) are \(0\le v<\infty\). There are no constraints on the values of \(\varphi\); we have \(0\le \varphi <2\pi\). However, since all of the impacting molecules must have a velocity component in the positive z-direction, the possible values of \(\theta\) lie in the interval \(0\le \theta <{\pi }/{2}\). We designate the velocity of the original molecule as \(\left(v^*,{\theta }^*,{\varphi }^*\right)\) and retain this notation to be as specific as possible in describing the tube bounded by \(A\) and \(A^o\). However, the velocity components of an arbitrary molecule can have any of the allowed values. To integrate (See Appendix D) over the allowed values, we drop the superscripts. The pressurepressure:on wall at \(A\) becomes
\[P=\frac{2mN}{V} \left(\frac{\lambda }{2\pi }\right)^{3/2}\times \nonumber \]
\[\int^{\infty }_0 v^4exp\left(\frac{-\lambda v^2}{2}\right)dv \int^{\pi /2}_0 \mathrm{cos}^2 \theta \ \mathrm{sin} \theta \ d\theta \int^{2\pi }_0 d\varphi \nonumber \]
\[=\frac{2mN}{V} \left(\frac{\lambda }{2\pi }\right)^{3/2}\left[ \frac{3}{8} \left(\frac{2}{\lambda }\right)^2 \left(\frac{2\pi }{\lambda }\right)^{1/2}\right]\left[\frac{1}{3}\right]\left[2\pi \right]=mN/V\lambda \nonumber \]
and the pressure–volume product becomes
\[PV=\frac{mN}{\lambda } \nonumber \]
Since \(m,\) \(N\), and \(\lambda\) are constants, this is Boyle’s law. Equating this pressure–volume product to that given by the ideal gas equation, we have \({mN}/{\lambda }=NkT\) so that
\[\lambda =\frac{m}{kT} \nonumber \]
Finally, the Maxwell-Boltzmann equation becomes
\[\frac{df_v\left(v\right)}{dv}=4\pi \left(\frac{m}{2\pi kT}\right)^{3/2}v^2\mathrm{exp}\left(\frac{-mv^2}{2kT}\right) \nonumber \]
and the probability density becomes
\[\rho \left(v,\theta ,\varphi \right)= \left(\frac{m}{2\pi kT}\right)^{3/2}v^2\mathrm{exp}\left(\frac{-mv^2}{2kT}\right) \nonumber \]
This derivation can be recast as a computation of the expected value of the pressurepressure:expected value. To do so, we rephrase our description of the system: A molecule whose velocity components are \(\left(v^*,{\theta }^*,{\varphi }^*\right)\) creates a pressure \({2mv^*{\mathrm{cos} {\theta }^*\ }}/{At}\) on the area \(A\) with a probability of \(Av^*t\mathrm{cos} {\theta }^*/{V}\). (The latter term is the probability that a molecule, whose velocity is \(\left(v^*,{\theta }^*,{\varphi }^*\right)\), is, at time \(t=0\), in a location from which it can reach \(A\) within time \(t.\) If the molecule is to hit the wall within time \(t\), at time \(t=0\) the molecule must be within the tubular segment of volume is \(Av^*t\mathrm{cos} {\theta }^*\). The probability that the molecule is within this tubular segment is equal to the fraction of the total volume that this segment occupies.) Therefore, the product
\[\left(\frac{2mv^*\mathrm{cos} {\theta }^*}{At}\right)\left(\frac{Av^*t \mathrm{cos} {\theta }^*}{V}\right)=\frac{2m}{V} \left(v^* \mathrm{cos} {\theta }^* \right)^2 \nonumber \]
is the pressure contribution of a molecule with velocity \(\left(v^*,{\theta }^*,{\varphi }^*\right)\), when \({\theta }^*\) is in the interval \(0\le {\theta }^*<{\pi }/{2}\). The total pressure per molecule is the expected value of this pressure contribution; the expected value is the integral, over the entire volume of velocity space, of the pressure contribution times the probability density function for velocities.
It is useful to view the Maxwell-Boltzmann equation as the product of a term
\[\mathrm{exp}\left({-mv^2}/{2kT}\right) \nonumber \]
—called the Boltzmann factorBoltzmann factor—and a pre-exponential term that is proportional to the number of ways that a molecule can have a given velocity, \(v\). If there were no constraints on a molecule’s speed, we would expect that the number of molecules with speeds between \(v\) and \(v+dv\) would increase as \(v\) increases, because the probability that a molecule has a speed between \(v\) and \(v+dv\) is proportional to the volume in velocity space of a spherical shell of thickness \(dv\). The volume of a spherical shell of thickness \(dv\) is \(4\pi v^2dv\), which increases as the square of \(v\). However, the number of molecules with large values of \(v\) is constrained by the conservation of energy. Since the total energy of a collection of molecules is limited, only a small proportion of the molecules can have very large velocities. The Boltzmann factor introduces this constraint. A molecule whose mass is m and whose scalar velocity is \(v\) has kinetic energy \(\epsilon ={mv^2}/{2}\). The Boltzmann factor is often written as \(\mathrm{exp}\left({-\epsilon }/{kT}\right)\).


