2.12: Van der Waals' Equation
- Page ID
- 151663
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An equation due to van der Waals extends the ideal gas equation in a straightforward way. Van der Waals’ equation is
\[\left(P+\frac{an^2}{V^2}\right)\left(V-nb\right)=nRT \nonumber \]
It fits pressure-volume-temperature data for a real gas better than the ideal gas equation does. The improved fit is obtained by introducing two parameters (designated “\(a\)” and “\(b\)”) that must be determined experimentally for each gas. Van der Waals’ equation is particularly useful in our effort to understand the behavior of real gases, because it embodies a simple physical picture for the difference between a real gas and an ideal gas.
In deriving Boyle’s law from Newton’s laws, we assume that the gas molecules do not interact with one another. Simple arguments show that this can be only approximately true. Real gas molecules must interact with one another. At short distances they repel one another. At somewhat longer distances, they attract one another. The ideal gas equation can also be derived from the basic assumptions that we make in §10 by an application of the theory of statistical thermodynamics. By making different assumptions about molecular properties, we can apply statistical thermodynamics to derive\({}^{5}\) van der Waals’ equation. The required assumptions are that the molecules occupy a finite volume and that they attract one another with a force that varies as the inverse of a power of the distance between them. (The attractive force is usually assumed to be proportional to \(r^{-6}\).)
To recognize that real gas molecules both attract and repel one another, we need only remember that any gas can be liquefied by reducing its temperature and increasing the pressure applied to it. If we cool the liquid further, it freezes to a solid. Now, two distinguishing features of a solid are that it retains its shape and that it is almost incompressible. We attribute the incompressibility of a solid to repulsive forces between its constituent molecules; they have come so close to one another that repulsive forces between them have become important. To compress the solid, the molecules must be pushed still closer together, which requires inordinate force. On the other hand, if we throw an ice cube across the room, all of its constituent water molecules fly across the room together. Evidently, the water molecules in the solid are attracted to one another, otherwise they would all go their separate ways—throwing the ice cube would be like throwing a handful of dry sand. But water molecules are the same molecules whatever the temperature or pressure, so if there are forces of attraction and repulsion between them in the solid, these forces must be present in the liquid and gas phases also.
In the gas phase, molecules are far apart; in the liquid or the solid phase, they are packed together. At its boiling point, the volume of a liquid is much less than the volume of the gas from which it is condensed. At the freezing point, the volume of a solid is only slightly different from the volume of the liquid from which it is frozen, and it is certainly greater than zero. These commonplace observations are readily explained by supposing that any molecule has a characteristic volume. We can understand this, in turn, to be a consequence of the nature of the intermolecular forces; evidently, these forces become stronger as the distance between a pair of molecules decreases. Since a liquid or a solid occupies a definite volume, the repulsive force must increase more rapidly than the attractive force when the intermolecular distance is small. Often it is useful to talk about the molar volume of a condensed phase. By molar volume, we mean the volume of one mole of a pure substance. The molar volume of a condensed phase is determined by the intermolecular distance at which there is a balance between intermolecular forces of attraction and repulsion.
Evidently molecules are very close to one another in condensed phases. If we suppose that the empty spaces between molecules are negligible, the volume of a condensed phase is approximately equal to the number of molecules in the sample multiplied by the volume of a single molecule. Then the molar volume is Avogadro’s number times the volume occupied by one molecule. If we know the density, D, and the molar mass, \(\overline{M}\), we can find the molar volume, \(\overline{V}\), as
\[\overline{V}=\frac{\overline{M}}{D} \nonumber \]
The volume occupied by a molecule, V\({}_{molecule}\), becomes
\[V_{molecule}=\frac{\overline{V}}{\overline{N}} \nonumber \]
The pressure and volume appearing in van der Waals’ equation are the pressure and volume of the real gas. We can relate the terms in van der Waals’ equation to the ideal gas equation: It is useful to think of the terms \(\left(P+{{an}^2}/{V^2}\right)\) and \(\left(V-nb\right)\) as the pressure and volume of a hypothetical ideal gas. That is
\[ \begin{align*} P_{ideal\ gas}V_{ideal\ gas} &=\left(P_{real\ gas}+\frac{an^2}{V^2_{real\ gas}}\right)\left(V_{real\ gas}-nb\right) \\[4pt] &=nRT \end{align*} \nonumber \]
Then we have
\[V_{real\ gas}=V_{ideal\ gas}+nb \nonumber \]
We derive the ideal gas equation from a model in which the molecules are non-interacting point masses. So the volume of an ideal gas is the volume occupied by a gas whose individual molecules have zero volume. If the individual molecules of a real gas effectively occupy a volume \({b}/{\overline{N}}\), then \(n\) moles of them effectively occupy a volume
\[\left({b}/{\overline{N}}\right)\left(n\overline{N}\right)=nb. \nonumber \]
Van der Waals’ equation says that the volume of a real gas is the volume that would be occupied by non-interacting point masses, \(V_{ideal\ gas}\), plus the effective volume of the gas molecules themselves. (When data for real gas molecules are fit to the van der Waals’ equation, the value of \(b\) is usually somewhat greater than the volume estimated from the liquid density and molecular weight. See problem 24.)
Similarly, we have
\[P_{\text{real gas}}=P_{\text{ideal gas}}-\frac{an^2}{V^2_{\text{real gas}}} \nonumber \]
We can understand this as a logical consequence of attractive interactions between the molecules of the real gas. With \(a>0\), it says that the pressure of the real gas is less than the pressure of the hypothetical ideal gas, by an amount that is proportional to \({\left({n}/{V}\right)}^2\). The proportionality constant is \(a\). Since \({n}/{V}\) is the molar density (moles per unit volume) of the gas molecules, it is a measure of concentration. The number of collisions between molecules of the same kind is proportional to the square of their concentration. (We consider this point in more detail in Chapters 4 and 5.) So \({\left({n}/{V}\right)}^2\) is a measure of the frequency with which the real gas molecules come into close contact with one another. If they attract one another when they come close to one another, the effect of this attraction should be proportional to \({\left({n}/{V}\right)}^2\). So van der Waals’ equation is consistent with the idea that the pressure of a real gas is different from the pressure of the hypothetical ideal gas by an amount that is proportional to the frequency and strength of attractive interactions.
But why should attractive interactions have this effect; why should the pressure of the real gas be less than that of the hypothetical ideal gas? Perhaps the best way to develop a qualitative picture is to recognize that attractive intermolecular forces tend to cause the gas molecules to clump up. After all, it is these attractive forcesattractive force that cause the molecules to aggregate to a liquid at low temperatures. Above the boiling point, the ability of gas molecules to go their separate ways limits the effects of this tendency; however, even in the gas, the attractive forces must act in a way that tends to reduce the volume occupied by the molecules. Since the volume occupied by the gas is dictated by the size of the container—not by the properties of the gas itself—this clumping-up tendency finds expression as a decrease in pressure.
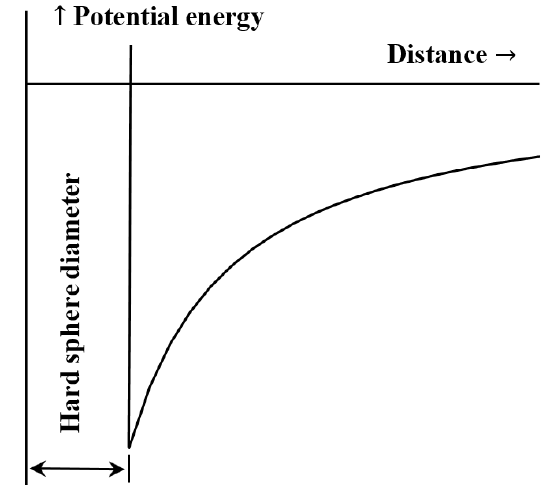
It is frequently useful to describe the interaction between particles or chemical moieties in terms of a potential energy versus distance diagram. The van der Waals’ equation corresponds to the case that the repulsive interaction between molecules is non-existent until the molecules come into contact. Once they come into contact, the energy required to move them still closer together becomes arbitrarily large. Often this is described by saying that they behave like “hard spheres”. The attractive force between two molecules decreases as the distance between them increases. When they are very far apart the attractive interaction is very small. We say that the energy of interaction is zero when the molecules are infinitely far apart. If we initially have two widely separated, stationary, mutually attracting molecules, they will spontaneously move toward one another, gaining kinetic energy as they go. Their potential energy decreases as they approach one another, reaching its smallest value when the molecules come into contact. Thus, van der Waals’ equation implies the potential energy versus distance diagram sketched in Figure 5.


