1.9: A Few Ideas from the Philosophy of Science
- Page ID
- 151659
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The goal of science is to create theories that accurately describe physical reality. In this book, we explore some of the most useful scientific theories that exist. They have been tested extensively. We know that there are limits to their applicability. We expect that further thought and experimentation will expand their scope. We expect that some elements of these theories will need to be modified in ways that we cannot anticipate, but we do not expect that the core concepts will be invalidated.
We love theories because they rationalize our environment. This is true not only of scientific theories but also of the panoply of conceptual frameworks that we use to organize our views about—and responses to— all of life’s issues. We are addicted to theories. We find nothing more disconcerting than information that we cannot put into a coherent context. Indeed, the term cognitive dissonance has entered the language to describe the feeling of disorientation that we experience when “things just don’t add up.”
Logically, confronted with a fact that contradicts one of our theories, we are compelled to give up the theory. We are not always logical. A fact that contradicts a pet theory is unlikely to be accepted at face value. We challenge it, as indeed we should. We scrutinize the offending fact and try to convince ourselves that it is no fact at all, merely a spurious artifact. Often, of course, this proves to be the case. Sometimes we conclude that the offending fact is spurious when it is not. We get stuffy about our theories. When we find one that suits us, we resist giving it up. It has been observed that a revolutionary scientific theory often achieves universal acceptance only after all those who grew up with the predecessor theory have died.
Science is ultimately a social enterprise. To develop and test theories about physical reality, participants in this enterprise must be in general agreement about the criteria that are to be applied. These criteria are frequently called “the philosophy of science.” To summarize the philosophy of science, we begin by observing that the goal of science is to explain the world that we experience through our sensory perceptions. It is easy to generate putative explanations that have little or no real value. Unfortunate experiences with past explanations have led to a broad consensus that scientific theories must have the following properties:
- operational definitions,
- logical structure,
- predictive capability and testability,
- internal consistency, and
- consistency with any and all experimental observations.
The theory must be about the properties of some set of things. By operational definitions, we mean that the subjects of the theory must measurable, and the theory must specify a set of operations for making each of these measurements. By logical structure, we mean that a satisfactory theory must include well-defined rules to specify how the subjects of the theory relate to one another. By predictive capability we mean that a satisfactory theory must be capable of predicting the results of experiments that have not been performed. By internal consistency we mean that a satisfactory theory must not allow us to logically derive contradictory conclusions, which also means that it must not predict more than one outcome for any particular experiment. Because a satisfactory theory makes predictions, it is also testable. It is possible to check whether the predictions correspond to reality. We require that the theory’s predictions be consistent with the results that we observe when we do the experiment.
The first four of these requirements really detail the characteristics that a theory must have in order to be considered a proper subject for scientific investigation. Only the last requirement speaks to the all-important issue of whether the theory accurately mirrors physical reality. We can never prove that any theory is true. What we can prove is that a theory fails to meet one of our criteria. Science progresses when we discover a fatal flaw in a currently accepted theory.
Let us think further about what we mean when we say that a theory must be a logical structure. Consider a simple classical syllogism.
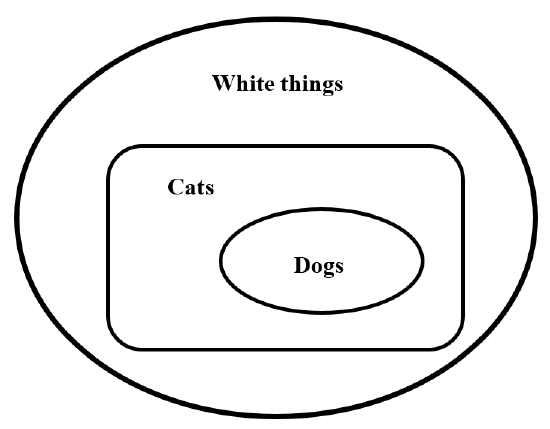
Major premise: All dogs are cats.
Minor premise: All cats are white.
Conclusion: All dogs are white.
As a logical structure, this seems to be satisfactory. We can represent the whole of its content in a simple diagram (See Figure 1), so if we want to view this syllogism as a theory about nature, its internal consistency is more or less self-evident. Moreover, viewed as a theory, it makes a prediction: All dogs are white. If we have operational definitions for “dog”, “cat”, and “white” that conform to customary usage, we can say that this syllogism meets our criteria for a proper subject for scientific investigation. Of course, as a mirror of reality, it fails.
To see the issue of logical structure from another perspective, let us consider the theory of evolution. Some people summarize the theory of evolution as teaching that the fittest individuals survive and defining survivors as those individuals who are most fit. They then point out that these are circular statements and proceed from this observation to the conclusion that the theory of evolution is devoid of real content. So it can be dismissed. Now, if we are not closed-minded about evolution, this analysis looks like a case of throwing out the baby with the bath water. Even so, we are likely to be troubled, because the circularity is undeniable. Does this circularity mean that the theory of evolution is bad science?
A tautology is a statement that must be true. Our analysis attempts to recast the entire content of the theory of evolution as one tautologous statement. If the whole of a theory is a single statement, and that statement must be true, then the theory cannot be tested. Our rules require that we reject it. However, our tautologous summary fails to capture the whole of the theory of evolution. If a theory that contains tautologous statements also makes predictions that are not tautologous, then it can be tested. In the present example, we can predict from the theory of evolution that selection of a particular trait through any process will cause increased expression of that trait in succeeding generations. Evolution is based on natural selection, but it postulates a mechanism that must be valid for any consistent selection process. It predicts that a farmer who selects for cows that produce more milk will eventually get cows that produce more milk. Thus, attempts to apply selective breeding are tests of the central element of the theory of evolution, and the success of selective breeding in every aspect of agriculture verifies a prediction of the theory.
There is no reason to object to a theory that has tautological elements so long as the content of the theory has real substance. What we require is that a theory’s predictions be non-trivial. We object when substantially all of a theory’s purported predictions are merely restatements of its premises, so that the whole of the theory is an exercise in verbiage.
We require scientific theories to be internally consistent. (Normally, we do not expect to be able to prove internal consistency. What we really mean is that we will discard any theory that we can show to be internally inconsistent.) The presence of tautologous statements cannot make a theory internally inconsistent. Indeed, we can expect any internally consistent theory to have tautological elements. After all, if we try to define all of the subjects of a theory, at least some of our definitions will inevitably be circular.
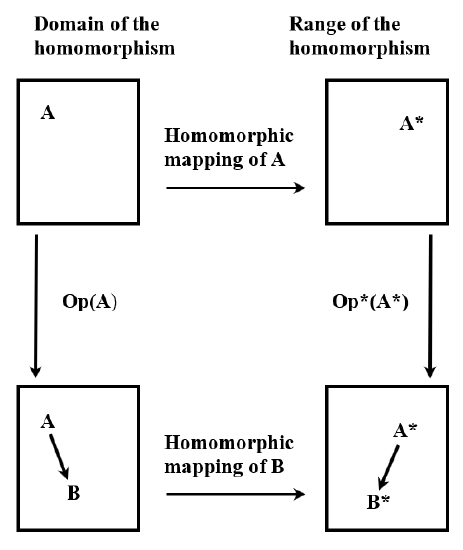
Another way to describe the logical structure of a physical theory is to say that a theory is a model for some observable part of the world. We want the model to include things and rules. The rules should specify how the things of the model change. When we talk about comparing predictions of the theory to the results of experiment, we mean that the changes that occur in the model when we apply the rules of the theory should parallel the changes that occur in the real world when we do the corresponding experiment. The idea is analogous to the mathematical concept of a homomorphism. A dictionary definition of a homomorphism\({}^{3}\) is “a mapping of a mathematical group, ring, or vector space onto another in such a way that the result obtained by applying an operation to elements of the domain is mapped onto the result of applying the same or a corresponding operation to their images in the range.” Stated more picturesquely, the idea of a homomorphism is that two mathematical structures have the same form: If one is “laid on top of the other”, there is a perfect correspondence between them. (See Figure 2.)
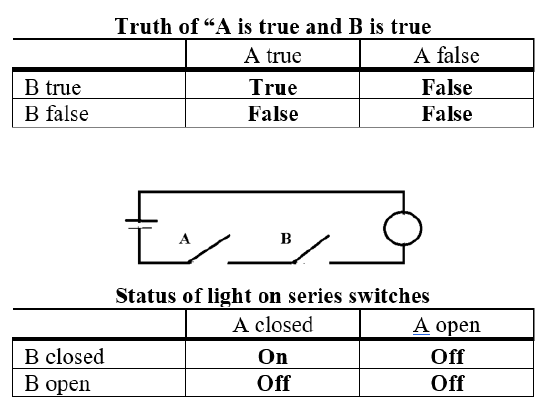
The idea of a one-to-one correspondence between two structures can be extended to the case where one structure is a logical structure and the other is a physical structure. Consider the logical structure, usually called a truth table, associated with the truth of the proposition “sentence A is true and sentence B is true.” The proposition is false unless both A and B are true. Now consider the performance of an electrical circuit that consists of a battery, switches A and B, and a light bulb, all connected in series. The light is off unless both A and B are on. There is a perfect correspondence between the elements of the logical structure and the performance of the circuit. (See Figure 3.) In fact, this is a special case of a much more extensive parallelism. For any sentence in propositional logic, there is a corresponding circuit—involving batteries, switches, and a light bulb—such that the bulb is on if the corresponding sentence is true and off if the sentence is false. Moreover, there is a mathematical structure, called Boolean algebra, which is homomorphic to propositional logic and exhibits the same parallelism to circuits. Digital computers carry this parallelism to structures of great complexity.
If we stretch our definition of a homomorphism to include comparisons of logical constructs with physical things, we can view a scientific theory as a logical construct that we are trying to make homomorphic with physical reality. We want our theory to map onto reality in such a way that changes in the logical construct map onto changes in physical reality. Of course, what we mean by this is the same thing we meant previously when we said that the predictions of our theory should agree with the results of experiment.
It is implicit in this view that any scientific theory describes an abstraction from reality. If, for example, we say that a physical system is at a particular temperature, this statement represents an approximation in at least two respects. First, we believe that we can measure temperature in continually more refined ways. If we know the temperature to six significant figures, this represents a very good approximation, but we believe that the “true” temperature can only be expressed using indeterminably many significant figures. To say that the temperature of the system has some value expressed to six significant figures is an approximation, albeit a very good one. Second, it is unlikely that all parts of any real system are actually at the same temperature. When we say that a physical system has a particular temperature, we mean that any differences in temperature between different parts of the system are too small to affect the behavior in which we are currently interested. In our discussions and deliberations about the physical system, we replace its actual properties by our best measurement. In doing so, we abstract something that we believe to be an essential feature from the reality we actually observe.
Implicit also is the idea that our theories about reality are subject to inevitable limitations. In the example above, any theory that, however accurately, predicts the single temperature that we use to describe the real system is inadequate to describe whatever small variations there may be from point to point within it. If we expand our theory to encompass variations over, say, distances of millimeters, then the expanded theory will be inadequate to describe variations over some smaller distance. Any “perfect” theory must exactly describe the motions of all of the system’s constituent particles. This is impossible not only because it conflicts with the basis premises of quantum mechanics, but also because it requires the theory to contain information at a level of detail equal to that in the physical system itself.
One way to express all of the same information at exactly the same level of detail is to have an exact replica of the system. This idea has been expressed by saying that an absolutely accurate map of Oklahoma City would have to be as large as Oklahoma City itself. For use as a map, such a thing would be useless. Similarly, a theory that predicts temperature is useful only if it predicts the temperature we measure (measurement being a part of the process by which we effect abstraction) experimentally. We can make use of multiple theories of the same phenomenon, if each of them has advantages and limitations that we recognize and respect. We see however, that in the end, there can be no single, all-encompassing theory. Any theory must model an approximation to reality. In the final analysis, reality is … reality.


