3.4: Variation of Surface Coverage with Temperature and Pressure
- Page ID
- 25376
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Application of the assumptions of the Langmuir Isotherm leads to readily derivable expressions for the pressure dependence of the surface coverage (see Sections 3.2 and 3.3) - in the case of a simple, reversible molecular adsorption process the expression is
\[ \theta = \dfrac{bP}{1+bP} \label{Eq1}\]
where \(b = b(T)\). This is illustrated in the graph below which shows the characteristic Langmuir variation of coverage with pressure for molecular adsorption.
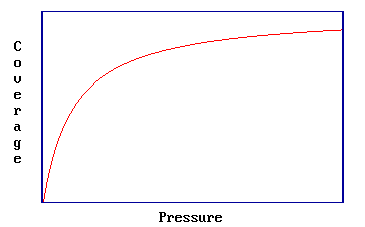
Note two extremes in Equation \(\ref{Eq1}\):
- At low pressures \[\lim_{P \rightarrow 0} θ = bP\]
- At high pressures \[\lim_{P \rightarrow \infty} θ = 1\]
At a given pressure the extent of adsorption is determined by the value of \(b\), which is dependent upon both the temperature (T) and the enthalpy (heat) of adsorption. Remember that the magnitude of the adsorption enthalpy (a negative quantity itself) reflects the strength of binding of the adsorbate to the substrate.
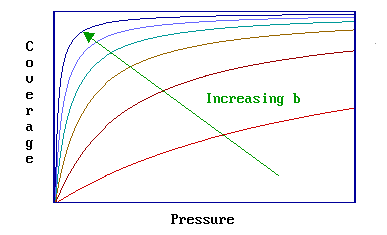
The value of \(b\) is increased by
- a reduction in the system temperature
- an increase in the strength of adsorption
Therefore the set of curves shown below illustrates the effect of either (i) increasing the magnitude of the adsorption enthalpy at a fixed temperature, or (ii) decreasing the temperature for a given adsorption system.
A given equilibrium surface coverage may be attainable at various combinations of pressure and temperature as highlighted below … note that as the temperature is lowered the pressure required to achieve a particular equilibrium surface coverage decreases.
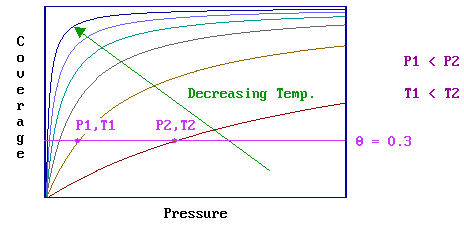
- this is often used as justification for one of the main ideologies of surface chemistry ; specifically, that it is possible to study technologically-important (high pressure / high temperature) surface processes within the low pressure environment of typical surface analysis systems by working at low temperatures. It must be recognized however that, at such low temperatures, kinetic restrictions that are not present at higher temperatures may become important.
If you wish to see how the various factors relating to the adsorption and desorption of molecules influence the surface coverage then try out the Interactive Demonstration of the Langmuir Isotherm (note - this is based on the derivation discuss previously ).
Determination of Enthalpies of Adsorption
It has been shown in previous sections how the value of b is dependent upon the enthalpy of adsorption. It has also just been demonstrated how the value of b influences the pressure/temperature (P-T) dependence of the surface coverage. The implication of this is that it must be possible to determine the enthalpy of adsorption for a particular adsorbate/substrate system by studying the P-T dependence of the surface coverage. Various methods based upon this idea have been developed for the determination of adsorption enthalpies - one method is outlined below:
Step 1: Involves determination of a number of adsorption isotherms, where a single isotherm is a coverage / pressure curve at a fixed temperature (Figure 3.4.1).
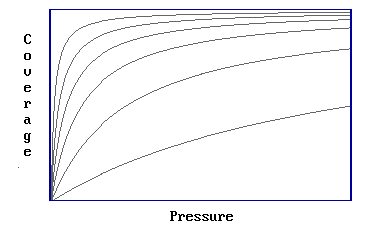
Figure 3.4.1
Step 2: It is then possible to read off a number of pairs of values of pressure and temperature which yield the same surface coverage (Figure 3.4.2)
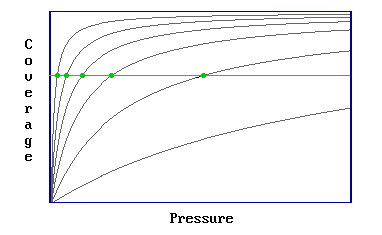
Figure 3.4.2:
Step 3: The Clausius-Clapeyron equation
\[ \left( \dfrac{\partial \ln P}{\partial \frac{1}{T}} \right)_{\theta} = \dfrac{\Delta H_{abs}}{R}\]
may then be applied to this set of (P-T) data and a plot of ( ln P ) v's (1/T) should give a straight line, the slope of which yields the adsorption enthalpy (Figure .
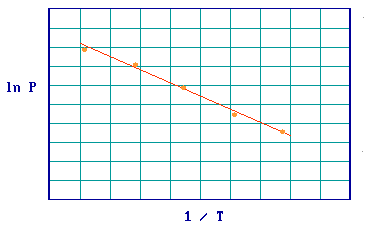
Figure 3.4.3:
The value obtained for the adsorption enthalpy is that pertaining at the surface coverage for which the P-T data was obtained, but steps 2 & 3 may be repeated for different surface coverages enabling the adsorption enthalpy to be determined over the whole range of coverages. This method is applicable only when the adsorption process is thermodynamically reversible.


