2.4: PE Curves and Energetics of Adsorption
- Page ID
- 25370
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section, we will consider both the energetics of adsorption and factors which influence the kinetics of adsorption by looking at the "potential energy diagram/curve" for the adsorption process. The potential energy curve for the adsorption process is a representation of the variation of the energy (PE or E) of the system as a function of the distance (\(d\)) of an adsorbate from a surface.
Within this simple one-dimensional (1D) model, the only variable is the distance (\(d\)) of the adsorbing molecule from the substrate surface.
Thus, the energy of the system is a function only of this variable i.e.
\[E = E(d)\]
It should be remembered that this is a very simplistic model which neglects many other parameters which influence the energy of the system (a single molecule approaching a clean surface), including for example
- the angular orientation of the molecule
- changes in the internal bond angles and bond lengths of the molecule
- the position of the molecule parallel to the surface plane
The interaction of a molecule with a given surface will also clearly be dependent upon the presence of any existing adsorbed species, whether these be surface impurities or simply pre-adsorbed molecules of the same type (in the latter case we are starting to consider the effect of surface coverage on the adsorption characteristics). Nevertheless, it is useful to first consider the interaction of an isolated molecule with a clean surface using the simple 1D model. For the purposes of this Module, we will also not be overly concerned whether the "energy" being referred to should strictly be the internal energy, the enthalpy or free energy of the system.
CASE I - Physisorption
In the case of pure physisorption, e.g., Ar/metals, the only attraction between the adsorbing species and the surface arises from weak, van der Waals forces. As illustrated below, these forces give rise to a shallow minimum in the PE curve at a relatively large distance from the surface (typically \(d > 0.3\, nm\)) before the strong repulsive forces arising from electron density overlap cause a rapid increase in the total energy.
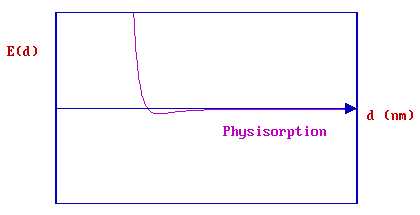
There is no barrier to prevent the atom or molecule which is approaching the surface from entering this physisorption well, i.e. the process is not activated and the kinetics of physisorption are invariably fast.
CASE II - Physisorption + Molecular Chemisorption
The weak physical adsorption forces and associated long-range attraction will be present to varying degrees in all adsorbate / substrate systems. However, in cases where chemical bond formation between the adsorbate and substrate can also occur, the PE curve is dominated by a much deeper chemisorption minimum at shorter values of d .
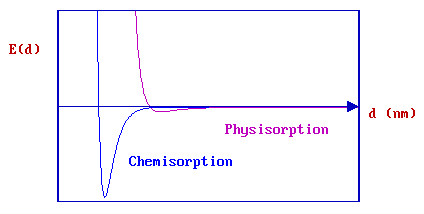
The graph above shows the PE curves due to physisorption and chemisorption separately - in practice, the PE curve for any real molecule capable of undergoing chemisorption is best described by a combination of the two curves, with a curve crossing at the point at which chemisorption forces begin to dominate over those arising from physisorption alone.
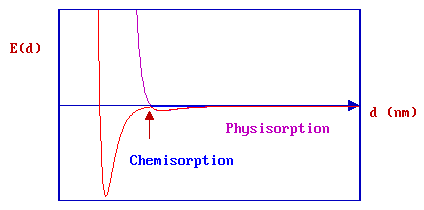
The minimum energy pathway obtained by combining the two PE curves is now highlighted in red. Any perturbation of the combined PE curve from the original, separate curves is most likely to be evident close to the highlighted crossing point.
For clarity, we will now consider only the overall PE curve:
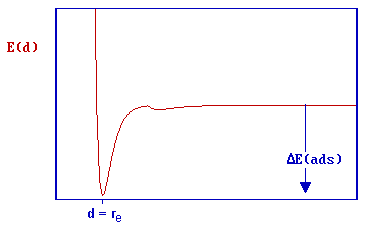
The depth of the chemisorption well is a measure of the strength of binding to the surface - in fact it is a direct representation of the energy of adsorption, whilst the location of the global minimum on the horizontal axis corresponds to the equilibrium bond distance (re ) for the adsorbed molecule on this surface.
The energy of adsorption is negative, and since it corresponds to the energy change upon adsorption it is better represented as ΔE(ads) or ΔEads . However, you will also often find the depth of this well associated with the enthalpy of adsorption, ΔH(ads).
The "heat of adsorption", Q, is taken to be a positive quantity equal in magnitude to the enthalpy of adsorption ; i.e. Q = -ΔH(ads) )
In this particular case, there is clearly no barrier to be overcome in the adsorption process and there is no activation energy of adsorption (i.e. Eaads = 0, but do remember the previously mentioned limitations of this simple 1D model). There is of course a significant barrier to the reverse, desorption process - the red arrow in the diagram below represents the activation energy for desorption.
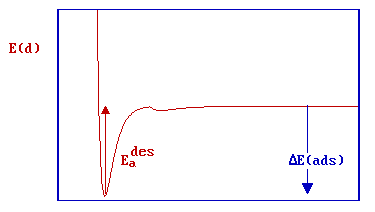
Clearly in this particular case, the magnitudes of the energy of adsorption and the activation energy for desorption can also be equated i.e.
\[E_a^{des} = ΔE (ads)\]
or
\[ E_a^{des} \approx -ΔH (ads)\]
CASE III - Physisorption + Dissociative Chemisorption
In this case the main differences arise from the substantial changes in the PE curve for the chemisorption process. Again, we start off with the basic PE curve for the physisorption process which represents how the molecule can weakly interact with the surface:
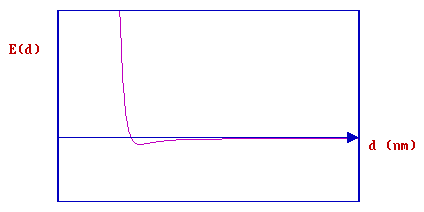
If we now consider a specific molecule such as H2 and initially treat it as being completely isolated from the surface ( i.e. when the distance, d, is very large ) then a substantial amount of energy has to be put into the system in order to cause dissociation of the molecule.
\[\ce{H_2 → H + H}\]
- this is the bond dissociation energy [ D(H-H) ], some 435 kJ mol-1 or 4.5 eV.
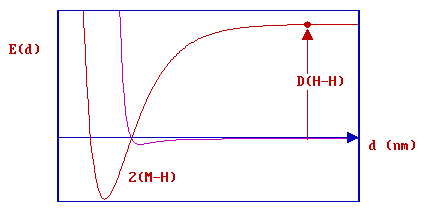
The red dot in the diagram above thus represents two hydrogen atoms, equidistant (and a long distance) from the surface and also now well separated from each other. If these atoms are then allowed to approach the surface they may ultimately both form strong chemical bonds to the substrate .... this corresponds to the minimum in the red curve which represents the chemisorption PE curve for the two H atoms.
In reality, of course, such a mechanism for dissociative hydrogen chemisorption is not practical - the energy downpayment associated with breaking the H-H bond is far too severe.
Instead, a hydrogen molecule will initially approach the surface along the physisorption curve. If it has sufficient energy it may pass straight into the chemisorption well ( "direct chemisorption" ) ....
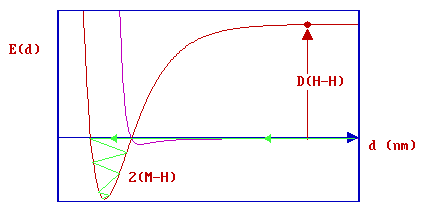
or, alternatively, it may first undergo transient physisorption - a state from which it can then either desorb back as a molecule into the gas phase or cross over the barrier into the dissociated, chemisorptive state (as illustrated schematically below).
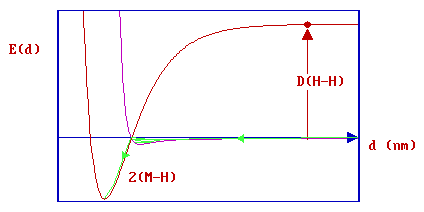
In this latter case, the molecule can be said to have undergone "precursor-mediated" chemisorption.
The characteristics of this type of dissociative adsorption process are clearly going to be strongly influenced by the position of the crossing point of the two curves (molecular physisorption v's dissociative chemisorption) - relatively small shifts in the position of either of the two curves can significantly alter the size of any barrier to chemisorption.
In the example immediately below there is no direct activation barrier to dissociative adsorption - the curve crossing is below the initial "zero energy" of the system.
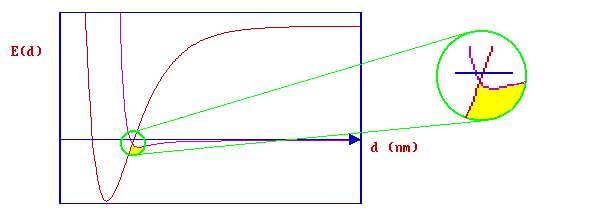
whilst, in this next case ….
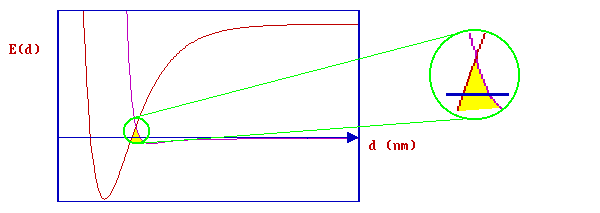
there is a substantial barrier to chemisorption. Such a barrier has a major influence on the kinetics of adsorption.
The depth of the physisorption well for the hydrogen molecule is actually very small (in some cases negligible), but this is not the case for other molecules and does not alter the basic conclusions regarding dissociative adsorption that result from this model; namely that the process may be either activated or non-activated depending on the exact location of the curve crossing.
At this point it is useful to return to consider the effect of such a barrier on the relationship between the activation energies for adsorption and desorption, and the energy (or enthalpy) of adsorption.
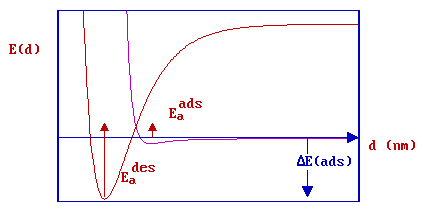
Clearly, from the diagram
\[E_a^{des} - E_a^{ads} = - ΔE_{ads}\]
but, since the activation energy for adsorption is nearly always very much smaller than that for desorption, and the difference between the energy and enthalpy of adsorption is also very small, it is still quite common to see the relationship
\[E_a^{des} \approx -ΔH_{ads}\]
For a slightly more detailed treatment of the adsorption process, you are referred to the following examples of More Complex PE Curves & Multi-Dimensional PE Surfaces.


