Hess's Law and Simple Enthalpy Calculations
- Page ID
- 3808
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Hess's Law is used to do some simple enthalpy change calculations involving enthalpy changes of reaction, formation and combustion. The enthalpy change accompanying a chemical change is independent of the route by which the chemical change occurs.
Hess's Law is the most important law in this part of chemistry and most calculations follow from it. Hess's Law is saying that if you convert reactants A into products B, the overall enthalpy change will be exactly the same whether you do it in one step or two steps or however many steps. If you look at the change on an enthalpy diagram, that is actually fairly obvious.
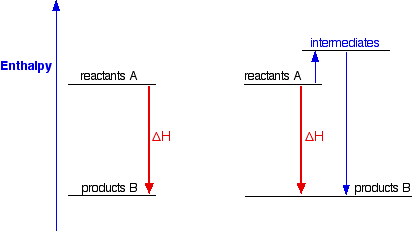
This shows the enthalpy changes for an exothermic reaction using two different ways of getting from reactants A to products B. In one case, you do a direct conversion; in the other, you use a two-step process involving some intermediates.
In either case, the overall enthalpy change must be the same, because it is governed by the relative positions of the reactants and products on the enthalpy diagram. If you go via the intermediates, you do have to put in some extra heat energy to start with, but you get it back again in the second stage of the reaction sequence. However many stages the reaction is done in, ultimately the overall enthalpy change will be the same, because the positions of the reactants and products on an enthalpy diagram will always be the same.
You can do calculations by setting them out as enthalpy diagrams as above, but there is a much simpler way of doing it which needs virtually no thought. You could set out the above diagram as:
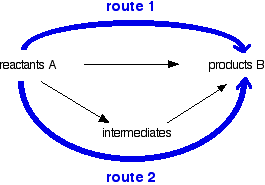
Hess's Law says that the overall enthalpy change in these two routes will be the same. That means that if you already know two of the values of enthalpy change for the three separate reactions shown on this diagram (the three black arrows), you can easily calculate the third - as you will see below. The big advantage of doing it this way is that you don't have to worry about the relative positions of everything on an enthalpy diagram. It is completely irrelevant whether a particular enthalpy change is positive or negative.
Although most calculations you will come across will fit into a triangular diagram like the above, you may also come across other slightly more complex cases needing more steps. You need to take care in choosing your two routes. The pattern will not always look like the one above.
Remember that that the standard enthalpy change of formation of benzene is impossible to measure directly. That is because carbon and hydrogen will not react to make benzene. Standard enthalpy changes of combustion, ΔH°c are relatively easy to measure. For benzene, carbon and hydrogen, these are:
| ΔH°c (kJ mol-1) | |
| C6H6(l) | -3267 |
| C(s) | -394 |
| H2(g) | -286 |
First you have to design your cycle.
- Write down the enthalpy change you want to find as a simple horizontal equation, and write ΔH over the top of the arrow. (In diagrams of this sort, we often miss off the standard symbol just to avoid clutter.)
- Then fit the other information you have onto the same diagram to make a Hess's Law cycle, writing the known enthalpy changes over the arrows for each of the other changes.
- Finally, find two routes around the diagram, always going with the flow of the various arrows. You must never have one of your route arrows going in the opposite direction to one of the equation arrows underneath it.
In this case, what we are trying to find is the standard enthalpy change of formation of benzene, so that equation goes horizontally.
You will notice that I haven't bothered to include the oxygen that the various things are burning in. The amount of oxygen is not critical because you just use an excess anyway, and including it really confuses the diagram.
Why have I drawn a box around the carbon dioxide and water at the bottom of the cycle? I tend to do this if I can't get all the arrows to point to exactly the right things. In this case, there is no obvious way of getting the arrow from the benzene to point at both the carbon dioxide and the water. Drawing the box is not essential - I just find that it helps me to see what is going on more easily.
Notice that you may have to multiply the figures you are using. For example, standard enthalpy changes of combustion start with 1 mole of the substance you are burning. In this case, the equations need you to burn 6 moles of carbon, and 3 moles of hydrogen molecules. Forgetting to do this is probably the most common mistake you are likely to make.
How were the two routes chosen? Remember that you have to go with the flow of the arrows. Choose your starting point as the corner that only has arrows leaving from it. Choose your end point as the corner which only has arrows arriving.
Now do the calculation: Hess's Law says that the enthalpy changes on the two routes are the same. That means that:
ΔH - 3267 = 6(-394) + 3(-286)
Rearranging and solving:
ΔH = 3267 + 6(-394) + 3(-286)
ΔH = +45 kJ mol-1
Working out an enthalpy change of reaction from enthalpy changes of formation
This is the commonest use of simple Hess's Law cycles that you are likely to come across.
Calculate the enthalpy change for the reaction between ethene and hydrogen chloride gases to make chloroethane gas from the standard enthalpy of formation values in the table. If you have never come across this reaction before, it makes no difference.
| ΔH°f (kJ mol-1) | |
| C2H4(g) | +52.2 |
| HCl(g) | -92.3 |
| C2H5Cl(g) | -109 |
In the cycle below, this reaction has been written horizontally, and the enthalpy of formation values added to complete the cycle.
Again, notice the box drawn around the elements at the bottom, because it is not possible to connect all the individual elements to the compounds they are forming in any tidy way. Be careful to count up all the atoms you need to use, and make sure they are written as they occur in the elements in their standard state. You mustn't, for example, write the hydrogens as 5H(g), because the standard state for hydrogen is H2.
And now the calculation. Just write down all the enthalpy changes which make up the two routes, and equate them.
+52.2 - 92.3 + ΔH = -109
Rearranging and solving:
ΔH = -52.2 + 92.3 - 109
ΔH = -68.9 kJ mol-1