Heat
- Page ID
- 1928
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Heat is the amount of energy that is transferred from one system to its surroundings because of a temperature difference.
History of Heat Transfer
In 1822, Jean-Baptiste Joseph Fourier founded the Fourier's law of heat transfer. He was able to come to this law through mathematical expressions and showed how heat conduction in bodies can be analyzed in mathematical series. The Fourier's Law of Heat Transfer states that the rate of heat conducted through a body is proportional to the negative temperature gradient in the body.
First Law of Thermodynamics
The First Law of Thermodynamics, also known as the Law of Conservation of Energy, states that the total energy remains constant between interactions of a system and its surroundings. Essentially, energy cannot be created or destroyed. A mathematical model of this is given below.
\[q_{System}+q_{Surroundings} = 0\]
When two systems, or bodies, are brought together, heat, as energy, will transfer from the hotter body to the colder body. As a result, molecules of the hotter body loses kinetic energy to the colder body. This then results in the flow of heat between the bodies, the colder body will increase in temperature and the hotter body will decrease in temperature.
The factors that the quantity of heat needed to change the temperature of a substance depend on:
- The amount of temperature change
- The quantity of substance
- The type of substance
- Components: type of atoms/molecules
Phase Changes and Heat
First, heat causes a difference in temperature when heat flows from one body to another. Heat transfer can also cause a change in the state of matter. For example, heating H2O(s) (ice) would cause the molecules to move at a faster rate. The increase in rate would break intermolecular forces and cause the solid to change phase into a liquid, where the intermolecular forces aren't as strong and constricting as those in a solid.
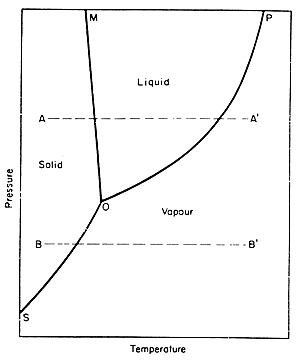
One can also look at phase diagrams to see how heat and pressure affect the changes in phases. A phase diagram is a graphical representation of the conditions of temperature and pressure at which solids, liquids, and gases exist, either as single phases, or states of matter or as two or more phases in equilibrium with one another. The following picture is the example of a phase diagram:
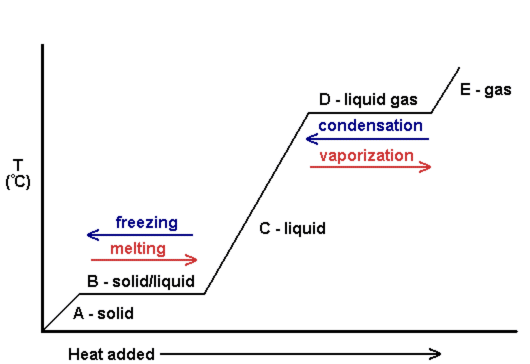
One can also look at heating curves to see the change in temperature as more heat is added. The following is an example of a heating curve. Notice that as the phase changes occur, there is no change in temperature.
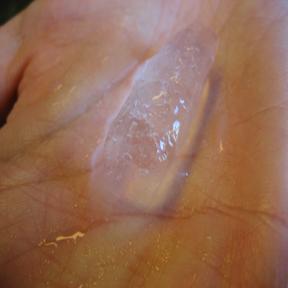
Visual Examples of Heat
In the above example, the left picture shows solid ice that has been kept at low temperatures. The middle picture shows ice absorbing heat from its surroundings and proceeding through the phase change from solid to liquid. The right picture successfully shows the complete absorption of the heat from the surroundings, melting until all of the ice has become liquid. The darker color underneath the middle of the location of the ice in the second picture indicates the presence of liquid water.


The left picture shows solid ice that has been kept at low temperatures being kept in a hand. The middle picture shows the ice that has been in a person's hand for a short period of time and is going through the phase change from solid to liquid. The right picture clearly shows that after the removal of ice, only liquid water is present in the hand.
Units of Heat
The calorie is the amount of heat needed to change the temperature of 1g of water by 1 degree Celsius. The kilocalorie (1 kCal = 1000 cal) is the unit of heat that we usually encounter in daily life, such as on the back of a cereal box. Note that calories are denoted by a lowercase "c" and kilocalories are denoted by and uppercase "C".
The calorie is also related to the SI energy unit, joule.
1 cal = 4.184 Joules
The British Thermal Unit (BTU) is also used to define the amount of heat needed to raise one pound of water one degree Fahrenheit.
1 BTU = 252 calories = 1055 Joules
Heat Capacity
The heat capacity is the amount of heat, expressed usually in Joules or calories, needed to change the system by 1 degree Celsius. The specific heat capacity is the amount of heat required to raise 1 gram of a substance by 1 degree Celsius.
For example, the specific heat of H2O(l) is 4.18 J/g ° C.
- \(C_p\) denotes the specific heat capacity for specific heat capacity at constant pressure.
- \(C_v\) denotes the specific heat capacity for specific heat capacity at constant volume.
Calculating the Amount of Heat
In order to calculate the amount of heat necessary to raise something by a certain temperature change, we will need certain information.
- Temperature Change
- Amount of Substance (only for use with Cp or Cv)
- Usually given in grams or moles of substance.
- Specific Heat Capacity or Heat Capacity
We can now use the following formula to solve for the amount of heat needed.
\[q = m \, C_p \, \Delta{T}\]
or
\[q = C_p \Delta{T}\]
Where,
- \(q\) = Quantity of Heat
- \(m\) = Mass of Substance
- \(\Delta{T}\) = Change in Temperature
- \(C_p\) = Specific/Molar Heat Capacity
- \(C\) = Heat Capacity (Not Dependent on Mass)
Remember that you don't always have to use the specific or molar heat capacities. One can use a normal heat capacity to find the energy, in which case the amount of substance isn't necessary information. This is when you would use the second equation.
Given 500 g H2O(l), how much heat is required to raise the temperature of H2O(l) from 8 °C to 88°C?
- Answer
-
Answers are in the attached files section.
References
- Bindel, T. H., Fochi, J. C. "Guided Discovery: Law of Specific Heats." J. Chem. Educ. 1997: 74, 955.
- Kimbrough, Doris R. "Heat Capacity, Body Temperature, and Hypothermia." J. Chem. Educ. 1998: 75, 48.
- Petrucci, et al. General Chemistry Principles & Modern Applications. 9th ed. Upper Saddle River, NJ: Pearson Prentice Hall, 2007
- Engel, et al. Physical Chemistry for the Life Sciences. Upper Saddle River, NJ: Pearson Prentice Hall, 2008
- Smith, E.Brian. Basic Chemical Thermodynamics. 5th ed. London: Imperial College Press, 2004
- Stolen, et al. Chemical Thermodynamics of Materials Macroscopic and Microscopic Aspects. West Sussex, England: John Wiley & Sons Ltd, 2004
- "heat." Encyclopædia Britannica. 2008. Encyclopædia Britannica Online. 31 May 2008
- "specific heat." Encyclopædia Britannica. 2008. Encyclopædia Britannica Online. 31 May 2008
- "British thermal unit." Encyclopædia Britannica. 2008. Encyclopædia Britannica Online. 31 May 2008
- "Heat Transfer," Microsoft® Encarta® Online Encyclopedia 2008 uk.encarta.msn.com © 1997-2008
- AP HS Chemistry. Web. 11 Mar. 2010. http://aphschem.blogspot.com/2009/10...curve-lab.html Unit Operations in Food Processing - R. L. Earle." NZIFST - The New Zealand Institute of Food Science and Technology. Web. 11 Mar. 2010. <www.nzifst.org.nz/unitoperations/drying1.htm>
Contributors
- Katrina Lau (UCD)




