Trouton's rule
- Page ID
- 80098
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Trouton's rule says that for many (but not all) liquids, the entropy of vaporization is approximately the same at ~85 J mol−1K−1. The (partial) success of the rule is due to the fact that the entropy of a gas is considerably larger than that of any liquid.
\[S_{gas} \gg S_{liquid}\]
Therefore, the entropy of the initial state (e.g. the liquid) is negligible in determining the entropy of vaporization
\[\Delta S_{vap}= S_{gas} - S_{liquid} \approx S_{gas} \label{approx}\]
When a liquid vaporizes its entropy goes from a modest value to a significantly larger one. This is related to the ratio of the enthalpy of vaporization and the temperature of the transition:
\[ΔS_{vap}= \dfrac{ΔH_{vap}}{T} \label{Eq1}\]
\(ΔS_{vap}\) is found to be approximately constant at the boiling point (Figure \(\PageIndex{1}\)):
\[ΔS_{vap} \approx 85 \,J\, mol^{−1}K^{−1} \label{Trule}\]
This is Trouton’s rule, which is valid for many liquids (e.g, the entropy of vaporization of toluene is 87.30 J K−1 mol−1, that of benzene is 89.45 J K−1 mol−1, and that of chloroform is 87.92 J K−1 mol−1). Because of its convenience, the rule is used to estimate the enthalpy of vaporization of liquids whose boiling points are known.
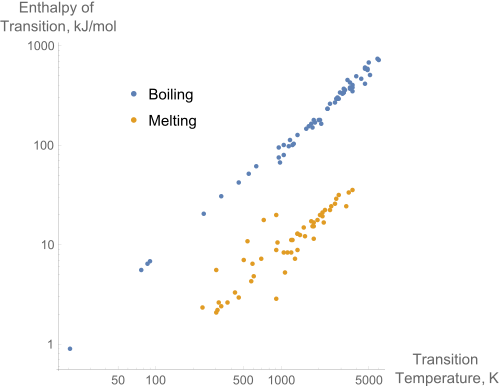
Trouton’s rule can be used to estimate the enthalpy of vaporization of liquids whose boiling points are known.
Experimental values vary rather more than this and for gases such as neon, nitrogen, oxygen and methane whose liquids all boil below 150 K, have values that are in the range 65−75, benzene, many 'normal' liquids and liquid sodium, lithium and iodine, in the range 80−90 and ethanol, water, hydrogen fluoride in the range 105−115 J mol−1 K−1. Thus is nothing unusual about 150 K, but rather an influence from intermolecular interactions.
The value of ~85 J mol−1K−1 corresponds to a interaction energy of ~9.5kT per molecule and so the boiling point gives an indication of the strength of the cohesive energy holding molecules together in the condensed phase. When the cohesive energy exceeds this value, as in water, then the ratio \(ΔH_{vap}/T\) (Equation \(\ref{Eq1}\)) is larger and conversely the ratio is smaller when the cohesive energy is less as in Neon or methane. The ≈9.5kT minimum energy per molecule is quite a modest energy; if a molecule has six near neighbors this corresponds to about 3kT/2 per interaction between two molecules, roughly the average thermal energy.
There is no universal rule for the entropy of melting since a similar approximate like that used for Trouton's law (Equation \(\ref{approx}\)) does not exist. However, if the mature of the interactions are consistent between a set of solids, then a crude correlation can be identified (Figure \(\PageIndex{1}\); orange symbols).
Trouton Rule's does not Apply to Structured Liquids
For example, the entropies of vaporization of water, ethanol, formic acid and hydrogen fluoride are far from the predicted values. However, if the liquid presents hydrogen bonding or any other kind of high ordered structure, its entropy will be particularly low and the entropy gain during vaporization will greater, too. The enthalpy of vaporization is greater for hydrogen-bonding molecules than for plain alkanes. For low-molecular weight alcohols, this effect is pronounced. The longer the alkane chain becomes, the more the compound behaves like a pure alkane.
| Liquid | \(\Delta H_{vap}\) (kJ/mol) | \(\Delta H_{vap}\) (kJ/mol per carbon) |
|---|---|---|
| Methanol | 38 | 38 |
| Ethanol | 42 | 21 |
| n-propanol | 47 | 16 |
| n-butanol | 52 | 13 |
| n-pentanol | 57 | 11 |
| n-hexanol | 61 | 10 |
| n-heptanol | 67 | 10 |
| n-octanol | 71 | 9 |
| n-nonanol | 77 | 9 |
| n-decanol | 82 | 8 |
| Data obtained from the NIST Webbook. | ||
Keeping in mind the relative molecular weights of the compounds, you can see there is a decreasing effect of the hydrogen bonding (and other) effects on the n-alcohol series as we move to larger chains and become less alcohol-like (structured liquid) and more alkane-like (unstructure liquid). This is much more obvious when \(\mathrm{\Delta}H\) is normalized to a per-carbon basis.
Table \(\PageIndex{1}\) shows that two different processes control the enthalpy of vaporization, and similarly the saturation vapor concentration (also known as vapor pressure) or boiling point. At the low-molecular weight end, hydrogen bonding dominates, so we see the behavior common to polar, hydrogen-bonding compounds. At the high-molecular weight end, we see the pattern observed for alkanes.
Trouton's rule hardly works for high ordered substances exhibiting hydrogen bonding. Other factors like the enthalpy of vaporization for a long chained organic molecule {strength of Van der Waals forces} may also play some significance role.
The experimentally determined enthalpy of vaporization if water is \(40.7\, kJ\,mol^{-1}\). Does water follow Trouton's rule in predicting the enthalpy of vaporization?
Solution
From Equations \(\ref{Eq1}\) and \(\ref{Trule}\), we get
\[ΔS_{vap}= \dfrac{\Delta H_{vap}}{T} \approx 85 \, J \,K^{-1} mol^{-1}\nonumber\]
This predicts that (since water boils at 373.15 K under atmospheric pressure)
\[ΔH_{vap} \approx (85 \, J \,K^{-1} mol^{-1} )( 373.15\, K) = 31.7\, kJ \,K^{-1} mol^{-1} \nonumber\]
This deviates from the observed enthalpy change of \(40.7\, J\, K^{-1} mol^{-1}\) by 23%, which is a sizable deviation from experiment. So, Trouton's law does not apply to water.
This deviation is similarly observed by comparing the determined entropy of vaporization (Equation \(\ref{Eq1}\)) to the estimate from Trouton's law
\[ΔS_{vap} = \dfrac{40.7\, kJ\, mol^{-1}}{373.15 K} = 109.1 J\, K^{-1} mol^{-1} > 85 \, J \,K^{-1} mol^{-1} \nonumber \]
Example \(\PageIndex{1}\) demostrates the general observation that the \(S_{liquid}\) for structured liquids is lower than for unstructured liquids, so the entropy gain during vaporization (i.e., \(\Delta_{vap}\) in Equation \(\ref{approx}\)) will be greater.
Trouton Rule's does not Apply to Ordered Gasses
In contrast to water, the entropy of vaporization of formic acid has negative deviance from Trouton's rule. This fact indicates the existence of an orderly structure in the gas phase; it is known that formic acid forms a dimer structure even in the gas phase (Figure \(\PageIndex{2}\)). As with water, where hydrogen bonding results in structured phase and reduced entropy of the liquid (positive deviation from Trouton's law), the dimerization in formic acid reduces the entropy of the gas (negative deviation from Trouton's law).

Negative deviance can also occur as a result of a reduced gas phase entropy owing to a low population of excited rotational states in the gas phase, particularly in small molecules such as methane. Trouton's rule validity can be increased by considering
\[\Delta {\bar {S}}_{vap}=4.5R+R\ln T\]
Contributors and Attributions
- Renato at Chemistry StackExchange
- PHANUEL ALUOMU at Chemistry StackExchange
- porphyrin at Chemistry StackExchange
- airhuff at Chemistry StackExchange
- Wikipedia

