Reversibility and Le Chatelier
- Page ID
- 4270
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\(\newcommand{\ket}[1]{\left| #1 \right>} \)
\( \newcommand{\bra}[1]{\left< #1 \right|} \)
\( \newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>} \)
\( \newcommand{\qmvec}[1]{\mathbf{\vec{#1}}} \)
\( \newcommand{\op}[1]{\hat{\mathbf{#1}}}\)
\( \newcommand{\expect}[1]{\langle #1 \rangle}\)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Sometimes, there is not a big difference in energy between reactants and products of a reaction. What happens then? Does the reaction go forward, because it will not cost a lot of energy? Or does it not proceed, because there isn't enough driving force? For example, one simple reaction that occurs all the time is the reaction of water with carbon dioxide. This is a reaction that happens when carbon dioxide dissolves in lakes, rivers and oceans. It even happens in your own bloodstream.

Water reacts with carbon dioxide to form carbonic acid. However, carbonic acid also decomposes spontaneously in water. It reacts to form carbon dioxide and water.
In other words, this is a reaction that can go either direction. It can go forwards or backwards. It is an example of an equilibrium reaction. An equilibrium reaction is one that is energetically balanced, so that it really isn't favored to go in either direction. Equilibrium reactions are extremely important in nature, partly because of the forward and reverse capabilities that they offer. In essence, they are reactions with an "undo" button. The reaction can proceed in one direction when needed, and it can proceed in the other direction when needed.
However, there are some inherent limitations involved. Frequently, equilibrium reactions only proceed "partway". That is, a group of molecules will start to produce products. However, at some point those products will begin reverting to the starting materials again. Eventually the system will settle out as a mixture of reactants and products.
What if it's really important that we have the products of the reaction at one point, with none of the reactants? And if later on we need the reactants, but not any of the products? It would be useful if there were a way to control the direction of an equilibrium reaction, so that we could "push" it to one side or the other.
Control of equilibrium reactions can be remarkably simple. It follows a rule that was observed by Henri le Châtelier (ah-REE luh shah-tell-YAY), a French industrial chemist, around 1900. Le Chatelier noticed that equilibrium reactions often shift direction if the conditions of the reaction are changed. In general, adding any product of the reaction shifts the balance back toward the reactants. If any product of the reaction is added, the reaction makes more starting materials. Thus, adding more carbonic acid to a carbon dioxide - water - carbonic acid mixture would result in reverse reaction, producing more water and carbon dioxide. Adding more carbon dioxide, on the other hand, would lead to production of more carbonic acid.
Here is a cartoon illustration of "le Châtelier's Principle" at work. Suppose red squares and blue ovals can react together to make black circles and green circles. Maybe there is a natural equilibrium in this reaction, so that the two piles of shapes are roughly equal in size.

What would happen if something knocked this system off balance? For example, maybe black circles are highly elusive, and they just wander away as soon as they are formed. The system won't be in equilibrium anymore, because without those black circles, the balance will be upset, with not enough things on the right side for the number of things on the left.

Le Chatelier noticed that nature automatically corrects for such changes. If some of the black circles disappear, the reaction will kick into action again, using up some red squares and blue ellipses to produce more green and black circles. The exact numbers of shapes won't return to exactly the same as before, because some of the black circles have still gone missing, but the system will have shifted to use up more reactants on the left and to produce more products on the right, so that the overall ratio between right and left is restored.
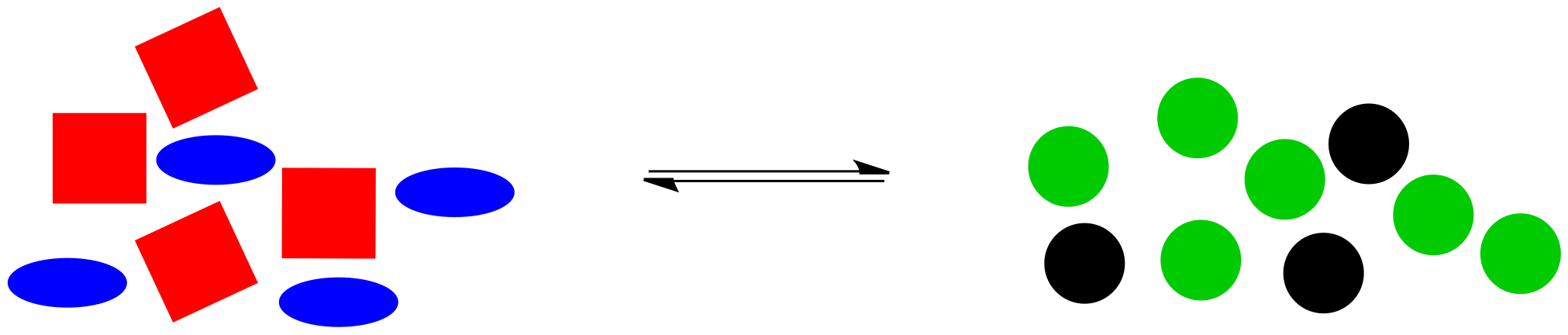
Alternatively, maybe we found a way to make the black circles stay where they are. Instead, we have dumped in a bunch of extra blue ellipses. Once again, the system is knocked off balance. This time, there is too much stuff on the left, compared to the amount on the right side.

The reaction goes into action again. It uses up some of those extra blue ellipses (and, at the same time, some of the red squares) to produce more black and green circles, bringing the system back to the original ratio of right side shapes to left side shapes.

In general, if molecules are added to a system, the reaction will shift to bring the system back into equilibrium. If molecules are removed from the system, the reaction will also shift to bring the system back into equilibrium. Furthermore, because heat can be consumed by (or produced by) reactions, temperature can sometimes be used to shift equilibria. If a reaction is exothermic, heat is a product of the reaction. Adding more heat will result in the reaction shifting to produce more reactants. Cooling the reaction (removing heat) would do the opposite: the reaction would shift to produce more heat, and more products.
In the cartoon, we have a shape-shifting reaction again, but this time the reaction releases energy (those are orange flames, symbolic of the heat produced).

What happens if that energy is removed? For example, if heat is removed through addition of a pale blue ice cube, what will be the effect on the system?

Those orange energy shapes (the "flames") were a part of the system. If they are removed, the system will have to shift in order to restore them. If the reaction pushes to the right again, more energy will be released, bringing the system back into equilibrium.

Contributors and Attributions
Chris P Schaller, Ph.D., (College of Saint Benedict / Saint John's University)


