Bond Energies
- Page ID
- 22757
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Bond energies are limited in their application for the reasons discussed earlier. They were:
- values are for gases only
- many values are averages
These are serious drawbacks if you want energy information about most reactions. Fortunately there is another way. Remember in our definition of enthalpy (\(H\)) we said it was a "state function". The net enthalpy change (\(ΔH\) --which is the only kind of enthalpy quantity we can measure) is independent of path. What does this mean?
If a process can be carried out in a single step, the enthalpy change for that step will be the same as for a series of steps which add up to give the same overall step.
The diagram shows two possible pathways for one reaction:

The direct reaction of the elements nitrogen and oxygen in a 1:2 molar ratio will produce 2 moles of nitrogen dioxide and absorb 68 kJ. But it is also possible to begin with the same elements under different conditions (like a 1:1 molar ratio) and produce 2 moles of nitrogen monoxide. This process absorbs 180 kJ.
The nitrogen monoxide can then react with additional oxygen to form 2 moles of nitrogen dioxide. This process releases 112 kJ.
The sum of the two reactions involving nitrogen monoxide gives the production of nitrogen dioxide:
\[180 \;kJ + N_2 + O-2 \rightarrow 2 NO\]
\[\underline{2 NO + O_2 \rightarrow 2 NO_2 + 112\; kJ}\]
\[68 \;kJ + N_2 + 2 O_2 \rightarrow 2 NO_2\]And because that is true, the enthalpy changes are also additive:
\[180 \;kJ + (-112\; kJ) = 68\; kJ\]
So with a sufficiently ambitious catalog of reaction enthalpy changes it is sometimes possible to calculate--rather than measure--the enthalpy change for a new reaction.
Give the following data:
\[ H_2 + ½ O_2 \rightarrow H_2O + 286\; kJ\]
\[N_2O_5 + H_2O \rightarrow 2HNO_3 + 77 \; kJ\]
\[N_2 + 3O_2 + H_2 \rightarrow 2HNO_3 + 348 \; kJ\]
Calculate \(\Delta{H_{rxn}}\) for
\[2N_2 + 5O_2 \rightarrow 2N_2O_5\]
Solution
To begin these problems, concentrate on the items in the balanced equation you want. Where are they found in the data available?
\[ H_2 + ½ O_2 \rightarrow H_2O + 286\; kJ\]
\[\color{red} N_2O_5 \color{black} + H_2O \rightarrow 2HNO_3 + 77 \; kJ\]
\[ \color{red} N_2 \color{black} + \color{red} 3O_2 \color{black} + H_2 \rightarrow 2HNO_3 + 348 \; kJ\]
Once these are located, the equations needs to be adjusted so that the substances appear in the same amount as in the desired reaction and on the same sides.
\[ H_2 + ½ O_2 \rightarrow H_2O + 286\; kJ\]
\[2 \times (2 HNO_3 + 77\; kJ \rightarrow \color{red} N_2O_5 \color{black} + 2 H_2O)\]
\[2 \times (\color{red}N_2 \color{black} + \color{red} 3 O_2 \color{black} + H_2 \rightarrow 2 HNO_3 + 348 \; kJ)\]
Notice that this procedure did not fix the \(O_2\) entirely. However, there are also things that we need to get rid of so that the equations will add up to give the desired reaction of \(H_2\), \(H_2O\), and \(HNO_3\). If the first reaction is reversed and doubles, this will happen:
\[ 2 \times ( H_2O + 572\; kJ \rightarrow 2 H_2 + O_2)\]
\[2 \times (2 HNO_3 + 77\; kJ \rightarrow \color{red} N_2O_5 \color{black} + 2 H_2O\]
\[2 \times (\color{red}N_2 \color{black} + \color{red} 3 O_2 \color{black} + H_2 \rightarrow 2 HNO_3 + 348 \; kJ)\]
Multiply all this out to get
\[ {2 H_2O} + 572\; kJ \rightarrow \cancel{2 H_2} + {O_2}\]
\[{4 HNO_3} + 154\; kJ \rightarrow 2 \color{red} N_2O_5 \color{black} + 2 H_2O\]
\[2 \color{red} N_2 \color{black} + \color{red} O_2 \color{black} + 2 H_2 \rightarrow 4 HNO_3 + 696 \; kJ\]
Then we add and simplify, much like we do with a series of half reactions
\[ \cancel{2 H_2O} + 572\; kJ \rightarrow \cancel{2 H_2} + \cancel{O_2}\]
\[\cancel{4 HNO_3} + 154\; kJ \rightarrow 2 \color{red} N_2O_5 \color{black} + \cancel{2 H_2O}\]
\[\underline {2 \color{red} N_2 \color{black} + \cancel{6} \color{red} O_2 \color{black} + \cancel{2 H_2} \rightarrow \cancel{4 HNO_3} + 696 \; kJ}\]
\[ 30 \;kJ + 2 N_2 + 5 O_2 \rightarrow 2N_2O_5\]
So what's the advantage? Theoretically every reaction can be "rewritten" as a series of processes involving elements forming individual compounds. It does not matter whether the reaction actually occurs that way, of course, because the enthalpies are additive (Hess's Law). The heats of formation represent those reactions and therefore can be used in their place to determine the overall enthalpy change in a reaction based on a mathematical statement.
This additivity of heats of reaction (or reaction enthalpies) is generally known as Hess's Law. But it is also possible to state the equivalent of Hess's Law in purely mathematical terms with the introduction of an additional concept: standard enthalpy of formation.
If elements in their standard states (normal atmospheric pressure) and \(25^oC\) are defined as having no enthalpy of formation (i.e., it takes no energy to get an element the way it would normally be), then all compounds will have some enthalpy change associated with their formation from those elements.
For example, when liquid water is formed from gaseous hydrogen and oxygen, we can write the following thermochemical equation:
\[H_2 + ½ O_2 \rightarrow H_2O\; + \;285.8\; kJ\]
The 285.8 kJ is the enthalpy of formation for liquid water: the energy released when one mole of liquid water forms from its elements.
The fact that the value is on the products side of the reaction shows this is an exothermic process. The value can also be written separately (as in a table). By convention, a negative sign is then applied to show that there is a net loss of enthalpy in the system as the reactants become products. That means heat is released to the surroundings. So we can say \(ΔH_f^o = -285.8\; kJ/mol\) of water. All kinds of enthalpies of formation have been tabulated (Table T1).
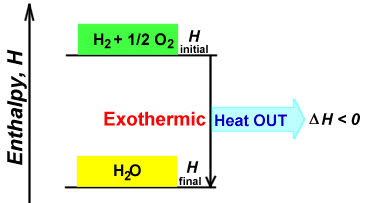
For an endothermic reaction the enthalpy of reaction would be written on the reactant side:
\[177.8 kJ \;+ \;CaCO_3 \rightarrow CaO + CO_2\]
And when written in a table, the value would be \(ΔH_{rxn} = +177.8\; kJ/mol\). All "heats of reaction" are molar and therefore proportional. Stoichiometric amounts of heat can be determined for a given amount of starting material just as any other stoichiometric calculation would be done.
The thermochemical equation for the acid/base neutralization reaction of hydrochloric acid with barium hydroxide solution is
\[ 2HCl + Ba(OH)_2 \rightarrow BaCl_2 + 2 H_2O + 118 \; kJ\]
How much heat is produces if 34.5 g of HCl reacts with a stoichiometric amount of Barium hydroxide?
Solution
Step 1: Balance the Equation
Given and confirmed
Step 2: Find number of moles of
\[ (34.5\; g) \times \dfrac{1 \; mol}{36.5\; g} = 0.945 \; mol \; HCl\]
Step 3: Use ration to find kJ
\[ (0.945 \;mol\; HCl) \times \dfrac{118\; kJ}{2 \; mol \;HCl} = 55.8 \; kJ\]
So what's the advantage? Theoretically every reaction can be "rewritten" as a series of processes involving elements forming individual compounds. It does not matter whether the reaction actually occurs that way, of course, because the enthalpies are additive (Hess's Law). The heats of formation represent those reactions and therefore can be used in their place to determine the overall enthalpy change in a reaction based on a mathematical statement.
\[\sum{ΔH^o_{f\;products}} - \sum{ΔH^o_{f\;reactants}}= ΔH_{rxn}\]
That looks fearsome but it simply says that the overall enthalpy change for a reaction is the difference between the heat content of the products and the heat content of the reactants. If the products end up with more stored energy than the reactants, the enthalpy change will be positive (endothermic). If the products end up with less stored energy than the reactants, the enthalpy change will be negative (exothermic).
Thermite is a generic term for a mixture of metal and metal oxide used to generate tremendous heat. During the reaction one metal is reduced and the other is oxidized. The classic thermite mixture consists of iron(III) oxide and aluminum:
\[Fe_2O_3 + 2 Al \rightarrow Al_2O_3 + 2 Fe\]- The heat of formation for iron(III) oxide is -826 kJ/mol.
- The heat of formation for aluminum oxide is -1676 kJ/mol.
How much energy is released in this reaction?
Solution
\[ΔH_{rxn} = -1676\; kJ - (-826 \;kJ) = -850 \;\text{kJ/mol of either oxide}\]
The notion of looking at the enthalpy change as reflective of "stored energy" is important and suggestive. Observation indicates that chemically "stable" compounds tend to have very negative heats of formation. Carbon dioxide (-393.5 kJ/mol) and water (-285.5 kJ/mol) would be examples, but by no means the most extreme. Oxides of metals like iron(III) oxide and aluminum oxide have very negative heats of formation.
In contrast, chemically "unstable" compounds tend to have rather positive heats of formation. These very reactive substances have energy stored within their bonds. Silver fulminate, \(Ag_2C_2N_2O_2\), is a good example. The heat of formation is +180 kJ/mol.
Silver fulminate is one of a series of compounds containing transition metals and the "fulminate" group. All of the compounds are very unstable. When silver fulminate decomposes it does so according to the following reaction:
\[Ag_2C_2N_2O_2 \rightarrow 2 Ag + N_2 + 2 CO\]- The heat of formation for silver fulminate is +180 kJ/mol.
- The heat of formation for carbon monoxide is -110.5 kJ/mol.
How much energy is released in this reaction? If 0.0009 g of silver fulminate decomposes (as in the "Whipper Snappers" fireworks), how much energy is released?
Solution
\[ΔH_{rxn} = 2(-110.5 kJ) - 180 kJ = -401\; kJ/mol\]
So
\(0.0009\; g\) of silver fulminate is \(3 \times 10^{-6}\) moles.
\[(3 \times 10^{-6} mol) \times (401\; kJ/mol) = 0.001 \;kJ\]
Information like this seems to indicate that there might be a "preference" in Nature for reactions in which the enthalpy change is negative---loss of energy seems to breed chemical "stability". Substances which don't meet that criterion tend to react until they do. Or do they?

