Statistical Entropy - Mass, Energy, and Freedom
- Page ID
- 44608
The universe is made up of bits of matter, and the bits of matter have mass and energy. Neither mass nor energy may be created or destroyed, but in some special cases interconversions between mass and energy may occur. The things that happen in nature occur because matter is trying to gather to itself as much mass as it can (gravity) and to release as much of its energy as it can (the Sun, for example). This gathering of mass and loss of energy requires a price to be paid - the price of freedom. It seems that mass, energy, and freedom are the coins of the universe. Mass and energy must be conserved: if one part of the universe gathers more "wealth" as mass or energy, those must come from somewhere else in the universe, so there is always competition in the trading of these commodities. Freedom, on the other hand, is not conserved. However, there are some strange restraints on freedom. The freedom of the universe can take many forms, and appears to be able to increase without limit. However, the total freedom of the universe is not allowed to decrease.
The energy or the mass of a part of the universe may increase or decrease, but only if there is a corresponding decrease or increase somewhere else in the universe. The freedom in that part of the universe may increase with no change in the freedom of the rest of the universe. There might be decreases in freedom in the rest of the universe, but the sum of the increase and decrease must result in a net increase. There can be a decrease in the freedom in one part of the universe, but ONLY if there is an equal or greater increase in the rest of the universe.
There can be a decrease in the freedom in one part of the universe, but ONLY if there is an equal or greater increase in the rest of the universe
Most of us have a general idea of what mass and energy are, and we may have a fair understanding of how we can quantify them, or to say how much of them we have. Freedom is a more complicated concept. The freedom within a part of the universe may take two major forms: the freedom of the mass and the freedom of the energy. The amount of freedom is related to the number of different ways the mass or the energy in that part of the universe may be arranged while not gaining or losing any mass or energy. We will concentrate on a specific part of the universe, perhaps within a closed container. If the mass within the container is distributed into a lot of tiny little balls (atoms) flying blindly about, running into each other and anything else (like walls) that may be in their way, there is a huge number of different ways the atoms could be arranged at any one time. Each atom could at different times occupy any place within the container that was not already occupied by another atom, but on average the atoms will be uniformly distributed throughout the container. If we can mathematically estimate the number of different ways the atoms may be arranged, we can quantify the freedom of the mass. If somehow we increase the size of the container, each atom can move around in a greater amount of space, and the number of ways the mass may be arranged will increase.
Now let us turn to the freedom of the energy within the container. If the mass is in the form of atoms flying around, energy is only in the form of the kinetic energy of these atoms, and the energy of the electrons in the atoms moving around their nucleus (and sometimes we have to consider the neutrons, protons, and other stuff moving around in the nucleus). An atom's kinetic energy is related to its mass and its velocity. The energy in the container is the sum of the kinetic energies of all of the atoms, but the velocity is not the same for each atom, and the atoms are continually exchanging this energy through collisions with each other and through collisions with the walls. In the same way that the mass may have freedom in the number of ways the atoms may be arranged in space, the energy may have freedom in the number of ways that the velocities and directions of the atoms may be arranged. The velocities of the molecules are closely related to the temperature.
The energy and freedom of gaseous atoms appear only in velocities and directions, and is called translational energy and translational freedom. In the case of molecules (a molecule is a group of two or more atoms held together by chemical bonds) there are additional freedoms and additional forms of energy. Bonds between atoms act as springs allowing the atoms to vibrate within the molecule, so that the molecules may contain different levels of vibrational energy and vibrational freedom. Additionally, the entire molecule may rotate on different axes, allowing different levels of rotational energy and rotational freedom.
While the freedom of mass is related to the volume in which the mass is distributed, the freedom of energy is related to the temperature. An increase in the temperature of a gas leads directly to an increase in energy, and this can only occur if there is a decrease in energy somewhere else in the universe. We say that energy is transferred to the gas and the container (we will call that the "system")) from somewhere in the remainder of the universe (we will call that the "surroundings"). The increase in energy is accompanied by an increase in the energetic freedom of the system.
The thermodynamic term for quantifying freedom is entropy, and it is given the symbol \(S\). Like freedom, the entropy of a system increases with the temperature and with volume. The effect of volume is more easily seem in terms of concentration, especially in the case of mixtures. For a certain number of atoms or molecules, an increase in volume results in a decrease in concentration. Therefore, the entropy of a system increases as the concentrations of the components decrease. The part of entropy which is determined by energetic freedom is called thermal entropy, and the part that is determined by concentration is called configurational entropy.
The units of entropy are the same as those of heat capacity and of the gas law constant. The product of entropy (or a change in entropy) and the absolute temperature has the same units as energy (or a change in energy).
- The First Law of Thermodynamics states that the energy of the universe is constant.
- The Second Law of Thermodynamics states that the entropy of the universe cannot decrease.
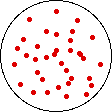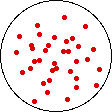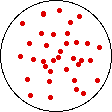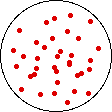
If the temperature of a gas is increased while the volume remains constant, the energy of the gas is increased and there is an increase in energetic freedom or thermal entropy. There is no change in concentration, and no change in configurational entropy.
| This process involves: Increase in Temperature, Increase in Energy, and Increase in Thermal Entropy | ||
 |
|
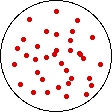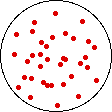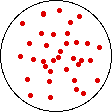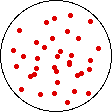 |
| Results: No Change in Volume or Concentration and No Change in Configurational Entropy | ||
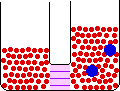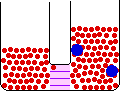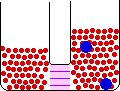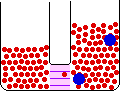
If the volume of the gas is increased while the temperature remains constant, the energy of the gas does not change and there is no change in thermal entropy. The increase in volume lowers the concentration and there is an increase in configurational entropy.
|
|
||
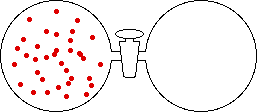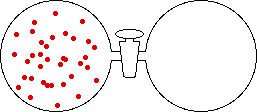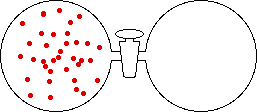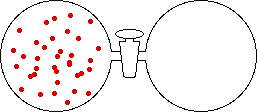 |
→ |
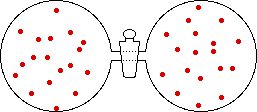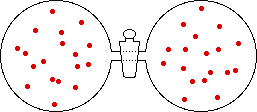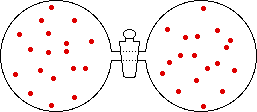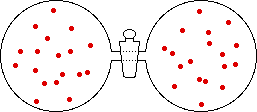 |
| Results: Increase in Volume, Decrease in Concentration, and Increase in Configurational Entropy | ||
The opening paragraph stated that matter tends to draw more matter to itself and tries to reduce its energy. There is also the tendency to increase its freedom and thus its entropy. There is a natural conflict between these tendencies to lower energy and increase entropy, since a reduction in energy is usually accompanied by a reduction in freedom and entropy. For changes in which the initial and final temperatures are the same, these are combined into a net tendency for a system to change, in which the symbol \(U\) is used for energy and \(T\) is the absolute temperature.
\[ΔU - TΔS \label{eq10}\]
in which \(ΔU\) and \(ΔS\) represent the changes in energy and entropy that would be measured for the change IF it occurred. If this net quantity is positive, the change cannot occur without some additional help. If this quantity is negative, the change might occur but there is no guarantee that it will occur. However, when the quantity is negative, the reverse change cannot occur without additional help. Changes that actually occur when this quantity is less than zero are said to be spontaneous or irreversible.
If the quantity in Equation \ref{eq10} is equal to zero, the change will not occur, but it could be pushed either forward or backward with very little additional help. This condition is described as equilibrium, and the change is said to be reversible.
Physical States
Crystal: A crystalline solid has very little movement and it is in a very low energy state. Movement of the atoms or molecules is limited to vibrations around a fixed point, so there is very little thermal entropy. The atoms/molecules are very close together (high concentration) and they are arranged in a very specific configuration (the crystal structure) which is repeated over and over within the crystal. There is very little freedom in the ways that the mass can be arranged, so the crystalline state has very little configurational entropy.

Liquid: When a solid melts, the atoms/molecules begin to move around, and perhaps also rotating and vibrating. The liquid has considerably more energy than the solid and thus has more thermal entropy. The volume does not change appreciably when a solid melts. Normally there is a small increase in volume on melting (the solid sinks in the liquid), but a few materials (water is one of them) show a decrease in volume on melting (the solid floats in the liquid). Normally there is a small increase in configurational entropy, but for materials like water there is a small decrease. Overall, there is an increase in both energy and entropy when a solid melts.

Gas: When a liquid vaporizes, the atoms/molecules receive a huge increase in energy - so large that it seems like they are no longer subject to gravity. There is a large increase in volume and the concentration becomes very small. There is a correspondingly large increase in freedom, so that both the thermal entropy and the configurational entropy are greatly increased.

Phase Transitions
Melting (fusion): Both energy and entropy increase on melting, so ΔU and ΔS are positive for fusion. At low temperatures (below the melting point) the positive ΔU contributes more than \(TΔS\) so the quantity
\[ΔU - TΔS\]
is positive, and melting cannot occur. As the temperature is raised however, both ΔU and ΔS increase but TΔS increases much more rapidly than ΔU. The quantity above will eventually become equal to zero at some temperature (the melting point) and the solid will spontaneously melt at any higher temperature. The opposite of melting is freezing.
Boiling (vaporization): Both \(ΔU\) and \(ΔS\) are large and positive for vaporization. The configurational entropy of the gas is related to the concentration of the gas molecules, so ΔS is greater for smaller concentrations of molecules in the vapor. This allows a balance between \(ΔU\) and \(TΔS\) at low temperatures, providing the concentration of gas molecules (and the vapor pressure) is sufficiently low. As the temperature is raised, this balance is maintained by an increase in the concentration of the gas molecules (and an increase in vapor pressure).
This results in a wide range of temperatures for a liquid and its vapor to be in equilibrium, with the vapor pressure increasing as the temperature is raised. The temperature at which the vapor pressure is exactly 1 atmosphere is defined as the normal boiling point of the liquid. The opposite of vaporization is condensation.
Sublimation: In the same way that \(ΔU\) and \(TΔS\) can balance for a liquid with its vapor at very low temperature, a similar balance can occur for a solid and its vapor below the melting point. For most solids, the vapor pressure is so low that we aren't concerned about it. However, we can see the effect in snow disappearing from a rooftop on a cold day without ever melting. This process is called sublimation. For a few solids (carbon dioxide or "dry ice" is one) the vapor pressure reaches 1 atmosphere at a temperature below the melting point, so that we never see the liquid at atmospheric pressure. The liquid state can be observed, however, at higher pressures and pressurized cylinders of carbon dioxide usually contain a mixture of the liquid and the gas. The opposite of sublimation is deposition.
Solutions
When pure materials in some physical state are mixed to form a solution in the same physical state at the same temperature and pressure, the process is called mixing. The energy change on mixing may be either positive or negative, but the entropy change is always positive. The entropy change is due mainly to the decrease in the concentrations of the individual components in the change from a limited volume in the pure state to a much larger volume in the mixed state.
 |
Small Change in Energy Small Change in Thermal Entropy --> Small Change in Volume Decrease in Concentration of Red Molecules Decrease in Concentration of Blue Molecules Increase in Configurational Entropy |
 |
When the mixed components are roughly equal in concentration, they are usually just called components (component A and component B, or components 1 & 2). For these solutions, concentrations are usually expressed in mole fractions, and occasionally in mass fractions or volume fractions.
When the concentration of one component in a liquid solution is much greater than the others, it is usually called the solvent, and the less-concentrated components are called solutes. For these solutions, the concentration of the solute may be expressed as mole fraction, molality (moles of solute per kilogram of solvent), or molarity (moles of solute per liter of solution). If needed, the concentration of solvent is usually expressed as mole fraction.
Solubility of Solutes
Before mixing, the pure solute may have been a gas, a liquid, or a solid. The first bit of solute that dissolves will have an extremely low concentration, so the change in configurational entropy for that dissolution will be very large if the pure solute is a liquid or a solid. If the pure solute is a gas, the change in configurational entropy will depend on the concentration of the gas. In all cases, the change in thermal entropy may be positive or negative, but the configurational entropy usually dominates at very low concentrations.
We can get a "feel" for the energy change as something dissolves. If the solution becomes colder as the solute dissolves, the energy change is positive since energy will have to be transferred to the solution in order to bring it back to the original temperature. If the solution becomes hotter as the solute dissolves, the energy change is negative since energy will have to be removed from the solution in order to return to the initial temperature.
If the energy change is positive and unfavorable the positive entropy change may allow a small amount of the solute to dissolve. However, as more of the solute dissolves the concentration increases and the entropy change decreases until the energy change is exactly balanced by \(TΔS\) and no more of the solute will dissolve. The concentration at this point determines the solubility of the solute in the solvent at this temperature. When there is a positive energy change for dissolution, an increase in temperature increases the effect of the positive entropy change and the solubility of the solute increases.
In the case of gases dissolving in liquids, the solubility of the gas depends on the concentration of the gas molecules. As the concentration in the gas phase increases, the concentration in the liquid phase increases. At low concentrations there is a direct proportionality between the concentrations in the two phases. This relationship is generally known as Henry's Law. Its most common form is for the concentration in the vapor phase to be represented by the partial pressure of the solute and for the concentration in the liquid phase to be represented by the mole fraction of the solute.
Henry's Law is normally associated with the solute in dilute solutions, but it also applies to the solvent in these dilute solutions. The application to the solvent is a special case of Henry's Law, called Raoult's Law. Raoult's Law states that the vapor pressure (or partial pressure) of the solvent becomes equal to the mole fraction of the solvent multiplied by the vapor pressure of the pure solvent when the solutes become very dilute.
Colligative Properties (Solvent)
Colligative properties of solutions are properties which depend only on the concentration of the solvent, and are independent of what the solute might be. Raoult's Law is the most basic example of a colligative property, because the vapor pressure (or partial pressure) of the solvent is determined only by the mole fraction of the solvent in a sufficiently dilute solution. This is usually stated as vapor pressure lowering by a non-volatile solute: The difference between the vapor pressure of the solution and that of the pure solvent is proportional to the mole fraction of solute.
All colligative properties are based on the fact that the concentration of the solvent is greatest when the solvent is pure, and the concentration of the solvent decreases as solute is added. When applied to freezing and melting, the entropy change is greater for the frozen pure solvent to melt when a solute is present than when the liquid phase is pure, and the solvent can melt at a lower temperature. This freezing point depression depends only on the concentration of the solvent and not on the nature of the solute, and is therefore a colligative property.
In a similar fashion, when a solution containing a solvent and a non-volatile solute is heated to near its boiling point at 1 atmosphere pressure, the entropy of the solvent in the solution is greater than in the pure liquid. This makes the entropy change for vaporization from the solution less than from the pure liquid, and the solvent will not boil until the temperature is higher than the normal boiling point. This boiling point elevation is also a colligative property.
In some cases, a solvent may be separated from a solution containing a solute by a semi-permeable membrane. The solvent can move through the pores in this membrane, but the solute is unable to move through the pores because of its size or perhaps its charge or polarity. This movement of the solvent is called osmosis. Since the concentration of the solvent is lower in the solution than in the pure liquid, the solvent molecules have greater entropy in the solution, and there is a tendency for the molecules to move through the membrane. As the solvent molecules move, the liquid level of the solution becomes higher than that of the pure liquid, and eventually the pressure becomes sufficient to prevent any more solvent molecules from crossing the membrane. This pressure difference between the solution and the pure solvent is called the osmotic pressure. Osmotic pressure is a colligative property.
This discussion has carefully avoided associating entropy with order and disorder. Instead, the focus has been on different types of freedom. Many textbooks use the order/disorder interpretation, and refer to examples such as the entropy of a shuffled deck of cards, or the entropy of a messy desk (or room) in comparison to a neat one. While these are strong images, the concept is basically incorrect.
The example with a deck of cards assumes that there is some order of the cards which represents perfect order. This simply happens to be the order given to a sealed deck by the manufacturer, namely each suit increasing from the Ace sequentially to the King, with alternating colors of the suits. That is no more orderly than starting with the 2 and increasing through the King to the Ace, or the reverse order. The deck could be arranged with all four Aces in some order of suits, followed by the four 2's in the same order of suits, etc. - that is also ordered. A new manufacturer may decide to package the decks in some order that has significance only to that manufacturer. Does that arrangement then become the perfect order for his product? Perhaps we should also be concerned with whether the cards are all facing the same direction.
The point is that there are many possible arrangements of the cards in a deck. When the cards are randomly and thoroughly shuffled, each of these arrangements has equal probability of occurring. When an arrangement is established, there is no freedom for the deck to acquire any other arrangement unless someone shuffles it or rearranges it in some manner. Since there is no freedom for that arrangement, there is no entropy associated with a single arrangement.
On the other hand, if a very large number of decks of cards are thoroughly and randomly shuffled, there are many possibilities for the arrangements of the cards within the different decks. When this idea of different arrangements of the cards is applied to atoms and molecules in solids and liquids, the number of possible arrangements create freedom of arrangement, a type of configurational entropy - not for any specific deck, but for the group of decks - or the ensemble (technically, the ensemble is the huge imaginary group of all of these decks arranged in all of the possible arrangements) of decks. The number of possible arrangements of the 52 cards in a deck is 52! (fifty-two factorial) which is equal to 52 x 51 x 50 x 49 x...x 3 x 2 x 1, an astronomical number. If these cards were atoms or molecules, the entropy due to this incredible amount of freedom would be related to the number of randomized decks multiplied by the natural logarithm of 52!. We can calculate the entropy per deck by dividing the entropy of the group of decks by the number of decks, but it is important to differentiate between the entropy per deck (which is a property of the group) and the entropy of a single deck (which really has no meaning in chemical systems).
Contributors and Attributions
Gary L Bertrand, Professor of Chemistry, University of Missouri-Rolla

