Enthalpy Change of Solution
- Page ID
- 3811
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page looks at the relationship between enthalpies of solution, hydration enthalpies and lattice enthalpies.
Enthalpy change of solution
The enthalpy change of solution is the enthalpy change when 1 mole of an ionic substance dissolves in water to give a solution of infinite dilution. Enthalpies of solution may be either positive or negative - in other words, some ionic substances dissolved endothermically (for example, NaCl); others dissolve exothermically (for example NaOH).
An infinitely dilute solution is one where there is a sufficiently large excess of water that adding any more does not cause any further heat to be absorbed or evolved. So, when 1 mole of sodium chloride crystals are dissolved in an excess of water, the enthalpy change of solution is found to be +3.9 kJ mol-1. The change is slightly endothermic, and so the temperature of the solution will be slightly lower than that of the original water.
Thinking about dissolving as an energy cycle
Why is heat sometimes evolved and sometimes absorbed when a substance dissolves in water? To answer that it is useful to think about the various enthalpy changes that are involved in the process. You can think of an imaginary process where the crystal lattice is first broken up into its separate gaseous ions, and then those ions have water molecules wrapped around them. That is how they exist in the final solution.
- The heat energy needed to break up 1 mole of the crystal lattice is the lattice dissociation enthalpy.
- The heat energy released when new bonds are made between the ions and water molecules is known as the hydration enthalpy of the ion. The hydration enthalpy is the enthalpy change when 1 mole of gaseous ions dissolve in sufficient water to give an infinitely dilute solution. Hydration enthalpies are always negative.
Factors affecting the size of hydration enthalpy
Hydration enthalpy is a measure of the energy released when attractions are set up between positive or negative ions and water molecules.
- With positive ions, there may only be loose attractions between the slightly negative oxygen atoms in the water molecules and the positive ions, or there may be formal dative covalent (co-ordinate covalent) bonds.
- With negative ions, hydrogen bonds are formed between lone pairs of electrons on the negative ions and the slightly positive hydrogens in water molecules.
The size of the hydration enthalpy is governed by the amount of attraction between the ions and the water molecules.
- The attractions are stronger the smaller the ion. For example, hydration enthalpies fall as you go down a group in the Periodic Table. The small lithium ion has by far the highest hydration enthalpy in Group 1, and the small fluoride ion has by far the highest hydration enthalpy in Group 7. In both groups, hydration enthalpy falls as the ions get bigger.
- The attractions are stronger the more highly charged the ion. For example, the hydration enthalpies of Group 2 ions (like Mg2+) are much higher than those of Group 1 ions (like Na+).
Estimating enthalpies of solution from lattice enthalpies and hydration enthalpies
The hydration enthalpies for calcium and chloride ions are given by the equations:
![]()

![]()
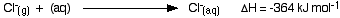
The following cycle is for calcium chloride, and includes a lattice dissociation enthalpy of +2258 kJ mol-1. We have to use double the hydration enthalpy of the chloride ion because we are hydrating 2 moles of chloride ions. Make sure you understand exactly how the cycle works.

So . . .
ΔHsol = +2258 - 1650 + 2(-364)
ΔHsol = -120 kJ mol-1
Whether an enthalpy of solution turns out to be negative or positive depends on the relative sizes of the lattice enthalpy and the hydration enthalpies. In this particular case, the negative hydration enthalpies more than made up for the positive lattice dissociation enthalpy.
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


