Set 4 – Nuclear Coupling
- Page ID
- 79418
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)I begin this part of the unit by presenting the students with the following question.
Consider the two hydrogen atoms HA and HB in the compound shown below. The X and Y groups are not hydrogen atoms and produce no magnetic fields. In particular, let’s focus on the effect that HB has on HA. We can think of HA “looking over” at HB and ask ourselves about the magnetic field produced by HB.
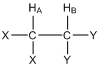
What do you know from earlier in this unit about the magnetic field produced by HB?
The students remember that the two possibilities are “with” and “against”. I also ask them about the distribution of the two states and they remember that it is essentially 50:50.
Is the flip of HB’s spin between the “with” and “against” states rapid or slow?
Most groups are able to reason this out by thinking about the relaxation time, but it may be necessary to prompt some groups to consider this. Once we’ve answered the question, I describe the difference between a case where the flipping is fast (time average of the magnetic field is zero), and the flipping is slow (either “with” or “against” the applied field).
This allows us to draw something similar to Figure 13 on the text. I also like to point out more specifically how the magnetic field of HB is actually transmitted to HA through the intervening electrons as shown in Figure 14 in the text and is not a through-space effect.
What does the resonance for HA look like in the NMR spectrum?
Many students may already know that it should look like a doublet based on prior experience with NMR through an organic course, but now they often understand at a deeper level why the two peaks are observed and why they have the same area.
Which peak in the doublet corresponds to BHB “with” and which corresponds to BHB “against”?
Students may need to go back to look up and remind themselves which end of the spectrum corresponds to the high and low energy gap and frequency, but groups are able to answer this question. I then describe the concept of a coupling constant.
Can you think of a way to decouple a hydrogen atom like HB?
This is often a difficult question for students. A good prompt is to remind them that if HB were to rapidly undergo transitions between the ground (with) and excited (against) states, the magnetic field experienced by HA would average out to zero. I then ask them if they can remember a previous discussion in the unit where this happened. Usually this is enough for some students to remember back to the idea of a saturated transition. This allows us to discuss how applying a high power RF at the frequency needed to excite HB would lead to a decoupling.
What would the HB resonance look like?
Groups have no problem realizing that this will be a doublet.
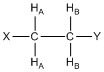
What would the resonance for HA look like in the compound shown below where there are two HB protons? Provide a rationale for your answer.

Before allowing students to answer this question, it is useful to remind them that there is rapid rotation about the C-C bond such that the two HB protons are chemically equivalent. They may already know from prior knowledge that it should be a triplet, and with the realization about being chemically equivalent, they can usually rationalize why a triplet is observed.
I also like to point out how the coupling constant of a triplet is calculated. I show them how this peak can also be thought of as a doublet of doublets similar to that shown in Figure 17 in the text to convince them how one measures the coupling constant of a triplet.
Which peak of the triplet corresponds to the WW and which to the AA situation?
Given the previous discussion of which peak was which in a doublet, groups quickly figure this out.
I then introduce the use of Pascal’s triangle (Figure 18 in the text) to show the number and intensity of peaks in the multiplets for coupled hydrogen atoms.
What factors do you think influence the magnitude of the coupling constant?
Groups are usually able to come up with distance as a factor. The idea that there is an angle term is something they don’t usually think of, especially since in prior experiences with NMR, they have usually examined systems with rapidly rotating bonds. They can be presented with a rigid bicyclic system as a way of thinking of something else that might be important in determining coupling constants or it may be appropriate to just tell them that there is an angular dependence to the coupling constant.
I then show them how the Newman projection can be used to define a dihedral angle, show them the two angular Karplus relationships for vicinal and geminal coupling, and ask them the following question.
Predict the coupling constants that would occur between HA, HM and HX and the mono-substituted alkene shown below and draw the shape of each resonance.
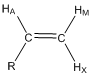
Using the two Karplus relationships, students are able to draw the resulting resonances. This is an excellent exercise to have different groups do at the board by drawing up the different resonances.
I then present them with the following example as a way of demonstrating why it is beneficial to have a higher field spectrometer.
Consider the following compound in which JAB = 10 Hz, \(\delta\)HA = 1.3 ppm and \(\delta\)HB = 1.2 ppm. Draw the resulting spectrum if the spectrum is recorded on a 100 MHz and 400 MHz spectrometer.
This is another problem that it may be good to have students work on at the board. I show them the two sets of X-axes with the chemical shift values identical for the two spectrometers, then encourage them to consider the Hertz in a ppm and draw the resonances. With this guidance, the groups are able to appreciate that the higher field instrument leads to better resolution of the two resonances.
I then describe how the situation is actually more complex than what is observed in their drawings and that coupled resonances with close chemical shifts exhibit a more complex behavior that complicates spectral interpretation. Figure 24 in the text is an example I show them to indicate how first-order rules of coupling break down when coupled resonances have close chemical shifts.


