EPR - Parallel Mode Operation
- Page ID
- 1796
This module presents the theory that describes how EPR transitions can be induced in integer high spin systems by the application of a modulating magnetic field parallel to the bond axis (z-axis), as well as some of the applications of this technique to various molecular systems.
Introduction
Standard mode Electron Paramagnetic Resonance (EPR), in which the modulating magnetic field is perpendicular to the applied field, is capable of detecting transitions between eigenstates in systems with fractional spins (i.e.; S=1/2, 3/2, ...), so called 'Kramer Systems'. This provides a sensitive experimental technique for detecting the electronic environment of unpaired electrons in various molecular systems. There are, however, systems with an integer spin value (ie; S=2), called 'Non-Kramer Systems'. In order to probe the electronic environment of such systems a method in which the modulating field is parallel to the applied field is employed. This method is called Parallel Mode EPR.
Spin Hamiltonian
To describe the theory of parallel mode EPR we must first define the system that we wish to characterize. If we have a ligand field that has axial symmetry, the collection of 2S+1 states of the system will be split, in the case of integral spin systems, into S doublets and a singlet. If we consider a system with S=2, the five states will be split into two doublets and a singlet. Application of a magnetic field gives the following spin Hamiltonian for the system.
\[\hat{H}=D[S_z^2-\frac{1}{3}S(S+1)]+E(S_x^2-S_y^2)+\beta\mathbf{B}\cdot\mathbf{g}\cdot\mathbf{S}\]
\[=D[S_z^2-\frac{1}{3}S(S+1)]+E(S_x^2-S_y^2)+g_{\parallel}\beta BS_z\cos{\theta}+g_{\perp}\beta BS_z\sin{\theta}\]
where the D is the axial field splitting term and E is the rhombic splitting term, these terms are a measure of the energy gap between the various states when no magnetic field is applied. These values are a reflection of the symmetry of the system. B is the magnetic field vector, \(\beta\) is the Bohr magneton, Sz is the z projection of the spin, and \(\theta\) is the angle of the applied magnetic field with respect to the symmetry axis of the system in the zx-plane.
Eigenfunctions and Eigenstates
If we have the condition that
\[ g\beta B\ll D \]
and we neglect the rhombic field splitting term in the spin Hamiltonian, then the states, and their respective energy values, are given by the following, to first order in perturbation theory.
\[\mid \pm2\rangle\Rightarrow E_{\pm2}=2D\pm 2g_{\parallel}\beta B\cos{\theta}\]
\[\mid \pm1\rangle\Rightarrow E_{\pm1}=-D\pm g_{\parallel}\beta B\cos{\theta}\]
\[\mid 0\rangle \rightarrow E_0=-2D\]
Analysis of the energy matrix of these states shows that there are no non-zero elements for the terms that represent transitions in the doublet states. Therefore these states have no allowed transitions. We will employ a mathematical trick to describe these states in a way that allows us to ascertain the EPR transitions that are allowed for the given system. We will adopt a new set of basis functions
which are symmetric and antisymmetric linear combinations, respectively, of the form
\[\mid2^s\rangle=\dfrac{1}{\sqrt{2}}(\mid+2\rangle+\mid-2\rangle)\]
\[\mid2^a\rangle=\dfrac{1}{\sqrt{2}}(\mid+2\rangle-\mid-2\rangle)\]
Since these basis functions are linear combinations of basis functions that are eigenfunctions of the spin Hamiltonian, it follows that these linear combinations are also eigenfunctions of the spin Hamiltonian. When this change of basis is adopted, and we account for the rhombic field splitting term in the spin Hamiltonian we obtain the following energies, correct to second order in perturbation theory.
\[E_{\pm2}=2D+\dfrac{(g_{\perp}\beta B\sin{\theta})^2}{E_2-E_1}+\frac{1}{2}\Delta_2\pm[(2g_{\parallel}\beta B\cos{\theta})^2+\left(\dfrac{\Delta_2}{2}\right)^2]^{1/2}\]
\[E_{\pm1}=-D+\dfrac{(g_{\perp}\beta B\sin{\theta})^2}{E_1-E_2}+\dfrac{3(g_{\perp}\beta B\sin{\theta})^2}{2(E_1-E_0)}\pm\left[(g_{\parallel}\beta B \cos{\theta})^2+\left(3E+\dfrac{3(g_{\perp}\beta B\sin{\theta})^2}{2(E_1-E_0)}\right)^2\right]^{1/2}\]
\[E_0=-2D+\dfrac{12E^2}{E_0-E_2}+\dfrac{3(g_{\perp}\beta B\sin{\theta})^2}{E_0-E_1}\]
If we have no rhombic splitting term (E=0), there are no transitions in the \(\mid\pm2\rangle\) doublet that are allowed. However, for the \(\mid\pm1\rangle\) doublet, the states are actually a linear combination of the \(\mid1\rangle\), \(\mid0\rangle\), and \(\mid-1\rangle\) states and, due to this admixture, for some value of \(\theta\) there is a weakly allowed transition. This is due to the second order Zeeman effects. This transition becomes forbidden in the case where \(\theta=0\), ie; when the magnetic field is oriented along the z-axis.
If E is not equal to zero then the \(\mid\pm2\rangle\) states are also linear combinations. If \(\theta=0\), we have energy levels for the \(\mid\pm2\rangle\) states that are given by the following
\[E_{\pm2}=\pm\dfrac{1}{2}[(4g_{\parallel}\beta B\cos{\theta})^2+\Delta_2^2]^{1/2}\]
where \(\Delta_2=\dfrac{12E^2}{E_2-E_o}\). The states of this doublet can then be written in the form
\[\mid+2^{\prime}\rangle=\cos{\alpha\mid+\rangle}+\sin{\alpha\mid-\rangle}\]
\[\mid-2^{\prime}\rangle=\cos{\alpha\mid+\rangle}-\sin{\alpha\mid-\rangle}\]
These new states, along with their respective energies and transitions, are shown schematically in Figure (1).
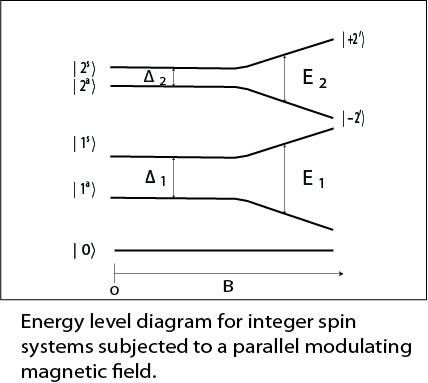
Transitions and the Resonance Condition
The states of the doublet described above have a matrix element that couples them together that is given by
\[\langle2+^{\prime}\mid 4g_{\parallel}\beta S_z\mid-^{\prime}\rangle=2g_{\parallel}\beta\sin{2\alpha}\]
This shows that there are allowed transitions in the \(\mid\pm2\rangle\) manifold as long as the modulating magnetic field is oriented with the z axis. The resonance condition for these transitions becomes
\[\Delta E=h\nu=[(4g_{\parallel}\beta B\cos{\theta})^2+\Delta^2]^{1/2}\]
and the probability of a transition occurring is given by
\[\mid\mu_z\mid^2=4g_{\parallel}^2\beta^2\dfrac{\Delta^2}{(h\nu)^2}\]
We have shown that, by taking linear combinations of the \(\mid\pm1\rangle\) and \(\mid\pm2\rangle\) states that show no transitions, we can construct a description of the system that accounts for the transitions observed in the parallel mode EPR spectra of integer spin systems.
Applications
The parallel mode electron paramagnetic resonance technique, in which the modulating magnetic field is parallel to the applied field, allows for the detection of transitions between eigenstates for systems with integer spin. This technique has been applied to a variety of systems to ascertain the nature of the spin states, some of which are described below.
Biophysical Applications
Both heme and non-heme iron proteins have been shown to posses high spin ferrous ions. The parallel mode EPR technique has been applied to several of these systems to verify their integer spin state. These proteins include the mononuclear ferrous sites of myoglobin and transferrin, as well as the polynuclear ferrous sites of methane monoxygenase, ferredoxin II, and aconitase. It has also been used to study the nature of the Mn(III)-Salen system and it's catalysis of the epoxidation of cis-beta-methylstyrene.
Inorganic Applications
Advances have been made in the field of synthetic inorganic chemistry such that there are now examples in the literature of synthetic high spin non-heme iron(IV) systems. This systems are predicted to have a high degree of reactivity and are being probed for their catalytic properties. The parallel mode EPR technique has been applied to these systems to extract the true nature of their spin state and to measure the g values of their absorptions. An example of a parallel mode EPR spectrum of a high spin (S=2) Fe(IV)-oxo compound, measured by Hendrich and coworkers at Pennsylvania State University, is shown in figure 2.
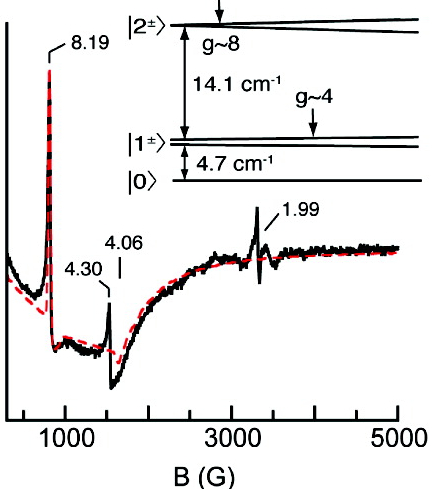
Parallel mode EPR has also been used to describe the spin state of other high spin inorganic complexes, including an S=6 chromium system synthesized by Piligko and coworkers at the University of Manchester.
Outside Links
- CalEPR facility website, www.brittepr.ucdavis.edu.
References
- Abragam, A. and Bleaney, B.; Electron Paramagnetic Resonance of Transition Ions; Dover Publishing; 1986.
- Weil, J. A. & Bolton, J. R. (2007). Electron Paramagnetic Resonance Spectroscopy: Elementary Theory and Applications, Second Edition. Wiley-Interscience.
- Hendrich, M. et al.; Biophysical Journal; (1989), 56, 489-500.
- Campbell, et al.; J. Am. Chem. Soc.; 2001; 123; 5710-5719.
- Piligko, et al.; Physical Review B; 2004; 69; 134424.
- Hendrich, M. et al.; J.A.C.S.; 2010; 132, 1-3.

