Using UV-visible Absorption Spectroscopy
- Page ID
- 3748
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page takes a brief look at how UV-visible absorption spectra can be used to help identify compounds and to measure the concentrations of colored solutions. It assumes that you know how these spectra arise, and know what is meant by terms such as absorbance, molar absorptivity and lambda-max. You also need to be familiar with the Beer-Lambert Law.
Using UV-absorption spectra to help identify organic compounds
If you have worked through the rest of this section, you will know that the wavelength of maximum absorption (lambda-max) depends on the presence of particular chromophores (light-absorbing groups) in a molecule.
For example, on another page you will have come across the fact that a simple carbon-carbon double bond (for example in ethene) has a maximum absorption at 171 nm. The two conjugated double bonds in buta-1,3-diene have a maximum absorption at a longer wavelength of 217 nm. We also talked about the two peaks in the spectrum of ethanal (containing a simple carbon-oxygen double bond) at 180 and 290 nm.
In carefully chosen simple cases (which is all you will get at this level), if you compared the peaks on a given UV-visible absorption spectrum with a list of known peaks, it would be fairly easy to pick out some structural features of an unknown molecule.
Lists of known peaks often include molar absorptivity values as well. That might help you to be even more sure. For example (again using the simple carbon-oxygen double bond), data shows that the peak at 290 nm has a molar absorptivity of only 15, compared with the one at 180 nm of 10000. If your spectrum showed a very large peak at 180 nm, and an extremely small one at 290 nm, that just adds to your certainty.
Using UV-absorption spectra to find concentrations
You should remember the Beer-Lambert Law:
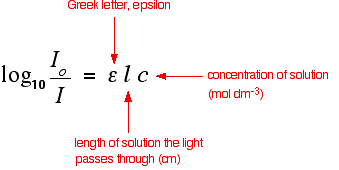
The expression on the left of the equation is known as the absorbance of the solution and is measured by a spectrometer. The equation is sometimes written in terms of that absorbance.
\[A = \epsilon \, l \, c\]
The symbol epsilon is the molar absorptivity of the solution.
Finding concentration using the molar absorptivity
If you know the molar absorptivity of a solution at a particular wavelength, and you measure the absorbance of the solution at that wavelength, it is easy to calculate the concentration. The only other variable in the expression above is the length of the solution. That's easy to measure and, in fact, the cell containing the solution may well have been manufactured with a known length of 1 cm.
For example, let's suppose you have a solution in a cell of length 1 cm. You measure the absorbance of the solution at a particular wavelength using a spectrometer. The value is 1.92. You find a value for molar absorptivity in a table of 19400 for that wavelength. Substituting those values:
\[ A = \epsilon l c\]
\[1.92 = 19400 \times 1 \times c\]
\[c=\dfrac{1.92}{19400}\]
\[= 9.90 \times 10^{-5}\; mol/l\]
Notice what a very low concentration can be measured provided you are working with a substance with a very high molar absorptivity. This method, of course, depends on you having access to an accurate value of molar absorptivity. It also assumes that the Beer-Lambert Law works over the whole concentration range (not true!). It is much better to measure the concentration by plotting a calibration curve.
Finding concentration by plotting a calibration curve
Doing it this way you don't have to rely on a value of molar absorptivity, the reliability of the Beer-Lambert Law, or even know the dimensions of the cell containing the solution.
What you do is make up a number of solutions of the compound you are investigating - each of accurately known concentration. Those concentrations should bracket the concentration you are trying to find - some less concentrated; some more concentrated. With colored solutions, this isn't a problem. You would just make up some solutions which are a bit lighter and some a bit darker in color.
For each solution, you measure the absorbance at the wavelength of strongest absorption - using the same container for each one. Then you plot a graph of that absorbance against concentration. This is a calibration curve.
According to the Beer-Lambert Law, absorbance is proportional to concentration, and so you would expect a straight line. That is true as long as the solutions are dilute, but the Law breaks down for solutions of higher concentration, and so you might get a curve under these circumstances. As long as you are working from values either side of the one you are trying to find, that isn't a problem.
Having drawn a best fit line, the calibration curve will probably look something like the next diagram. (I've drawn it as a straight line because it is easier for me to draw than a curve(!), and it's what you will probably get if you are working with really dilute solutions. But if it turns out to be a curve, so be it!)
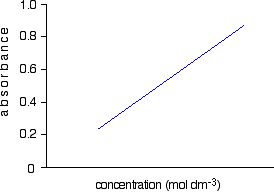
Notice that no attempt has been made to force the line back through the origin. If the Beer-Lambert Law worked perfectly, it would pass through the origin, but you can't guarantee that it is working properly at the concentrations you are using.
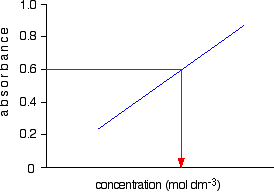
Now all you have to do is to measure the absorbance of the solution with the unknown concentration at the same wavelength. If, for example, it had an absorbance of 0.600, you can just read the corresponding concentration from the graph as above.
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


