7.39: Analysis of a Two-photon Quantum Eraser
- Page ID
- 142568
Greenberger, Horne and Zeilinger (GHZ) surveyed the then relatively new field of multiparticle interferometry in an August 1993 Physics Today article, ʺMultiparticle Interferometry and the Superposition Principle.ʺ This tutorial will use Mathcad and tensor algebra to analyze the results associated with Figure 5, which dealt with a two‐photon quantum eraser. A parametric down converter (PDC) produces two horizontally polarized, entangled photons, one taking the upper path and the other the lower path. The beams are combined at a beam splitter as shown below. Polarizing films oriented at angles of θ and ϕ relative to the horizontal are placed in front of detectors.
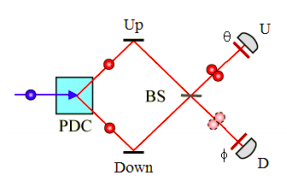
As the figure shows both photons, as bosons, arrive at either the U detector or the D detector. This result will now be confirmed using tensor algebra.
The photons emerging from the PDC are entangled and can be moving up or down and be in a particular polarization state. We use the following vectors to represent the motional and polarization states of the photons.
\[ u = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
\[ d = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
\[ \theta = \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \nonumber \]
\[ \phi = \begin{pmatrix} \cos \phi \\ \sin \phi \end{pmatrix} \nonumber \]
The motional and polarization photon states are combined using vector tensor multiplication. The up motional state is tagged with θ polarization, and the down state with ϕ polarization. The photon polarization states can be the same or different.
\[ u \theta = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} = \begin{pmatrix} \cos \theta \\ \sin \theta \\ 0 \\ 0 \end{pmatrix} \nonumber \]
\[ d \phi = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \begin{pmatrix} \cos \phi \\ \sin \phi \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \cos \phi \\ \sin \phi \end{pmatrix} \nonumber \]
There are four two‐photon output states at the detectors. These are also represented using tensor algebra. The first two letters refer to photon 1, the second two refer to photon 2. The uθdϕ (|uθ >1 |dϕ>2) state is constructed as an example.
\[ u \theta d \phi = \begin{pmatrix} \cos \theta \\ \sin \theta \\ 0 \\ 0 \end{pmatrix} \begin{pmatrix} 0 \\ 0 \\ \cos \phi \\ \sin \phi \end{pmatrix} \nonumber \]
\[ u \theta d \phi = ud( \theta, ~ \phi ) = \begin{pmatrix} 0 & 0 & \cos \theta \cos \phi & \cos \theta \sin \phi & 0 & 0 & \sin \theta \cos \phi & \sin \theta \sin \phi & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix} ^T \nonumber \]
The four output states are:
\[ uu ( \theta ) = \begin{pmatrix} \cos \theta ^2 & cos \theta \sin \theta & 0 & 0 & \sin \theta \cos \theta & \sin \theta ^2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix} ^T \nonumber \]
\[ ud ( \theta ,~ \phi ) = \begin{pmatrix} 0 & 0 & \cos \theta \cos \phi & \cos \theta \sin \phi & 0 & 0 & \sin \theta \cos \phi & \sin \theta \sin \phi & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix} ^T \nonumber \]
\[ du ( \phi, ~ \theta ) = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cos \phi \cos \theta & \cos \phi \sin \theta & 0 & 0 & \sin \phi \cos \theta & \sin \phi \cos \theta & \sin \phi \sin \theta & 0 & 0 \end{pmatrix} ^T \nonumber \]
\[ dd( \phi ) = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cos \phi ^2 & \cos \phi \sin \phi & 0 & 0 & \sin \phi \cos \phi & \sin \phi ^2 \end{pmatrix}^T \nonumber \]
The matrix operators required for this analysis are,
Identity:
\[ I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \nonumber \]
Mirror:
\[ M = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \nonumber \]
Beam splitter:
\[ BS = \begin{pmatrix} \frac{1}{ \sqrt{2}} & \frac{1}{ \sqrt{2}} \\ \frac{1}{ \sqrt{2}} & \frac{1}{ \sqrt{2}} \end{pmatrix} \nonumber \]
The mirrors and the beam splitter operate on the motional degree of freedom. Their operators as configured in the apparatus are constructed using matrix tensor multiplication, implemented with Mathcadʹs kronecker command.
\[ MI = \text{kronecker} (M,~ \text{kronecker} (I, ~ \text{kronecker} (M,~I))) \nonumber \]
\[ BSI = \text{kronecker} (BS,~ \text{kronecker} (I, ~ \text{kronecker} (BS,~I))) \nonumber \]
As mentioned earlier, the PDC produces the following entangled state of horizontally polarized photons:
\[ \Psi = \frac{1}{ \sqrt{2}} (ud(0,~0) + du(0,~0)) \nonumber \]
The output state after the photons interact with the mirrors and the beam splitter is:
\[ \Psi _{out} = BSI(MI) \Psi \nonumber \]
Initially the films in front of the detectors are horizontally polarized and we see that both photons always arrive at the same detector, as is shown graphically in the figure. Fifty percent of the time it is U and fifty percent of the time it is D. No U‐D coincidences are observed (off‐diagonal elements are zero).
\( \theta = 0\)
\( \phi = 0\)
\[ \begin{bmatrix} \left( \left| uu( \theta ) \Psi_{out} \right| \right)^2 & \left( \left| ud( \theta , \phi) \Psi_{out} \right| \right)^2 \\ \left( \left| du( \phi , \theta) \Psi_{out} \right| \right)^2 & \left( \left| dd( \phi ) \Psi_{out} \right| \right)^2 \end{bmatrix} = \begin{pmatrix} \frac{1}{2} & 0 \\ 0 & \frac{1}{2} \end{pmatrix} \nonumber \]
Now assume that a 90 degree polarization rotator is placed in the lower arm which rotates the horizontal state to the vertical polarization orientation. This provides path information and even though polarization is not measured in this experiment it has a significant affect on the measurement results.
The entangled state is now:
\[ \Psi = \frac{1}{ \sqrt{2}} \left( ud \left( 0,~ \frac{ \pi}{2} \right) + du \left( \frac{ \pi}{2} , ~ 0 \right) \right) \nonumber \]
\[ \Psi _{out} = BSI(MI) \Psi \nonumber \]
No photons are detected if the polarizers remain horizontally oriented or if they are both rotated to the vertical orientation.
\( \theta = 0\)
\( \phi = 0\)
\[ \begin{bmatrix} \left( \left| uu( \theta ) \Psi_{out} \right| \right)^2 & \left( \left| ud( \theta , \phi) \Psi_{out} \right| \right)^2 \\ \left( \left| du( \phi , \theta) \Psi_{out} \right| \right)^2 & \left( \left| dd( \phi ) \Psi_{out} \right| \right)^2 \end{bmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \nonumber \]
\( \theta = \frac{ \pi}{2}\)
\( \phi = { \pi}{2}\)
\[ \begin{bmatrix} \left( \left| uu( \theta ) \Psi_{out} \right| \right)^2 & \left( \left| ud( \theta , \phi) \Psi_{out} \right| \right)^2 \\ \left( \left| du( \phi , \theta) \Psi_{out} \right| \right)^2 & \left( \left| dd( \phi ) \Psi_{out} \right| \right)^2 \end{bmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \nonumber \]
However, if one of the polarizers is horizontal and the other vertical, U‐D coincidences are observed (non‐zero off‐diagonal elements).
\( \theta = 0\)
\( \phi = \frac{ \pi}{2}\)
\[ \begin{bmatrix} \left( \left| uu( \theta ) \Psi_{out} \right| \right)^2 & \left( \left| ud( \theta , \phi) \Psi_{out} \right| \right)^2 \\ \left( \left| du( \phi , \theta) \Psi_{out} \right| \right)^2 & \left( \left| dd( \phi ) \Psi_{out} \right| \right)^2 \end{bmatrix} = \begin{pmatrix} 0 & \frac{1}{8} \\ \frac{1}{8} & 0 \end{pmatrix} \nonumber \]
\( \theta = \frac{ \pi}{2}\)
\( \phi = 0\)
\[ \begin{bmatrix} \left( \left| uu( \theta ) \Psi_{out} \right| \right)^2 & \left( \left| ud( \theta , \phi) \Psi_{out} \right| \right)^2 \\ \left( \left| du( \phi , \theta) \Psi_{out} \right| \right)^2 & \left( \left| dd( \phi ) \Psi_{out} \right| \right)^2 \end{bmatrix} = \begin{pmatrix} 0 & \frac{1}{8} \\ \frac{1}{8} & 0 \end{pmatrix} \nonumber \]
The photon path information can be erased by a diagonal orientation of the polarizers. Now the coincidences of the previous cases disappears and the original bosonic behavior is restored.
\( \theta = \frac{ \pi}{4}\)
\( \phi = \frac{ \pi}{4}\)
\[ \begin{bmatrix} \left( \left| uu( \theta ) \Psi_{out} \right| \right)^2 & \left( \left| ud( \theta , \phi) \Psi_{out} \right| \right)^2 \\ \left( \left| du( \phi , \theta ) \Psi_{out} \right| \right)^2 & \left( \left| dd( \phi ) \Psi_{out} \right| \right)^2 \end{bmatrix} = \begin{pmatrix} \frac{1}{8} & 0 \\ 0 & \frac{1}{8} \end{pmatrix} \nonumber \]

