7.35: Bosonic and Fermionic Photon Behavior at Beam Splitters
- Page ID
- 142563
Photons from separate sources, u and d, arrive simultaneously at the beam splitter shown in the figure below.
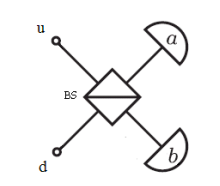
Because these photons are indistinguishable they do not possess separate identities, and we are forced by quantum mechanical principles to represent their collective state at the beam splitter (BS) by the following entangled wave function. The plus sign in this superposition indicates that photons are bosons; their wave functions are symmetric with respect to the interchange of the photon labels.
\[ \Psi = \frac{1}{ \sqrt{2}} (u_1 d_2 + d_1 u_2) \nonumber \]
Transmission and reflection occur at the 50‐50 beam splitters. By convention, reflection is assigned a π/2 phase shift relative to transmission. Thus, in the basis of the detectors, a and b, the photons originating in ports u and d evolve as follows.
\[ u = \frac{1}{ \sqrt{2}} (ia + b) \nonumber \]
\[ d = \frac{1}{ \sqrt{2}} (a + ib) \nonumber \]
Adding photon labels we have:
\[ u_1 = \frac{1}{ \sqrt{2}} (ia_1 + b_1) \nonumber \]
\[ u_2 = \frac{1}{ \sqrt{2}} (ia_2 + b_2) \nonumber \]
\[ d_1 = \frac{1}{ \sqrt{2}} (ia_1 + b_1) \nonumber \]
\[ d_2 = \frac{1}{ \sqrt{2}} (ia_2 + b_2) \nonumber \]
Substitution of these states into Ψ yields,
\[ \Psi = \frac{1}{ \sqrt{2}} (u_1 d_2 + d_1 u_2) ~ \begin{array}{|l}
\text{substitute},~ u_1 = \frac{1}{ \sqrt{2}} (i a_1 + b_1) \\
\text{substitute},~ u_2 = \frac{1}{ \sqrt{2}} (i a_2 + b_2) \\
\text{substitute},~ d_1 = \frac{1}{ \sqrt{2}} (a_1 + i b_1) \\
\text{substitute},~ d_2 = \frac{1}{ \sqrt{2}} (a_2 + i b_2) \\
\text{simplify} \\
\end{array} \rightarrow \Psi = \sqrt{2} \left( \frac{a_1 a_2}{2} + \frac{b_1 b_2}{2} \right) i \nonumber \]
Not surprisingly we see bosonic behavior by the photons. They both arrive at the same detector ‐ 50% of the time at detector a and 50% of the time at detector b.
However, recombining the photon beams at a second beam splitter before the detectors (see figure below) appears to invest them with fermionic character.
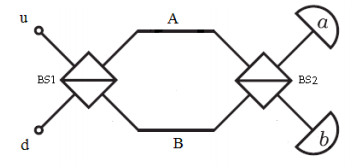
As was the case above, the entangled two-photon state at BS1 is,
\[ \Psi = \frac{1}{ \sqrt{2}} (u1 d2 +d1 u2) \nonumber \]
In terms of the BS1 output arms A and B, the photons originating in ports u and d evolve as,
\[ u = \frac{1}{ \sqrt{2}} (iA + B) \nonumber \]
\[ d = \frac{1}{ \sqrt{2}} (A + iB) \nonumber \]
While in terms of the detectors a and b, A and B in the presence of BS2 evolve as:
\[ A = \frac{1}{ \sqrt{2}} (ia + b) \nonumber \]
\[ B = \frac{1}{ \sqrt{2}} (a + ib) \nonumber \]
Thus, overall in the basis of the detectors, u and d evolve as follows.
\[ u = \frac{1}{ \sqrt{2}} \left[ i \left[ \frac{1}{ \sqrt{2}} (ia + b) \right] + \frac{1}{ \sqrt{2}} (a + ib) \right] = ib \nonumber \]
\[ d = \frac{1}{ \sqrt{2}} \left[ \frac{1}{ \sqrt{2}} (ia + b) + \left[ \frac{1}{ \sqrt{2}} (a + ib) \right] \right] = ia \nonumber \]
Attaching photon labels to u and d and substituting into Ψ yields:
\[ \Psi = - \frac{1}{ \sqrt{2}} (a_1 b_2 + b_1 a_2 ) \nonumber \]
Now we see fermionic behavior for the photons. They always arrive at different detectors.
This result can also be achieved as follows:
\[ \Psi = \frac{i}{ \sqrt{2}} (A_1 A_2 + B_1 B_2) ~ \begin{array}{|l}
\text{substitute},~ A_1 = \frac{1}{ \sqrt{2}} (i a_1 + b_1) \\
\text{substitute},~ A_2 = \frac{1}{ \sqrt{2}} (i a_2 + b_2) \\
\text{substitute},~ B_1 = \frac{1}{ \sqrt{2}} (a_1 + i b_1) \\
\text{substitute},~ B_2 = \frac{1}{ \sqrt{2}} (a_2 + i b_2) \\
\text{simplify} \\
\end{array} \rightarrow \Psi = \frac{ \sqrt{2} a_1 b_2 + a_2 b_1}{2} \nonumber \]
The two examples can also be analyzed using matrix algebra. Below we have the vectors for photon direction of propagation, the initial two‐photon entangled state, and the matrix representing a beam splitter.
\[ u = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
\[ d = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
\[ \Psi = \frac{1}{ \sqrt{2}} \left[ \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \right] \nonumber \]
After the second beam splitter they propagate in opposite directions, behaving like fermions.
\[ \text{kronecker} (BS,~BS) \text{kronecker} (BS,~BS) \Psi = \begin{pmatrix} 0 \\ -0.707 \\ -0.707 \\ 0 \end{pmatrix} \nonumber \]
\[ \Psi = frac{-1}{ \sqrt{2}} \left[ \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \end{pmarix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \right] \nonumber \]

