7.30: Another Two Photon Interference Experiment
- Page ID
- 142299
In this experiment a down converter, DC, converts an incident photon into two lower energy photons. One photon takes an upper path traveling left or right, and the other photon takes one of the lower paths traveling in the opposite direction. The results of this experiment are that both photons are recorded at either the A detectors or B detectors. One photon is never observed at an A detector while the other is observed at a B detector. A quantum mechanical analysis of this phenomena is provided below.
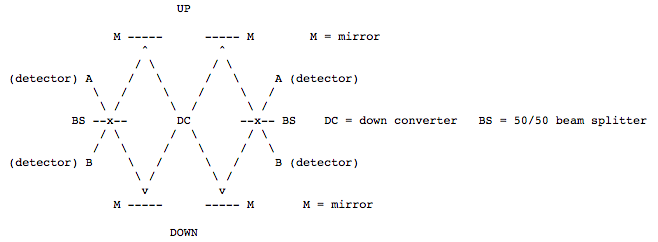
After the down converter the initial photon has evolved into a state which is an entangled linear superposition.
\[ |DC \rangle \frac{[ |up \rangle_1 |down \rangle_2 + |down \rangle_1 |up \rangle_2]}{2^{ \frac{1}{2}}} \nonumber \]
This is an entangled state (non-factorable) because it acknowledges that it is unknown which photon takes which path. It also incorporates the fact that photons are bosons and consequently the state function must be symmetric with respect to interchange of the coordinates (paths) of the photons. If photons were fermions, |DC> would have to be antisymmetric with respect interchange of coordinates and the positive sign in equation (1) would be replaced with a negative sign.
A photon that takes one of the upper paths has a 50% chance of being recorded at an A or a B detector. To reach A it must be reflected at the beam splitter and to reach B is must be transmitted. Conservation of energy requires a 90 degree phase difference between transmission and reflection, and by convention this phase difference is assigned to reflection. To reach detector A the upper photon must undergo a reflection at the beam splitter and its phase shift is recorded by multiplying |A> by i [(-1)1/2]. Thus in terms of the detector states |A> and |B> a photon taking an upper path evolves into the state shown in equation (2).
\[ |up \rangle \frac{[ i|A \rangle + |B \rangle ]}{2^{ \frac{1}{2}}} \nonumber \]
Similar arguments show that a photon taking one of the lower paths will evolve into the state given by equation (3).
\[ |down \rangle \frac{[ |A \rangle + i|B \rangle ]}{2^{ \frac{1}{2}}} \nonumber \]
When equations (2) and (3) are substituted into equation (1) the following final state results:
\[ |Source \rangle \frac{[ i|A \rangle_1 |A \rangle_2 + i^2 |A \rangle_1 |B \rangle_2 + |B \rangle_1 |A \rangle_2 + i |B \rangle_1 |B \rangle_2 + i|A \rangle_1 |A \rangle_2 + |A \rangle_1 |B \rangle_2 + i^2 |B \rangle_1 |A \rangle_2 + i |B \rangle_1 |B \rangle_2]}{2^{ \frac{3}{2}}} \nonumber \]
Thus there are eight final probability amplitudes, and they come in four pairs as can be seen above. However, two of the pairs destructively interfer (see note below) with each other and the final state is,
\[ |Source \rangle \frac{[ i|A \rangle_1 |A \rangle_2 + i |B \rangle_1 |B \rangle_2 ]}{2^{ \frac{1}{2}}} \nonumber \]
The probability of an outcome is found by taking the square of the absolute magnitude of its probability amplitude. Thus the probability that both photons will be observed at A detectors, or both photons will be observed at B detectors is calculated as follows:
\[ P(AA) = \left| \frac{1}{2} ^{ \frac{1}{2}} \right| ^2 = \frac{1}{2} \nonumber \]
\[ P(BB) = \left| \frac{i}{2} ^{ \frac{1}{2}} \right| ^2 = \frac{1}{2} \nonumber \]
It was noted earlier that fermions require anti-symmetric state functions. So if this experiment could be performed with fermions the results would be P(AA) = P(BB) = 0, and P(AB) = P(BA) = 1/2.
Note: "The things that interfere in quantum mechanics are not particles. They are probability amplitudes for certain events. It is the fact that probability amplitudes add up like complex numbers that is responsible for all quantum mechanical interferences." Roy J. Glauber, American Journal of Physics, 63(1), 12 (1995).
Reference: Greenberger, D. M.; Horne, M. A.; Zeilinger, A. Physics Today, 1993, 44(8), 22.

