7.23: The Ramsey Atomic Interferometer
- Page ID
- 141692
The Ramsey interferometer, which closely resembles the Mach-Zehnder interferometer, is constructed using two π/2 Rabi pulses (R1 and R2) separated by a phase shifter in the lower arm, as shown below.
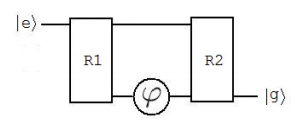
where
\[ |e \rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
\[ |g \rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
The matrix representations of the phase shifter and the Rabi elements are as follows:
\[ PhaseShift ( \phi) = \begin{pmatrix} 1 & 0 \\ 0 & e^{i \phi} \end{pmatrix} \nonumber \]
\[ Rabi( \phi) = \begin{pmatrix} \cos \left( \frac{ \theta}{2} \right) & - \sin \left( \frac{ \theta}{2} \right) \\ \sin \left( \frac{ \theta}{2} \right) & \cos \left( \frac{ \theta}{2} \right) \end{pmatrix} \nonumber \]
\[ Rabi \left( \frac{ \pi}{2} \right) = \begin{pmatrix} 0.707 & -0.707 \\ 0.707 & 0.707 \end{pmatrix} \nonumber \]
The input to the interferometer is the upper state |e> of a two-state atom. The first pulse behaves like a Hadamard gate creating a coherent superposition of |e> and the lower state of the atom, |g>.
\[ Rabi \left( \frac{ \pi}{2} \right) \begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} \frac{1}{2} 2^{ \frac{1}{2}} \\ \frac{1}{2} 2^{ \frac{1}{2}} \end{pmatrix} \nonumber \]
\[ \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} \nonumber \]
The phase shifter alters the superposition by adding a phase to |g>.
\[ PhaseShift( \phi ) Rabi \left( \frac{ \pi}{2} \right) \begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} \frac{1}{2} 2^{ \frac{1}{2}} \\ \frac{1}{2} e^{i \phi} 2^{ \frac{1}{2}} \end{pmatrix} \nonumber \]
\[ \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ e^{i \phi} \end{pmatrix} \nonumber \]
In the absence of a phase shift (ϕ = 0) the two π/2 pulses behave like a not gate yielding |g> at the output channel.
\[ Rabi \left( \frac{ \pi}{2} \right) PhaseShift(0) Rabi \left( \frac{ \pi}{2} \right) \begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
However if ϕ = π, the interferometer is equivalent to the identity operator and the output is |e>.
\[ Rabi \left( \frac{ \pi}{2} \right) PhaseShift( \pi) Rabi \left( \frac{ \pi}{2} \right) \begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
In general, the result is a superposition of |e> and |g>.
\[ Rabi \left( \frac{ \pi}{2} \right) PhaseShift ( \phi) Rabi \frac{ \phi}{2} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} \frac{1}{2} - \frac{1}{2} e^{i \phi} \\ \frac{1}{2} +\frac{1}{2} e^{i \phi} \end{pmatrix} \nonumber \]
\[ \begin{pmatrix} e \\ g \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 1 - e^{i \phi} \\ 1 + e^{i \phi} \end{pmatrix} \nonumber \]
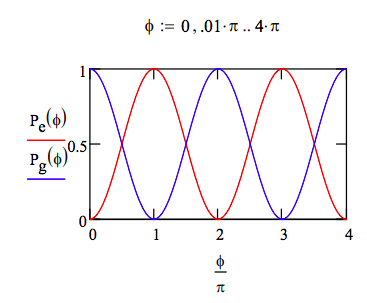
The probabilities of detecting |e> and |g> at the output channel depend on the phase ϕ, exhibiting interference effects as in the Mach-Zehnder interferometer with a phase shifter in the lower arm. This is shown below both algebraically and graphically.
\[ P_e ( \phi) = \left[ \left| \begin{pmatrix} 1 \\ 0 \end{pmatrix}^T Rabi \left( \frac{ \pi}{2} \right) PhaseShift ( \phi) Rabi \left( \frac{ \pi}{2} \right) \begin{pmatrix} 1 \\ 0 \end{pmatrix} \right| \right]^2 ~ simplify \rightarrow \frac{1}{2} - \frac{1}{2} \cos \phi \nonumber \]
\[ P_g ( \phi) = \left[ \left| \begin{pmatrix} 0 \\ 1 \end{pmatrix}^T Rabi \left( \frac{ \pi}{2} \right) PhaseShift ( \phi) Rabi \left( \frac{ \pi}{2} \right) \begin{pmatrix} 1 \\ 0 \end{pmatrix} \right| \right]^2 ~ simplify \rightarrow \frac{1}{2} + \frac{1}{2} \cos \phi \nonumber \]