7.14: Matrix Mechanics Approach to Polarized Light
- Page ID
- 140338
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
It is convenient to use matrix mechanics to describe experiments with polarized light. In this tutorial we will restrict our attention to plane polarized light. However, it would be just as easy to use matrix mechanics to describe the behavior of circularly polarized light.
The Three Polarizer Paradox
If two polarizing films are aligned in the same direction light from the first polarizer passes through the second. If the polarizers are opposed at a 90o angle, the polarized light transmitted from the first polarizer is absorbed by the second. If a third polarizer is sandwiched between the two opposed polarizers at a 45o angle some light gets through the last polarizer. This is illustrated below using Dirac notation for both the photons and the polarizers.
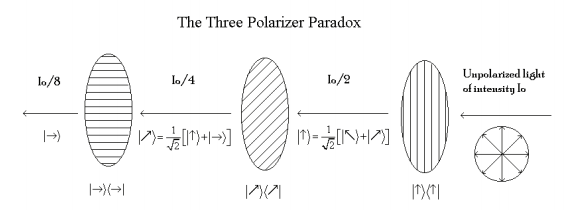
In what follows this demonstration is analyzed using the principles of matrix mechanics. Light polarized in the vertical and horizontal directions, and at an angle θ relative to the vertical can be represented by the following vectors,
\[ | v \rangle = \begin{pmatrix}
1 \\
0
\end{pmatrix} ~~~ |h \rangle = \begin{pmatrix}
0 \\
1
\end{pmatrix} | \Theta \rangle = \begin{pmatrix}
\cos \theta \\
\sin \theta
\end{pmatrix} \nonumber \]
The graphical representation between \( |v \rangle\), \(|h \rangle\) and \( | \theta \rangle\) is shown below.
As can be seen in this figure, | v ⟩ and | h ⟩ represent an orthonormal basis set, and | θ ⟩ represents a general vector in the space defined by | v ⟩ and | h ⟩. As is shown below it is a normalized state vector.
\[ \begin{pmatrix}
\cos \theta & \sin \theta
\end{pmatrix} \begin{pmatrix}
\cos \theta \\
\sin \theta
\end{pmatrix} = \cos^2 \theta + \sin^2 \theta = 1 \nonumber \]
Naturally | θ ⟩ can be written as a linear superposition of the polarization base states:
\[ | \Theta \rangle = | v \rangle \langle v | \Theta \rangle + |h \rangle \langle h | \Theta \rangle = |v \rangle \cos \theta + |h \rangle \sin \theta \nonumber \]
A polarizing filter (film) oriented in the veritcal direction in this basis can be represented by the following matrix operator.
\[ \hat{V} = \begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} \nonumber \]
Note the results of the following measurements on the three previously defined polarization states using this measurement operator.
\[ \begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} \begin{pmatrix}
1 \\
0
\end{pmatrix} = \begin{pmatrix}
1 \\
0
\end{pmatrix} \nonumber \]
\[ \begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} \begin{pmatrix}
0 \\
1
\end{pmatrix} = \begin{pmatrix}
0 \\
0
\end{pmatrix} \nonumber \]
\[ \begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} \begin{pmatrix}
\cos \theta \\
\sin \theta
\end{pmatrix} = \begin{pmatrix}
\cos \theta \\
0
\end{pmatrix} \nonumber \]
Vertically polarized light passes the vertical polarizer, horizontally polarized light is absorbed (annihilated), and θ-polarized light, if it passes, becomes vertically polarized with reduced intensity. The probability that it will pass the vertical polarizer is cos2θ.
The operators associated with a horizontal filter and a filter oriented at an angle θ relative to the vertical are given below.
\[ \hat{H} = \begin{pmatrix}
0 & 0 \\
0 & 1
\end{pmatrix} \nonumber \]
\[ \hat{ \Theta} = \begin{pmatrix}
\cos ^2 \theta & \sin \theta \cos \theta \\
\sin \theta \cos \theta & \sin^2 \theta
\end{pmatrix} \nonumber \]
The operator associated with a filter oriented at an angle θ relative to the vertical is generated as shown below.
\[ \hat{ \theta} = | \theta \rangle \langle \theta | = \begin{pmatrix}
\cos \theta \\
\sin \theta
\end{pmatrix} \begin{pmatrix}
\cos \theta & \sin \theta
\end{pmatrix} = \begin{pmatrix}
\cos ^2 \theta & \cos \theta \sin \theta \\
\sin \theta \cos \theta & \sin^2 \theta
\end{pmatrix} \nonumber \]
We now have the mathematical apparatus in place to examine the three-polarizer paradox using the basic principles of matrix mechanics. Unpolarized light, such as that coming from an incandecent light bulb, might be considered to be a mixture of all polarization angles between 0 and π radians. Assuming this, the probability amplitude that a θ-polarized photon will pass a vertically oriented filter is,
\[ \begin{pmatrix}
1 & 0
\end{pmatrix} \begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} \begin{pmatrix}
\cos \theta \\
\sin \theta
\end{pmatrix} \nonumber \]
The probability is the square of the absolute magnitude of the probability amplitude. Thus the fraction of a beam of unpolarized photons that will pass a vertically oriented polarizer is 0.5. To achieve this result we must integrate over all possible polarization angles. The normalization constant for this calculation is 2/π.
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left| \begin{pmatrix}
1 & 0
\end{pmatrix} \begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} \begin{pmatrix}
\cos \theta \\
\sin \theta
\end{pmatrix}\right| ^2 d \theta = 0.5 \nonumber \]
As is well known, and easy to demonstrate, the probability that unpolarized light (or light of any polarization) will pass two crossed polarizing films (vertical followed by horizontal, for example) is zero.
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left| \begin{pmatrix}
0 & 1
\end{pmatrix} \begin{pmatrix}
0 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} \begin{pmatrix}
\cos \theta \\
\sin \theta
\end{pmatrix}\right| ^2 d \theta = 0 \nonumber \]
However, if a polarizing film oriented at a 45o angle is inserted between the crossed polarizers light gets through the final horizontal filter. The operator for a 45o polarizer is obtained as follows:
\[ \theta = \frac{ \pi}{4} \nonumber \]
\[ \hat{ \Theta} = \begin{pmatrix}
\cos^2 \theta & \sin \theta \cos \theta \\
\sin \theta \cos \theta & \sin^2 \theta
\end{pmatrix} = \begin{pmatrix}
\frac{1}{2} & \frac{1}{2}\\
\frac{1}{2} & \frac{1}{2}
\end{pmatrix} \nonumber \]
The following calculation shows that 12.5% of the unpolarized light illuminating the initial vertical polarizer is transmitted through this arrangement of polarizing films.
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left| \begin{pmatrix}
0 & 1
\end{pmatrix} \begin{pmatrix}
0 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
\frac{1}{2} & \frac{1}{2}\\
\frac{1}{2} & \frac{1}{2}
\end{pmatrix} \begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} \begin{pmatrix}
\cos \theta \\
\sin \theta
\end{pmatrix}\right| ^2 d \theta = 0.125 \nonumber \]
It is easy to see that if the positions of the diagonal and horizontal polarizers are interchanged no light would be transmitted because the first and second polarizers would be crossed. This illustrates that the horizontal and diagonal polarization measurements do not commute; the outcome is dependent on the order of the measurements.
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left| \begin{pmatrix}
0 & 1
\end{pmatrix} \begin{pmatrix}
\frac{1}{2} & \frac{1}{2}\\
\frac{1}{2} & \frac{1}{2}
\end{pmatrix} \begin{pmatrix}
0 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} \begin{pmatrix}
\cos \theta \\
\sin \theta
\end{pmatrix}\right| ^2 d \theta = 0 \nonumber \]

