7.13: The Three-Polarizer Paradox
- Page ID
- 140336
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
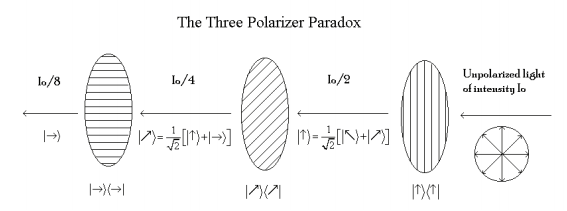
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A beam of unpolarized light illuminates a vertical polarizer and 50% of the light emerges vertically polarized. This light beam encounters a diagonal polarizer oriented at a 45 degree angle to the original vertical polarizer and 50% of it emerges as diagonally polarized light. Finally 50% of the diagonally polarized light passes a horizontally oriented polarizer. In other words 12.5% of the light illuminating the first vertical polarizer passes the final horizontal polarizer. However, if the diagonal polarizer sandwiched between the vertical and horizontal polarizers is removed, no light emerges form the final horizontal polarizer.
Using the figure below vector algebra will be used to analyze this so-called "three-polarizer paradox." The paradox being that it is surprising that the insertion of the diagonal polarizer between crossed polarizers allows photons to pass the final horizontal polarizer.
Eigenstate for a \( \Theta\)-polarized photon:
\[ \Theta ( \theta) = \begin{pmatrix}
\cos \theta
\sin \theta
\end{pmatrix} ~~~ \begin{pmatrix}
\cos \theta & \sin \theta
\end{pmatrix} \begin{pmatrix}
\cos \theta \\
\sin \theta
\end{pmatrix} simplify \rightarrow 1 \nonumber \]
Eigenstates for vertically, horizontally and diagonally polarized light (S (slant) represents D's orthogonal partner, just as V and H are orthogonal partners, or basis states):
\[ V = \Theta (0) \rightarrow \begin{pmatrix}
1 \\
0
\end{pmatrix} \nonumber \]
\[ H = \Theta (0) \left( \frac{ \pi}{2}\right) \rightarrow \begin{pmatrix}
0 \\
1
\end{pmatrix} \nonumber \]
\[ D = \Theta (0) \left( \frac{ \pi}{4}\right) float,~4~ \rightarrow \begin{pmatrix}
0.7071 \\
0.7071
\end{pmatrix} \nonumber \]
\[ S = \Theta (0) \left( - \frac{ \pi}{4}\right) float,~4~ \rightarrow \begin{pmatrix}
0.7071 \\
-0.7071
\end{pmatrix} \nonumber \]
Confirm with vector addition the superpositions shown in the figure:
\[ \frac{D + S}{ \sqrt{2}} = \begin{pmatrix}
1 \\
0
\end{pmatrix} \nonumber \]
\[ \frac{D - S}{ \sqrt{2}} = \begin{pmatrix}
0 \\
1
\end{pmatrix} \nonumber \]
\[ \frac{V + H}{ \sqrt{2}} = \begin{pmatrix}
0.707 \\
0.707
\end{pmatrix} \nonumber \]
\[ \frac{V - H}{ \sqrt{2}} = \begin{pmatrix}
0.707 \\
-0.707
\end{pmatrix} \nonumber \]
The polarizers are operators, and their matrices are the outer products of their polarization vectors:
\[ | \rightarrow \rangle \langle \rightarrow | ~~~ H H^T = \begin{pmatrix}
0 & 0 \\
0 & 1
\end{pmatrix} \nonumber \]
\[ | \nearrow \rangle \langle \nearrow | ~~~ D D^T = \begin{pmatrix}
0.5 & 0.5 \\
0.5 & 0.5
\end{pmatrix} \nonumber \]
\[ | \uparrow \rangle \langle \uparrow | ~~~ V V^T = \begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix} \nonumber \]
Unpolarized light is an even mixture of all polarization angles between 0 and \( \frac{ \pi}{2}\) radians. Probability is the absolute magnitude squared of the probability amplitude. The fraction of a beam of unpolarized light that will pass a vertically oriented polarizer is 0.5. To confirm this result we must integrate over all possible polarization angles, summing the squares of the probability amplitudes for each angle . The factor \( \frac{2}{ \pi}\) [( \(\pi\)/2)-1] normalizes the calculation.
Probability Amplitude:
\[ \langle V | \Theta \rangle ~~~ V^T \Theta ( \theta) \rightarrow \cos \theta \nonumber \]
Probability:
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} | \langle V | \Theta \rangle |^2 d \Theta \nonumber \]
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left( V^T \Theta ( \theta) \right)^2 d \theta = 0.5 \nonumber \]
As is well known, and easy to demonstrate, the probability that unpolarized light (or light of any polarization) will pass two crossed polarizing films (vertical followed by horizontal for example) is 0.
Probability Amplitude:
\[ \langle H | V \rangle \langle V | \Theta \rangle ~~~ H^T V V^T \Theta ( \theta) \rightarrow 0 \nonumber \]
Probability:
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} | \langle H | V \rangle \langle V | \Theta \rangle |^2 d \Theta \nonumber \]
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left( H^T V V^T \Theta ( \theta) \right)^2 d \theta = 0 \nonumber \]
However, if a polarizing film oriented diagonally at a 45 degree angle is inserted between the crossed polarizers light gets through the final horizontal filter. The following calculation shows that 12.5% of the unpolarized light illuminating the initial vertical filter gets through this arrangement of polarizing films in agreement with the figure above and experience.
Probability Amplitude:
\[ \langle H | V \rangle \langle D | V \rangle \langle V | \Theta \rangle ~~~ H^T D D^T V V^T \Theta ( \theta) ~ float,~1 \rightarrow 0.5 \cos \theta \nonumber \]
Probability:
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} | \langle H | V \rangle \langle D | V \rangle \langle V | \Theta \rangle |^2 d \Theta \nonumber \]
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left( \right| H^T D D^T V V^T \Theta ( \theta) \left| \right)^2 d \theta = 0.125 \nonumber \]
The three probabilities can be also calculated by an equivalent method that explicitly treats the polarizers as measurement operators. From above we see that, \(V_{op} = VV^T\), \( H_{op} = HH^T\), \( D_{op} = D D^T\), and write the probability calculations as follows.
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left( V^T V_{op} \Theta ( \theta) \right)^2 d \theta = 0.5 \nonumber \]
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left( H^T V_{op} \Theta ( \theta) \right)^2 d \theta = 0 \nonumber \]
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left( H^T D_{op} V_{op} \Theta ( \theta) \right)^2 d \theta = 0.125 \nonumber \]

