7.4: Single Photon Interference - Fourth Version
- Page ID
- 137794
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
This analysis of the operation of a Mach-Zehnder Interferometer (MZI) will use tensor algebra and the creation and annihilation operators.
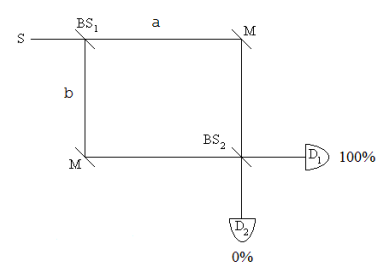
An interferometer arm can be occupied or unoccupied. These states are represented by the following vectors.
\[ Unoccupied: | 0 \rangle = \begin{pmatrix}
1 \\
0
\end{pmatrix} \nonumber \]
\[ Occupied: | 1 \rangle = \begin{pmatrix}
0 \\
1
\end{pmatrix} \nonumber \]
After the first beam splitter the photon is in an even superposition of being in both arms of the interferometer. By convention a 90 degree phase shift is assigned to arm b to preserve probability. In terms of the concept of occupation, the superposition takes the following form in tensor algebra.
\[ |S \rangle \xrightarrow{i} \frac{1}{ \sqrt{2}} [|1 \rangle_a | 0 \rangle_b + i | 0 \rangle_a 1 | \rangle_b ] = \frac{1}{ \sqrt{2}} \bigg[ \begin{pmatrix}
0\\
1
\end{pmatrix}_a \otimes \begin{pmatrix}
1\\
0
\end{pmatrix}_b + i \begin{pmatrix}
1\\
0
\end{pmatrix}_a \otimes \begin{pmatrix}
0\\
1
\end{pmatrix}_b \bigg] = \frac{1}{ \sqrt{2}} \begin{pmatrix}
0\\
i\\
1\\
0
\end{pmatrix} \nonumber \]
\[ \Psi = \frac{1}{ \sqrt{2}} \begin{pmatrix}
0\\
i\\
1\\
0
\end{pmatrix} \nonumber \]
The matrix operators required for this analysis are as follows.
Creation:
\[ C = \begin{pmatrix}
0 & 0 \\
1 & 0
\end{pmatrix} \nonumber \]
Annihilation:
\[ A = \begin{pmatrix}
0 & 0 \\
1 & 0
\end{pmatrix} \nonumber \]
Number:
\[ N = \begin{pmatrix}
0 & 0 \\
1 & 0
\end{pmatrix} \nonumber \]
Identity:
\[ I = \begin{pmatrix}
0 & 0 \\
1 & 0
\end{pmatrix} \nonumber \]
The effect of the creation, annihilation and number operators on |0> and |1>:
\[ C \begin{pmatrix}
1\\
0
\end{pmatrix} = \begin{pmatrix}
0\\
1
\end{pmatrix} \nonumber \]
\[ A \begin{pmatrix}
0\\
1
\end{pmatrix} = \begin{pmatrix}
1\\
0
\end{pmatrix} \nonumber \]
\[ N \begin{pmatrix}
1\\
0
\end{pmatrix} = \begin{pmatrix}
0\\
0
\end{pmatrix} \nonumber \]
\[ N \begin{pmatrix}
0\\
1
\end{pmatrix} = \begin{pmatrix}
0\\
1
\end{pmatrix} \nonumber \]
The creation operator is the Hermitian adjoint of the annihilation operator and the annihilation operator is the Hermitian adjoint of the creation operator.
\[ \overline{(A^T)} = \begin{pmatrix}
0 & 0\\
1 & 0
\end{pmatrix} \nonumber \]
\[ \overline{(C^T)} = \begin{pmatrix}
0 & 1\\
0 & 0
\end{pmatrix} \nonumber \]
The number operator is the product of the creation and annihilation operators.
\[ CA = \begin{pmatrix}
0 & 0\\
0 & 1
\end{pmatrix} \nonumber \]
\[ \overline{(A^T)} A = \begin{pmatrix}
0 & 0\\
0 & 1
\end{pmatrix} \nonumber \]
\[ \overline{(C^T)} C = \begin{pmatrix}
0 & 0\\
0 & 1
\end{pmatrix} \nonumber \]
The eigenvectors of the number operator are |0> and |1> with eigenvalues 0 and 1, respectively:
\[ eigenvecs(N) = \begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix} \nonumber \]
\[ eigenvals(N) = \begin{pmatrix}
0\\
1
\end{pmatrix} \nonumber \]
There are two paths to each detector. This provides the opportunity for constructive and destructive interference. To arrive at D1 the a-arm photon state is reflected (90 degree phase shift) at BS2 and the b-arm photon state is transmitted at BS2. Therefore, photon detection requires the annihilation of the superposition of these paths to D1. The annihilation is achieved with the following operator.
\[ \frac{iA_a + A_b}{ \sqrt{2}} \nonumber \]
The product of this operator with its Hermitian conjugate (see above) creates the number operator for photon detection at D1.
\[ N_{D1} = \frac{iC_a + C_b}{ \sqrt{2}} + \frac{iA_a + A_b}{ \sqrt{2}} \nonumber \]
The D1 number operator is formed using Mathcad's kronecker command as follows:
ND1 = \( \frac{1}{2}\) (-i kronecker (C, I) + kronecker (I, C)) (i kronecker (A,I) + kronecker (I, A))
To arrive at D2 the a-arm photon state is transmitted at BS2 and the b-arm photon state is reflected (90 degree phase shift) at BS2. Photon detection at D2 requires the annihilation of the superposition of these paths to the detector. The annihilation is represented the following operator.
\[ \frac{iA_a + A_b}{ \sqrt{2}} \nonumber \]
Therefore, the number operator for photon detection at D2 is:
\[ N_{D2} = \frac{C_a + iC_b}{ \sqrt{2}} \frac{A_a + iA_b}{ \sqrt{2}} \nonumber \]
The D2 number operator is formed using Mathcad's kronecker command as follows.
ND2 = \( \frac{1}{2}\) (kronecker (C, I) - i kronecker (I, C)) (kronecker (A,I) + i kronecker (I, A))
We now show that the photon always arrives at D1 and never at D2 for an equal arm MZI.
Expectation value for photon detection at D1:
\[ \overline{ \Psi ^T} N_{D1} \Psi = 1 \nonumber \]
Expectation value for photon detection at D2:
\[ \overline{ \Psi ^T} N_{D2} \Psi = 1 \nonumber \]
Equivalent results can be obtained algebraically. Operating on \( \Psi\) with the D1 number operator yields \( \Psi\). In other words, \( \Psi\) is an eigenfunction of ND1 with eigenvalue 1.
\[ \bigg[ \frac{-C_a + C_b}{ \sqrt{2}} \frac{iA_a + A_b}{\sqrt{2}} \bigg] \frac{1}{ \sqrt{2}} \big[ |1 \rangle_a |0 \rangle_b + i|0 \rangle_a |1 \rangle_b \big] = \frac{1}{ \sqrt{2}} \big[ |1 \rangle_a |0 \rangle_b + i|0_a |1 \rangle_b \big] \nonumber \]
Operating on \( \Psi\) with the D2 number operator yields 0.
\[ \bigg[ \frac{C_a - iC_b}{ \sqrt{2}} \frac{A_a + iA_b}{\sqrt{2}} \bigg] \frac{1}{ \sqrt{2}} \big[ |1 \rangle_a |0 \rangle_b + i|0 \rangle_a |1 \rangle_b \big] = 0 \nonumber \]

