7.1: Single-Photon Interference - First Version
- Page ID
- 137746
The schematic diagram below shows a Mach-Zehnder interferometer for photons. When the experiment is run so that there is only one photon in the apparatus at any time, the photon is always detected at \(D_2\) and never at \(D_1\).(1,2,3) The qualitative explanation is that there are two paths to each detector and, therefore, the probability amplitudes for these paths may interfere constructively or destructively. For detector \(D_2\) the probability amplitudes for the two paths interfere constructively, while for detector \(D_1\) they interfere destructively.
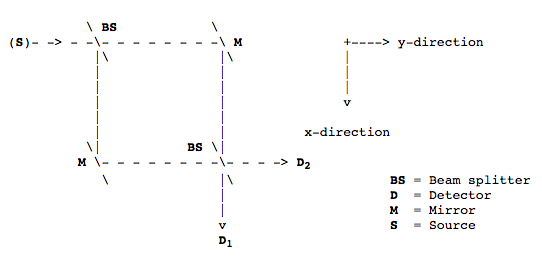
A quantitative quantum mechanical analysis of this striking phenomenon is outlined below. The photon leaves the source, S, traveling in the y-direction. Whether the photon takes the upper or lower path it interacts with a beam splitter, a mirror, and another beam splitter before reaching the detectors.
Orthonormal basis states: (1 x 2 vectors)
Photon moving in the x-direction: \( | x > = \begin{vmatrix}
1\\
0
\end{vmatrix}~~~< x | = (1~~~0)~~~< x | x > = 1\)
Photon moving in the y-direction: \( | y > = \begin{vmatrix}
0 \\
1
\end{vmatrix}~~~< y | = (0~~~1) ~~~< y | y > = 1\)
< y | x > = < x | y > = 0
Operators: (2 x 2 matrices)
Operator for photon interaction with the mirror:
\[ \hat{M} = \( \begin{vmatrix} 0 & 1\\ 1 & 0 \end{vmatrix} \nonumber \]
Operator for photon interaction with the beam splitter:
\[\hat{BS} = \(\begin{vmatrix} T & iR\\ iR & T \end{vmatrix} \nonumber \]
\(T\) and \(R\) are the transmission and reflection amplitudes. For the half-silvered mirrors used in this example they are:
\[ T = R = \left( \dfrac{1}{2} \right) ^{ \frac{1}{2}} = 0.707 \nonumber \]
Operations:
After interacting with a beam splitter, a photon is in a linear superposition of |x> and |y> in which the components are 90 degrees out of phase.
\[\hat{BS}|x \rangle = \dfrac{[ |x + i|y]}{2}^{ \frac{1}{2}} \nonumber \]
\[\hat{BS}|y \rangle = \dfrac{[ i|x + i|y]}{2}^{ \frac{1}{2}} \nonumber \]
BS M BS|y > = i|y>
Interaction with the mirror merely changes the direction of the photon.
\[\hat{M} | x \rangle = | y \rangle \nonumber \]
\[\hat{M} | y \rangle = | x \rangle \nonumber \]
Matrix elements:
< x | M | x > = 0 < y | M | x > = 1 < x | M | y > = 1 < y | M | y > = 0
< x | BS | x > = < y | BS | y > = \( \frac{1}{2}^{ \frac{1}{2}}\) < y | BS | x > = < x | BS | y > = \( \frac{i}{2}^{ \frac{1}{2}}\)
Dirac brackets are read from right to left. In Dirac's notation < x | M | y > is the amplitude that a photon initially moving in the y-direction will be moving in the x-direction after interacting with the mirror. |< x | M | y >|2 is the probability that a photon initially moving in the y-direction will be moving in the x-direction after interacting with the mirror. |< y | BS | y >|2 is the probability that a photon initially moving in the y-direction will be found moving in the y-direction after interacting with the beam splitter.
(A) For the photon to be detected at D1 it must be in the state |x> after interacting with two beam splitters and a mirror in the configuration shown above. The probability that a photon will be detected at D1:
< x | BS M BS | y > = 0 thus |< x | BS M BS |y>|2 = 0
(B) For the photon to be detected at D2 it must be in the state |y> after interacting with two beam splitters and a mirror in the configuration shown above. The probability that a photon will be detected at D2:
< y |BS M BS| y > = i thus |< y |BS M BS| y >|2 = 1
It is also instructive to use Dirac's notation to examine upper and lower paths.
(A')
\[\begin{align} \langle D_1| y \rangle &= \langle D_1 | y \rangle_{upper} + \langle D_1 | y \rangle_{lower} \\[4pt] &= \langle x | \textbf{BS} | x \rangle\langle x | \textbf{M} | y \rangle\langle y | \textbf{BS} | y \rangle + \langle x | \textbf{BS} | y \rangle\langle y | \textbf{M} | x \rangle\langle x | \textbf{BS} | y > \\[4pt] &= \frac{i}{2}^{ \frac{1}{2}} \times 1 \times \frac{i}{2}^{ \frac{1}{2}} + \frac{i}{2}^{ \frac{1}{2}} \times 1 \times \frac{i}{2}^{ \frac{1}{2}} \\[4pt] &= \frac{i}{2} - \frac{i}{2} = i \end{align} \nonumber \]
This shows that upper and lower paths have the photon arriving 180 degrees out of phase. Thus the photon suffers destructive interference at D1.
(B') < D2 | y > = < D2 | y >upper + < D2 | Y >lower
= < y | BS | x >< x | M | y >< y | BS | y > + < y | BS | y >< y | M | x >< x | BS | y >
= \( \frac{i}{2}^{ \frac{1}{2}} \times 1 \times \frac{i}{2}^{ \frac{1}{2}}\) + \( \frac{i}{2}^{ \frac{1}{2}} \times 1 \times \frac{i}{2}^{ \frac{1}{2}}\)
= \( \frac{i}{2} - \frac{i}{2} = i\) i
Thus, |< D2 | y >|2 = 1
This calculation shows that the upper and lower paths have the photon arriving in phase at D2.
If either path (upper or lower) is blocked the interference no longer occurs and the photon reaches D1 25% of the time and D2 25%. Of course, 50% of the time it is absorbed by the blocker.
Lower path blocked:
Probability photon reaches D1: |< x | BS | x >< x | M | y >< y | BS | y >|2 = \( \frac{1}{4}\)
Probability photon reaches D2: |< y | BS | x >< x | M | y >< y | BS | y >|2 = \( \frac{1}{4}\)
Upper path blocked:
Probability photon reaches D1: |< x | BS | y >< y | M | x >< x | BS | y >|2 = \( \frac{1}{4}\)
Probability photon reaches D2: |< y | BS | y >< y | M | x >< x | BS | y >|2 = \( \frac{1}{4}\)
References:
- P. Grangier, G. Roger, and A. Aspect, "Experimental Evidence for Photon Anticorrelation Effects on a Beam Splitter: A New Light on Single Photon Interferences," Europhys. Lett. 1, 173-179 (1986).
- V. Scarani and A. Suarez, "Introducing Quantum Mechanics: One-particle Interferences," Am. J. Phys. 66, 718-721 (1998).
- Kwiat, P, Weinfurter, H., and Zeilinger, A, "Quantum Seeing in the Dark," Sci. Amer. Nov. 1996, pp 72-78.

