9.21: Numerical Solutions for the Hydrogen Atom Radial Equation
- Page ID
- 137744
Reduced mass: \( \mu\) = 1
Angular momentum: L = 0
Integration limit: rmax = 18
Nuclear charge: Z = 1
Solve Schrödinger's equation numerically. Use Mathcad's ODE solve block:
Given
\[ \frac{-1}{2 \mu} \frac{d^2}{dr^2} \psi (r) - \frac{1}{r \mu} \frac{d}{dr} \psi (r) + \bigg[ \frac{L( L + 1)}{2 \mu r^2} + \frac{1}{2} kr^2 \bigg] \psi (r) = E \psi (r)~~~ \psi (.0001) = .1~~~ \psi '(.0001) = 0.1 \nonumber \]
\[ \psi = Odesolve (r, r_{max}) \nonumber \]
Normalize wave function:
\[ \psi (r) = \left( \int_{0}^{r_{max}} \psi (r)^2 4 \pi r^2 dr \right) ^{ \frac{-1}{2}} \psi (r) \nonumber \]
Energy guess:
E = -.125 r = 0, .001 .. rmax
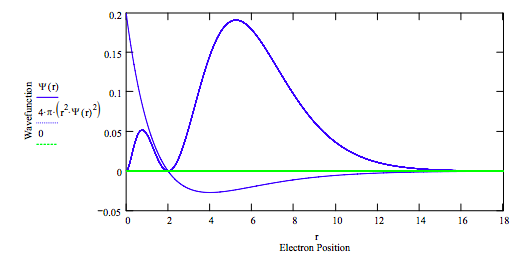
Calculate average position:
\[ \int_{0}^{r_{max}} \psi (r) r \psi (r) 4 \pi r^2 dr = 5.997 \nonumber \]
Calculate kinetic energy:
\[ \int_{0}^{r_{max}} \psi (r) \bigg[ \frac{-1}{2 \mu} \frac{d^2}{dr^2} \psi (r) - \frac{1}{r \mu} \frac{d}{dr} \psi (r) + \bigg [ \frac{L(L + 1)}{2 \mu r^2} \bigg] \psi (r) \bigg] 4 \pi r^2 dr = 0.125 \nonumber \]
Calculate potential energy:
\[ \int_{0}^{r_{max}} \psi (r) \frac{-Z}{r} \psi (r) 4 \pi r^2 dr = -0.25 \nonumber \]

