11.18: Cosmic Background Radiation
- Page ID
- 135893
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
The cosmic background radiation fills all space and is a relic from the "big bang" that created the universe approximately 18 billion years ago. The data1 shown below, spectral brightness2 as a function of wave number, was recorded (1989) by the Cosmic Background Explorer satellite (COBE). Below the data is fit with the Planck blackbody radiation equation to determine the cosmic background temperature.
Define the fundamental constants h, k, and c.
h := 6.62608 ⋅ 10-34 k := 1.380622 ⋅ 10−23 c := 2.99792458 ⋅ 108
νi := 100 ⋅ νi Bi := 10−18 ⋅ Bi
Provide a seed value for the background temperature: T := 10
Define spectral brightness equation:
\[ F(\nu , T) := 2 \cdot h \cdot \nu ^{3} \cdot c \cdot \frac{1}{(exp( \frac{ h \cdot \nu}{k \cdot T}) - 1)} \nonumber \]
SSD stands for sum of the square of the deviations between data and the equation that is being fit to the data.
\[SSD(T) = \sum_{i} (B_{i} - F (\nu _{i}, T))^{2} \nonumber \]
Given SSD(T) := 0 T := Minerr(T) T := 2.728
Thus the best fit to the data is obtained with a cosmic background temperature of 2.728 K.
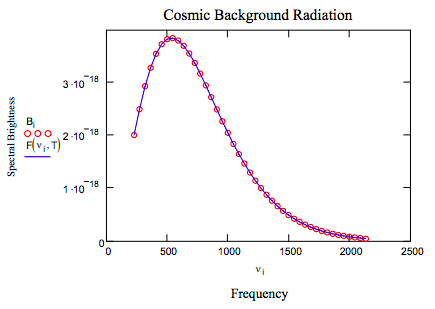
Notes:
1. Data taken from: S. Bluestone, JCE 78, 215-218 (2001).
2. The relationship between spectral brightness and Planck's radiation density function is:
\( B( \nu , T) = \frac{c}{4 \cdot \pi} \cdot \rho ( \nu, T)\)
n := 43 i := 1 .. n
\( \nu_{i}\) :=
\( \begin{array}{|r|}
\hline \\
2.27 \\
\hline \\
2.72 \\
\hline \\
3.18 \\
\hline \\
3.63 \\
\hline \\
4.08 \\
\hline \\
4.54 \\
\hline \\
4.99 \\
\hline \\
5.45 \\
\hline \\
5.90 \\
\hline \\
6.35 \\
\hline \\
6.81 \\
\hline \\
7.26 \\
\hline \\
7.71 \\
\hline \\
8.17 \\
\hline \\
8.62 \\
\hline \\
9.08 \\
\hline \\
9.53 \\
\hline \\
9.98 \\
\hline \\
10.44 \\
\hline \\
10.89 \\
\hline \\
10.89 \\
\hline \\
11.34 \\
\hline \\
11.80 \\
\hline \\
12.25 \\
\hline \\
12.71 \\
\hline \\
13.16 \\
\hline \\
13.61 \\
\hline \\
14.07 \\
\hline \\
14.52 \\
\hline \\
14.97 \\
\hline \\
15.43 \\
\hline \\
15.88 \\
\hline \\
16.34 \\
\hline \\
16.79 \\
\hline \\
17.24 \\
\hline\\
17.70 \\
\hline \\
18.15 \\
\hline \\
18.61 \\
\hline \\
19.06 \\
\hline \\
19.51 \\
\hline \\
19.97 \\
\hline \\
20.42 \\
\hline \\
20.87 \\
\hline \\
21.33 \\
\hline
\end{array} \)
Bi :=
\( \begin{array}{|r|}
\hline \\
2.0110 \\
\hline \\
2.5003 \\
\hline \\
2.9369 \\
\hline \\
3.2858 \\
\hline \\
3.5503 \\
\hline \\
3.7316 \\
\hline \\
3.8269 \\
\hline \\
3.8477 \\
\hline \\
3.8027 \\
\hline \\
3.7025 \\
\hline \\
3.5551 \\
\hline \\
3.3773 \\
\hline \\
3.1752 \\
\hline \\
2.9535 \\
\hline \\
2.7281 \\
\hline \\
2.4957 \\
\hline \\
2.2721 \\
\hline \\
2.0552 \\
\hline \\
1.8483 \\
\hline \\
1.6488 \\
\hline \\
1.4672 \\
\hline \\
1.2973 \\
\hline \\
1.1438 \\
\hline \\
1.0019 \\
\hline \\
0.8771 \\
\hline \\
0.7648 \\
\hline \\
0.6631 \\
\hline \\
0.5749 \\
\hline \\
0.4965 \\
\hline \\
0.4265 \\
\hline \\
0.3669 \\
\hline \\
0.3136 \\
\hline \\
0.2684 \\
\hline \\
0.2287 \\
\hline \\
0.1945 \\
\hline\\
0.1657 \\
\hline \\
0.1396 \\
\hline \\
0.1185 \\
\hline \\
0.1003 \\
\hline \\
0.0846 \\
\hline \\
0.0717 \\
\hline \\
0.0587 \\
\hline \\
0.0459 \\
\hline
\end{array} \)

