11.14: The Global Approach to Thermodynamics
- Page ID
- 135510
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Thermodynamics: Energy conservation with an entropy-based limitation on energy utilization. Nick Herbert
Cochran and Heron recently published an assessment of student ability to apply the laws of thermodynamics to heat engines and refrigerators with special emphasis on the second law.1 They reported exam question results for three levels of instruction: (a) standard; (b) standard plus a tutorial on Carnot’s theorem; (c) standard plus a tutorial on the use of the entropy inequality. The performance of students exposed to instruction levels (b) and (c) was significantly better than that for students who had only the standard level of instruction.
The three levels of instruction all use the system-centered approach to thermodynamics. I would like to propose that a future study include another option – the global approach to thermodynamics.2 In the global approach, after a sketch of the phenomenon under study is made, the sums of the energy and entropy changes are calculated.
\( \Delta E_{tot} = \sum_{i} \Delta E_{i}\) \( \Delta S_{tot} = \sum_{i} \Delta S_{i}\)
Thermodynamics requires that \( \Delta E_{tot} = 0\) and \( \Delta S \geq 0\) for all phenomena.
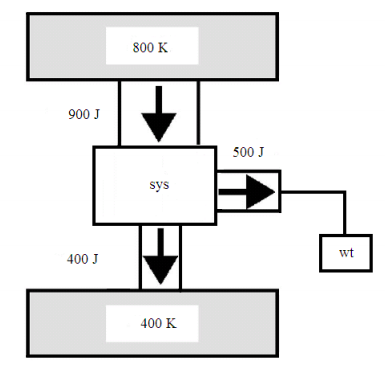
The global method will be illustrated by applying it to the heat engine shown in the figure, which is the same heat engine as shown in Figure 2 of reference 1. As shown in the appended figure, work is represented by a weight which can rise or fall in the gravitational field.
The global statement of the first law is
\( \Delta E_{tot} = \Delta E_{800} + \Delta E_{sys} + \Delta E_{400} + \Delta E_{wt}\)
Because the working substance of the system completes a thermodynamic cycle, \( \Delta E_{sys} = 0\). Using the energy values in the figure we find that the first law is satisfied; energy is conserved.
\( \Delta E_{tot} = -900J + 0J + 400J + 500J = 0\)
In the global statement for the second law is
\( \Delta S_{tot} = \Delta S_{800} + \Delta S_{sys} + \Delta S_{400} + \Delta S_{wt}\)
For thermal reservoirs \( \Delta S = \frac{ \Delta E_{T}}{T}\), where \( \Delta E_{T}\) is the thermal energy change of a reservoir at temperature T. Again, because the working substance undergoes a thermodynamic cycle, \( \Delta S_{sys} = 0\). The movement of a weight in a gravitational field does not change its entropy, therefore, \( \Delta S_{wt} = 0\).
Using the information from the figure we calculate a negative value for the total entropy change, indicating that a heat engine operating under these conditions is not possible.
\( \Delta S_{tot} = \frac{-900J}{800K} + 0 \frac{J}{K} + \frac{400J}{400K} + 0 \frac{J}{K} = -0.125 \frac{J}{K}\)
By comparison with this global analysis, Cochran and Heron use an auxiliary thermodynamic function, the entropy inequality, to arrive at the same conclusion.
\( \Delta S_{sys} \geq \sum \frac{Q_{to~sys}}{T_{env}} = \frac{900 J}{800K} - \frac{400 J}{400 K} = 0.125 \frac{J}{K}\)
This result contradicts the fact that a cyclic process for the system’s working substance requires that \( \Delta S_{sys} = 0\). Therefore, the proposed heat engine will not function. However, this method is less direct because the entropy inequality is an auxiliary thermodynamic function which is derived from the second law of thermodynamics.
Employing a global thermodynamic analysis of the other figures shown in reference 1, as well as other types of physical and chemical phenomena is straightforward.2
It is, of course, important to explore the limits thermodynamics places on the performance of heat engines and refrigerators. These limits can be obtained from the global statements of the first and second laws of thermodynamics by elementary mathematical methods. For traditional heat engines and refrigerators (two thermal reservoirs) the first and second laws are,
\( \Delta E_{hot} + \Delta E_{cold} + \Delta E_{wt} = 0\)
\( \frac{ \Delta E_{hot}}{T_{hot}} + \frac{ \Delta E_{cold}}{T_{cold}} \geq 0\)
Using the first law to eliminate ΔEcold in the equation for the second law yields the efficiency relation for heat engines.
\( \varepsilon = \frac{ \Delta E_{wt}}{ - \Delta E_{hot}} \leq 1 - \frac{T_{cold}}{T_{hot}}\)
Using the first law to eliminate \( \Delta E_{hot}\) in the equation for the second law yields the coefficient of performance for refrigerators.
\( \kappa = \frac{- \Delta E_{cold}}{ \Delta E_{wt}} \leq \frac{T_{cold}}{T_{hot} - T_{cold}}\)
The most appealing feature of the non-system centered, global approach to thermodynamics is that the first and second laws are front and center, starring you in the face, and not represented by surrogates. Another important feature is not to have to subscript terms involving thermal energy and work with “to sys” and “on sys”. Each part of the phenomenon under study carries its own label; the system is just another part, neither more nor less important than any other part.
1M. J. Cochran and P. R. L. Heron, “Development and assessment of research-based tutorials on heat engines and the second law of thermodynamics,” Am. J. Phys. 74, 734- 741 (2006).
2H. A. Bent, The Second Law: An Introduction to Classical and Statistical Thermodynamics (Oxford University Press, New York, 1965).