3.31: Quantum Mechanics, Group Theory and C60
- Page ID
- 154838
The recent discovery of a new allotropic form of carbon1 and its production in macroscopic amounts2 has generated a tremendous amount of research activity in chemistry, physics and material science.3 Among the areas of current interest are the electronic properties of the fullerenes and this note describes a simple model for the electronic structure of Coo that is consistent with recent experimental findings. It is based on the most elementary principles of quantum mechanics and group theory.
After the soccer-ball structure for C60 was first suggested in 1985 it became important to obtain as much independent supporting evidence as possible. This came in the areas of nmr, IR, and Raman spectroscopy. The nmr spectrum showed a single resonance indicating 60 equivalent carbon atoms in the structure. The IR spectrum was found to have four lines, while Raman spectroscopy yielded ten lines. The second half of this paper will use group theory to demonstrate that a C60 molecule with a soccer-ball structure must have four IR active and ten Raman active vibrational modes.
Electronic Structure
As is well-known C60 is a carbon cage consisting of 20 hexagons and 12 pentagons and resembles a soccerball. Removing the leather, but keeping the seams, leaves 60 vertices for the carbon atoms and 90 covalent bonds between them. Actually C60 has spheroidal geometry and belongs to the truncated icosahedral symmetry group, lh. Curly and Smalley, codiscoverers of buckminsterfullerene, have described it as the "roundest molecule that can possibly exist"4 so the model presented here assumes, initially, that Coo is a perfect sphere. Each carbon is sigma bonded to three other carbons using three of its four valence electrons to form these bonds. The remaining electron is considered to be delocalized on the surface of the sphere created by the 60 atom carbon cage.
The quantum mechanical behavior of an individual electron restricted to the surface of a sphere is well-known.5 Solving Schrödinger's equation for a particle on a sphere yields the spherical harmonic wavefunctions, pictures of which can be found in Atkins' physical chemistry textbook. The energy levels associated with the spherical harmonic states are a function of the radius of the sphere and the angular momentum quantum number.
\[ E_L = \frac{h^2}{8 \pi^2 m_e R^2} L(L+1) \nonumber \]
Just as the quantum mechanical solution for the one-electron hydrogen atom can be adapted for qualitative treatments of the electronic structure of multi-electron atoms, so the energy level diagram for the electron moving on a sphere can be used to describe the electronic structure of C60. The energy level diagram shown in Figure 1 provides a qualitative description of the electronic structure obtained when one applies the aufbau principle, the Pauli exclusion principle, and Hund' s rule to the addition of 60 electrons to the available spherical harmonic energy levels.

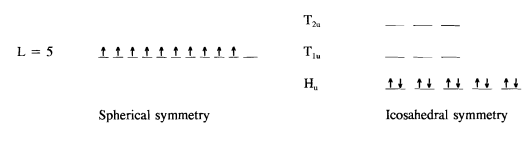
As it stands this is not a satisfactory picture because pristine C60 is an insulator and has no un-paired electrons. This difficulty is resolved by recalling that C60 is not a perfect sphere, but has the lower symmetry of the icosahedral group. Invoking icosahedral symmetry at this point splits the degeneracies of all levels above L = 2. However, initially it is only necessary to examine what happens to the highest occupied level, L = 5, since all other levels are completely filled.
Using traditional group theoretical methods6, it can be shown that the L = 5 spherical harmonics transform under the rotations of the icosahedral symmetry group as shown in the last row of the icosahedral character table shown below. The behavior of the spherical harmonics under the rotations of the icosahedral group is given by
\[ \chi \left( c_{ \alpha} \right) = \frac{ \sin \left( L + \frac{1}{2} \right) \alpha}{ \sin \frac{ \alpha}{2}} \nonumber \]
| Ih | E | 12C5 | 12C52 | 20C3 | 15C2 |
| A | 1 | 1 | 1 | 1 | 1 |
| T1 | 3 | 1.618 | -.618 | 0 | -1 |
| T2 | 3 | -.618 | 1.618 | 0 | -1 |
| G | 4 | -1 | -1 | 1 | 0 |
| H | 5 | 0 | 0 | -1 | 1 |
| L=5 | 11 | 1 | 1 | -1 | -1 |
It is easy to show that this reducible representation is a linear combination of the fivefold degenerate Hu, an the two three-fold degenergate, T1u and T2u irreducible representations of the icosahedral group. Group theory doesn't predict the order of the levels, but Figure 2 shows that if the five-fold degenerate level is placed lowest, an energy level diagram that captures the essentials of the known electronic structure of C60 is obtained.7,8 This assignment is consistent with HOMO, LUMO, and LUMO+ 1 levels of the Huckel molecular orbital calculation on C60.8,9 In addition, if the splittings of the L = 3 and L = 4 states are also examined in the manner outlined above, the complete energy level diagram for the π-electrons of C60 shown in Figure 3 is obtained. This set of π-electron levels is qualitatively consistent with the results of an ab initio calculation based on the pseudopotentiallocal density method.10

The HOMO-LUMO energy gap is known to be 1.5 eV. However, the HOMO -> LUMO electronic transition is optically forbidden. Because Hu level is full, (Hu)10, the ground electronic state has Ag symmetry. The first excited state (Hu)9(T1u)1 produces the reducible representation shown in the table below. This is obtained by taking the direct product of the Hu and T1u irreducible representations (HuxT1u). The reducible representation of the second excited state, (Hu)9(T1g)1 is also shown in the table. It is important to note that both excited states are 15-fold degenerate.
| E | 12C5 | 12C52 | 20C3 | 15C2 | i | 12S10 | 12S102 | 20S6 | 15
σ |
|
| HuT1u | 15 | 0 | 0 | 0 | -15 | 15 | 0 | 0 | 0 | 15 |
| HuT1g | 15 | 0 | 0 | 0 | -15 | -15 | 0 | 0 | 0 | 15 |
Employing the usual methods it is not difficult to show that the first and second excited electronic configurations contain the following irreducible representations.
\[ \begin{matrix} \left( H_u \right)^9 \left(T_{1u} \right)^1 \rightarrow T_{1g} + T_{2g} + G_g + H_g \\ \left( H_u \right)^9 \left( T_{1g} \right)^1 \rightarrow T_{1u} + T_{2u} + G_u + H_u \end{matrix} \nonumber \]
Thus, it can be seen that the excited electronic configurations each give rise to four excited states. In order for a transition to any of these states from the ground state to be allowed, the transition probability integral ∫ΨiμΨfdτ must be non-zero. For this integral to be non-zero the direct product of the irreducible representations for the ground electronic state, the electric dipole operator, and the excited electronic state must contain the totally symmetric irreducible representation Ag. Because the ground state itself has Ag symmetry and the electric dipole operator has T1u symmetry, only an excited state with T1u symmetry will lead to a direct product which contains the Ag irreducible representation.
Inspection of the irreducible representations for the first and second exited electronic configurations shows that only the second excited electronic configuration contains the T1u irreducible representation. Thus, while the HOMO → LUMO transition is forbidden, the HOMO → LUMO+ 1 transition is allowed. This result is consistent with the visible spectrum of the free molecule.9
A further comment on the magnitude of the HOMO-LUMO gap might be made at this point. The energies of the spherical harmonic states shown in Figure 1 were calculated using equation (1) and a value of 710 pm for the diameter of the carbon cage. At the L = 5 level the energy difference between adjacent states is 3.1 and 3.6 eV. While the model doesn't provide a detailed quantitative analysis of.the splitting of the L = 5 level, using reasonable assumptions one can obtain a value for the HOMO-LUMO gap that is "in the ball park. "
In summary, this analysis provides a simple interpretation of the fact that C60 is an insulator. The model also provides low-lying, un-occupied orbitals to form conduction bands and receive electrons from donors such as potassium. Furthermore, the fact that the LUMO is triply degenerate is consistent with the experimental evidence that K3C60 is a conductor and K6C60 is an insulator.7 While this simple model is not a rival to the more sophisticated molecular orbital or band theory calculations, it does provide the non-specialist with an appealing and simple alternative.
Vibrational Spectroscopy
To analyze the vibrational modes of C60 using group theory it is necessary to determine how the 180 degrees of freedom of the C60 molecule transform under the symmetry operations of the Ih group. This is actually quite easily done because the rotations and the inversion symmetry operation move all the carbon atoms and, therefore, have characters of O. The identity operation leaves all carbons unmoved for a character of 180, while the 15 planes of symmetry contain four carbon atoms each and can be shown to have a character of 4. The model of C60 on the first page shows one of these planes. It is perpendicular to the plane of the paper and clearly contains four carbon atoms, two at the top and two at the bottom.
This makes it very easy to decompose the reducible representation, Γtot, into its irreducible representations by the usual methods. This is summarized in the table on the next two pages. For simplicity only the E and cr symmetry operations are shown, but it must be remembered that there are 120 symmetry operations total. For example, the occurrence of Hg is calculated as follows:
\[ \Lambda_{tot} \cdot H_g = \frac{[(1)(180)(5)+(15)(4)(1)]}{120} = 8 \nonumber \]
After translation and rotation are subtracted from the total, 174 vibrational degrees of freedom remain. However, group theory shows that many vibrational modes are degenerate. In fact, as the table below shows, there are only 46 distinct vibrational frequencies.
\[ \Lambda_{vib} = 2A_g + 3T_{1g} + 4T_{2g} + 6G_g + 8H_g + A_u + 4T_{1u} + 5T_{2u} + 6G_u + 7H_u \nonumber \]
Of these, the table indicates that only the four triply degenerate T1u modes are IR active while ten vibrational modes (2Ag + 8Hg) are Raman active. This analysis is in complete agreement with the experimental measurements11 and was considered to be crucial evidence in support of the proposed soccer-ball structure for C60. Several of the rotational axes for C60 are shown below to illustrate that they do move all atoms.
| Ih | E | 15σ | Occurrence | h = 120 |
|
Γxyz |
180 | 4 | ||
| Ag | 1 | 1 | 2 | Raman active |
| T1g | 3 | -1 | 4 | Rx, Ry, Rz |
| T2g | 3 | -1 | 4 | |
| Gg | 4 | 0 | 6 | |
| Hg | 5 | 1 | 8 | Raman active |
| Au | 1 | -1 | 1 | |
| T1u | 3 | 1 | 5 | Tx, Ty, Tz /IR |
| T2u | 3 | 1 | 5 | |
| Gu | 4 | 0 | 6 | |
| Hu | 5 | -1 | 7 |
Literature cited:
- Kroto, H. W.; Heath, J. R.; O'Brien, S. C.; Curl, R. F.; Smalley, R. E. Nature 1985, 318, 162-164.
- Kratschmer, W.; Lamb, L. D.; Fostiropolous, K.; and Huffman, D. R., Nature 1990, 347, 354.
- Accounts of Chemical Research 1992, 25 , number 3.
- Curl, R.F.; Smalley, R. E. Sci. Am. 1991, 10, 54-63.
- Atkins, P. W. Physical Chemistry, 1990 (W. H. Freeman and Company, New York, 4th edition, Chapter 12, pages 336-338).
- Atkins, P. W. Molecular Quantum Mechanics, 1983 (Oxford University Press, Oxford, New York, 2nd Edition, Chapter 7, pages 163-167).
- Weaver, J. H., et al. Phys. Rev. Lett. 1991, 66, 1741-1744.
- Haddon, R. C., Accounts of Chemical·Research 1992, 25, 127-133.
- Hebard, A. F., Physics Today 1992, 11, 26-32.
- Martins, J. L.; Troullier, N.; Weaver, J. H., Chem. Phys. Lett. 1991, 180, 457-60.
- Chung, F.; Sternberg, S., American Scientist 1993, 81, 56-71.

