10.35: First Order Degenerate Perturbation Theory - the Stark Effect of the Hydrogen Atom

The n = 2 level of the hydrogen atom is 4‐fold degenerate with energy ‐0.125 E_h. In terms of the \(|nlm \rangle\) quantum numbers these states are \(|2,0,0\rangle\), \(|2,1,0\rangle\), \(|2,1,1 \rangle\), and \(| 2,2,-1 \rangle\). An electric field in the z‐direction splits the degeneracy because it mixes the \(2s\) and the \(2p_z\) orbitals creating one linear combination polarized in the direction of the field and an other polarized against the field.

What happens is that the \(s\) and \(p\) wavefunctions "mixed" to produce eigenstates that have shifted centers. This means the atom gets an induced electric dipole moment, whose interaction with the external field either lowers or raises the eigenenergy.

The \(|2,0,0\rangle\) wavfunction is spherically symmetric (left), while the \(|2,2,0 \rangle\) wavefunction has two lobes where the wavefunction has different signs. If the applied field is strong, then the eigenstates will be even mixtures of these, but with different phases.

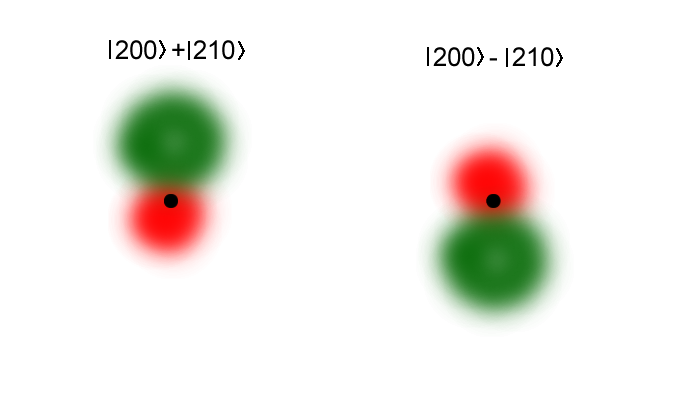
Note in particular that the electronic center of charge has moved from the origin, which means the states have nonzero dipole moments. With the electric field pointing downwards, the state to the left has a lower energy and the one to the right is raised.

Degenerate Perturbation Theory

The Hamiltonian for this perturbation in atomic units is:

\[H^{\prime}= εz, \nonumber \]

which in spherical polar coordinates is:

\[H^{\prime} = ε r\cos(θ), \nonumber \]

where \(ε\) is the electric field strength.

In this perturbation method treatment the hydrogen atom eigenfunctions are used to evaluate the matrix elements associated with the total Hamiltonian,

\[H = H^o + H^{\prime} \nonumber \]

Since the results for H^o are known (‐0.125 E_h) only the matrix elements for Hʹ need to be evaluated and most of these are zero. Below we show that = = ‐3ε and that the other matrix elements involving the \(n = 2\) orbitals are equal to zero.

\[ \psi_{2s} (r) = \frac{1}{ \sqrt{32 \pi}} (2-r) \exp \left( \frac{-r}{2} \right) \nonumber \]

\[ \psi_{2p_z} (r, \theta ) = \frac{1}{ \sqrt{32 \pi}} (r)\ exp \left( \frac{-r}{2} \right) \cos ( \theta ) \nonumber \]

\[ \psi_{2p_z} (r, \theta , \phi ) = \frac{1}{ \sqrt{32 \pi}} (r) \exp \left( \frac{-r}{2} \right) \sin ( \theta ) \cos ( \phi ) \nonumber \]

\[ \psi_{2p_z} (r, \theta , \phi ) = \frac{1}{ \sqrt{32 \pi}} (r) \exp \left( \frac{-r}{2} \right) \sin ( \theta ) \sin ( \phi ) \nonumber \]

\(\langle 2s | H^{\prime} | 2s \rangle = 0\)

\[ \int_{0}^{ \infty} \int_{0}^{ \pi} \int_{0}^{2 \pi} \psi_{2s} (r) \varepsilon r \cos ( \theta ) \psi_{2s} (r) r^2 \sin ( \theta ) d \pi d \theta dr \rightarrow 0 \nonumber \]

\(\langle 2p_z | H^{\prime} | 2p_z \rangle = \langle 2p_y | H^{\prime} | 2p_y \rangle = \langle 2p_x | H^{\prime} | 2p_x \rangle = 0\)

\[ \int_{0}^{ \infty} \int_{0}^{ \pi} \int_{0}^{2 \pi} \psi_{2pz} (r, \theta ) \varepsilon r \cos ( \theta ) \psi_{2pz} (r, \theta ) r^2 \sin ( \theta ) d \phi \,d \theta \,dr \rightarrow 0 \nonumber \]

\[ \int_{0}^{ \infty} \int_{0}^{ \pi} \int_{0}^{2 \pi} \psi_{2py} (r, \theta , \phi ) \varepsilon r \cos ( \theta ) \psi_{2py} (r, \theta , \phi ) r^2 \sin ( \theta ) d \phi \,d \theta \,dr \rightarrow 0 \nonumber \]

\[ \int_{0}^{ \infty} \int_{0}^{ \pi} \int_{0}^{2 \pi} \psi_{2px} (r, \theta , \phi ) \varepsilon r \cos ( \theta ) \psi_{2px} (r, \theta , \phi ) r^2 \sin ( \theta ) d \phi \,d \theta \,dr \rightarrow 0 \nonumber \]

\(\langle 2s | H^{\prime} | 2p_z \rangle = -3ε\)

\[ \int_{0}^{ \infty} \int_{0}^{ \pi} \int_{0}^{2 \pi} \psi_{2s} (r) \varepsilon r \cos ( \theta ) \psi_{2pz} (r, \theta ) r^2 \sin ( \theta ) d \phi \,d \theta \,dr \rightarrow -3 \varepsilon \nonumber \]

\(\langle 2s | H^{\prime} | 2p_x \rangle = \langle 2s | H^{\prime} | 2p_y \rangle = 0\)

\[ \int_{0}^{ \infty} \int_{0}^{ \pi} \int_{0}^{2 \pi} \psi_{2s} (r) \varepsilon r \cos ( \theta ) \psi_{2px} (r, \theta , \phi ) r^2 \sin ( \theta ) d \phi \,d \theta \,dr \rightarrow 0 \nonumber \]

\[ \int_{0}^{ \infty} \int_{0}^{ \pi} \int_{0}^{2 \pi} \psi_{2s} (r) \varepsilon r \cos ( \theta ) \psi_{2py} (r, \theta , \phi ) r^2 \sin ( \theta ) d \phi \,d \theta \,dr \rightarrow 0 \nonumber \]

\(\langle 2p_x | H^{\prime} | 2p_y \rangle = \langle 2p_x | H^{\prime} | 2p_z \rangle = \langle 2p_y | H^{\prime} | 2p_z \rangle = 0\)

\[ \int_{0}^{ \infty} \int_{0}^{ \pi} \int_{0}^{2 \pi} \psi_{2px} (r, \theta , \phi ) \varepsilon r \cos ( \theta ) \psi_{2py} (r, \theta , \phi ) r^2 \sin ( \theta ) d \phi \,d \theta \,dr \rightarrow 0 \nonumber \]

\[ \int_{0}^{ \infty} \int_{0}^{ \pi} \int_{0}^{2 \pi} \psi_{2px} (r, \theta , \phi ) \varepsilon r \cos ( \theta ) \psi_{2pz} (r, \theta ) r^2 \sin ( \theta ) d \phi \,d \theta \,dr \rightarrow 0 \nonumber \]

\[ \int_{0}^{ \infty} \int_{0}^{ \pi} \int_{0}^{2 \pi} \psi_{2py} (r, \theta , \phi ) \varepsilon r \cos ( \theta ) \psi_{2pz} (r, \theta ) r^2 \sin ( \theta ) d \phi \,d \theta \,dr \rightarrow 0 \nonumber \]

The matrix elements of the 4x4 perturbation matrix are

\[\langle ψ_i | H^o + H^{\prime} | ψ_j \rangle, \nonumber \]

where the ψʹs are the 2s, 2p_z, 2p_x, and 2p_y hydrogen atomic orbitals. Using the values of the integrals evaluated above the perturbation matrix is formed and its eigenvalues and eigenvectors found.

\[ \begin{pmatrix}
-0.125-E & -3 \varepsilon & 0 & 0 \\
-3 \varepsilon & -0.125-E & 0 & 0\\
0 & 0 & -0.125-E & 0\\
0 & 0 & 0 & -0.125-E
\end{pmatrix} \begin{pmatrix}
c_1\\
c_2\\
c_3\\
c_4
\end{pmatrix} = 0 \nonumber \]

This 4x4 energy matrix is clearly one 2x2 and two 1x1 energy matrices. In other words, as we learned from evaluating the matrix elements, the 2p_x and 2p_y are not perturbed by the electric field to first order and have energy ‐0.125 E_h.

The eigenvectors and eigenvalues of the 2x2 are found as follows.

\[\begin{bmatrix}
(-0.125-E)c_1-3 \varepsilon c_2 = 0)\\
-3 \varepsilon c_1 + (-0.125 - E) c_2 = 0)\\
c_1^2 + c_2^2 = 1
\end{bmatrix} |_{float,~3}^{solve,~\begin{pmatrix}
c_1\\
c_2\\
E
\end{pmatrix}} \rightarrow \begin{pmatrix}
-0.707 & 0.707 & 3.0 \varepsilon-0.125 \\
0.707 & -0.707 & 3.0 \varepsilon-0.125 \\
0.707 & 0.707 & -3.0 \varepsilon-0.125 \\
-0.707 & -0.707 & -3.0 \varepsilon-0.125
\end{pmatrix} \nonumber \]

The wavefunctions of the perturbed 2s and 2p_z orbitals are sp_z hybrid states as shown below.

\[ \frac{1}{ \sqrt{2}} (2s + 2p_{z})~~~E = (-0.125 - 3 \varepsilon ) E_{h} \nonumber \]

\[ \frac{1}{ \sqrt{2}} (2s - 2p_{z})~~~E = (-0.125 + 3 \varepsilon ) E_{h} \nonumber \]

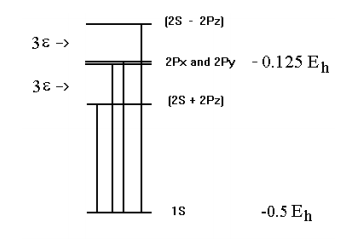
Because the energy of the symmetric 1s state is unaffected by the electric field, the effect of this perturbation on the electronic spectrum of hydrogen is to split the n = 1 to n = 2 transition into three lines of relative intensity 1:2:1.

< 2s | Hʹ | 2s > = 0

\[ \psi_{1s} (r) = \frac{1}{\sqrt{ \pi}} exp(-r) \nonumber \]

\[ \int_{0}^{ \infty} \int_{0}^{ \pi} \int_{0}^{2 \pi} \psi_{1s} (r) \varepsilon r \cos ( \theta ) \psi_{1s} (r) r^2 \sin ( \theta ) d \phi \,d \theta \,dr \rightarrow 0 \nonumber \]

Contributors and Attributions

• Prof. Emeritus Frank Rioux (St. John's University and College of St. Benedict)

• Emilio Pisanty via StackExchange (Physics)