Molecular Orbital Theory
- Page ID
- 8860
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Molecular orbital theory is a conceptual extension of the orbital model, which was so successfully applied to atomic structure. As was once playfully remarked, "a molecule is nothing more than an atom with more nuclei." This may be overly simplistic, but we do attempt, as far as possible, to exploit analogies with atomic structure. Our understanding of atomic orbitals began with the exact solutions of a prototype problem – the hydrogen atom. We will begin our study of homonuclear diatomic molecules beginning with another exactly solvable prototype, the hydrogen molecule-ion \(H_{2}^{+}\).
The Hydrogen Molecule-Ion
The simplest conceivable molecule would be made of two protons and one electron, namely \(H_{2}^{+}\). This species actually has a transient existence in electrical discharges through hydrogen gas and has been detected by mass spectrometry. It also has been detected in outer space. The Schrödinger equation forH\(H_{2}^{+}\) can be solved exactly within the Born-Oppenheimer approximation. For fixed internuclear distance R, this reduces to a problem of one electron in the field of two protons, designated A and B. We can write
\[\left\{-\dfrac{1}{2}\nabla^2\dfrac{1}{r_A}-\dfrac{1}{r_B}+\dfrac{1}{R} \right\} \psi(r)=E\psi(r) \label{1}\]
where rA and rB are the distances from the electron to protons A and B, respectively. This equation was solved by Burrau (1927), after separating the variables in prolate spheroidal coordinates. We will write down these coordinates but give only a pictorial account of the solutions. The three prolate spheroidal coordinates are designated \(\xi\), \(\eta\), \(\phi\). the first two are defined by
\[\xi=\dfrac{r_{A}+r_{B}}{R}\]
and
\[\eta=\dfrac{r_{A}-r_{B}}{R}\label{2}\]
while \(\phi\) is the angle of rotation about the internuclear axis. The surfaces of constant \(\xi\) and \(\eta\) are, respectively, confocal ellipsoids and hyperboloids of revolution with foci at A and B. The two-dimensional analog should be familiar from analytic geometry, an ellipse being the locus of points such that the sum of the distances to two foci is a constant. Analogously, a hyperbola is the locus whose difference is a constant. Figure \(\PageIndex{1}\) shows several surfaces of constant \(\xi\), \(\eta\) and \(\phi\). The ranges of the three coordinates are \(\xi\) \(\in\) \(\{1,\infty\}\), \(\eta\) \(\in\) \(\{-1,1\}\), \(\phi\) \(\in\) \(\{0,2\pi\}\). The prolate-spheroidal coordinate system conforms to the natural symmetry of the \(H_{2}^{+}\) problem in the same way that spherical polar coordinates were the appropriate choice for the hydrogen atom.
The first few solutions of the \(H_2^+\) Schrödinger equation are sketched in Figure \(\PageIndex{2}\), roughly in order of increasing energy. The \(\phi\)-dependence of the wavefunction is contained in a factor
\[\Phi(\phi)=e^{i\lambda\phi},\ \ \ \ \ \lambda=0,\pm1,\pm2,\ldots\label{3}\]
which is identical to the \(\phi\)-dependence in atomic orbitals. In fact, the quantum number \(\lambda\) represents the component of orbital angular momentum along the internuclear axis, the only component which has a definite value in systems with axial (cylindrical) symmetry. The quantum number \(\lambda\) determines the basic shape of a diatomic molecular orbital, in the same way that \(\ell\) did for an atomic orbital. An analogous code is used \(\sigma\) for \(\lambda\) = 0, \(\pi\) for \(\lambda\) = \(\pm\)1, \(\delta\) for \(\lambda\) = \(\pm\)2, and so on. We are already familiar with \(\sigma\)- and \(\pi\)-orbitals from valence-bond theory. A second classification of the \(H_{2}^{+}\) eigenfunctions pertains to their symmetry with respect to inversion through the center of the molecule, also known as parity. If \(\psi\)(-r) = +\(\psi\)(r), the function is classified gerade or even parity, and the orbital designation is given a subscript g, as in \(\sigma_{g}\) or \(\pi_{g}\). If \(\psi\)(-r) = -\(\psi\)(r), the function is classified as ungerade or odd parity, and we write instead \(\sigma_{u}\) or \(\pi_{u}\). Atomic orbitals can also be classified by inversion symmetry. However, all s and d atomic orbitals are g, while all p and f orbitals are u, so no further designation is necessary. The molecular orbitals of a given symmetry are numbered in order of increasing energy, for example, 1\(\sigma_{g}\), 2\(\sigma_{g}\), 3\(\sigma_{g}\).
The lowest-energy orbital, as we have come to expect, is nodeless. It obviously must have cylindrical symmetry (\(\lambda\) = 0) and inversion symmetry (g). It is designated 1\(\sigma_{g}\) since it is the first orbital of this classification. The next higher orbital has a nodal plane, with \(\eta\) = 0, perpendicular to the axis. This function still has cylindrical symmetry (\(\sigma\)) but now changes sign upon inversion (u). It is designated 1\(\sigma_{u}\), as the first orbital of this type. The next higher orbital has an inner ellipsiodal node. It has the same symmetry as the lowest orbital and is designated 2\(\sigma_{g}\). Next comes the 2\(\sigma_{u}\) orbital, with both planar and ellipsoidal nodes. Two degenerate \(\pi\)-orbitals come next, each with a nodal plane containing the internuclear axis, with \(\phi\)=const. Their classification is 1\(\pi_{u}\). The second 1\(\pi_{u}\)-orbital, not shown in Figure \(\PageIndex{2}\), has the same shape rotated by 90°. The 3\(\sigma_{g}\) orbital has two hyperbolic nodal surfaces, where \(\eta\) = \(\pm\)const. The 1\(\pi_{g}\), again doubly-degenerate, has two nodal planes, \(\eta\) = 0 and \(\phi\)=const. Finally, the 3\(\sigma_{u}\), the last orbital we consider, has three nodal surfaces where \(\eta\)=const.
An molecular orbital is classified as a bonding orbital if it promotes the bonding of the two atoms. Generally a bonding molecular orbital has a significant accumulation of electron charge in the region between the nuclei and thus reduces their mutual repulsion. The 1\(\sigma_{g}\), 2\(\sigma_{g}\), 1\(\pi_{u}\) and 3\(\sigma_{g}\) are evidently bonding orbitals. An molecular orbital which does not significantly contribute to nuclear shielding is classified as an antibonding orbital. The 1\(\sigma_{u}\), 2\(\sigma_{u}\), 1\(\pi_{g}\) and 3\(\sigma_{u}\) belong in this category. Often an antibonding molecular orbital is designated by \(\sigma\)* or \(\pi\)*.
The actual ground state of \(H_{2}^{+}\) has the 1\(\sigma_{g}\) orbital occupied. The equilibrium internuclear distance Re is 2.00 bohr and the binding energy De is 2.79 eV, which represents quite a strong chemical bond. The 1\(\sigma_{u}\) is a repulsive state and a transition from the ground state results in dissociation of the molecule.
The LCAO Approximation
In Figure \(\PageIndex{3}\), the 1\(\sigma_{g}\) and 1\(\sigma_{u}\) orbitals are plotted as functions of z, along the internuclear axis. Both functions have cusps, discontinuities in slope, at the positions of the two nuclei A and B. The 1s orbitals of hydrogen atoms have the same cusps. The shape of the 1\(\sigma_{g}\) and 1\(\sigma_{u}\) suggests that they can be approximated by a sum and difference, respectively, of hydrogen 1s orbitals, such that\[\psi(1\sigma_{g,u})\approx\psi(1s_{A})\pm\psi(1s_{B})\label{4}\]
This linear combination of atomic orbitals is the basis of the so-called LCAO approximation. The other orbitals pictured in Figure \(\PageIndex{2}\) can likewise be approximated as follows:
\[\psi(2\sigma_{g,u})\approx\psi(2s_{A})\pm\psi(2s_{B})\]
\[\psi(3\sigma_{g,u})\approx\psi(2p\sigma_{A})\pm\psi(2p\sigma_{B})\]
\[\psi(1\pi_{u,g})\approx\psi(2p\pi_{A})\pm\psi(2p\pi_{B})\label{5}\]
The 2\(p\sigma\) atomic orbital refers to 2pz, which has the axial symmetry of a \(\sigma\)-bond. Likewise 2\(p\pi\) refers to 2px or 2py, which are positioned to form \(\pi\)-bonds. An alternative notation for diatomic molecular orbitals which specifies their atomic origin and bonding/antibonding character is the following:
| 1\(\sigma_{g}\) | 1\(\sigma_{u}\) | 2\(\sigma_{g}\) | 2\(\sigma_{u}\) | 3\(\sigma_{g}\) | 3\(\sigma_{u}\) | 1\(\pi_{u}\) | 1\(\pi_{g}\) |
| \(\sigma\)1s | \(\sigma\)*1s | \(\sigma\)2s | \(\sigma\)*2s | \(\sigma\)2p | \(\sigma\)*2p | \(\pi\)2p | \(\pi\)*2p |
Almost all applications of molecular-orbital theory are based on the LCAO approach, since the exact \(H_{2}^{+}\) functions are far too complicated to work with.
The relationship between molecular orbitals and their constituent atomic orbitals can be represented in correlation diagrams, show in Figure \(\PageIndex{4}\).
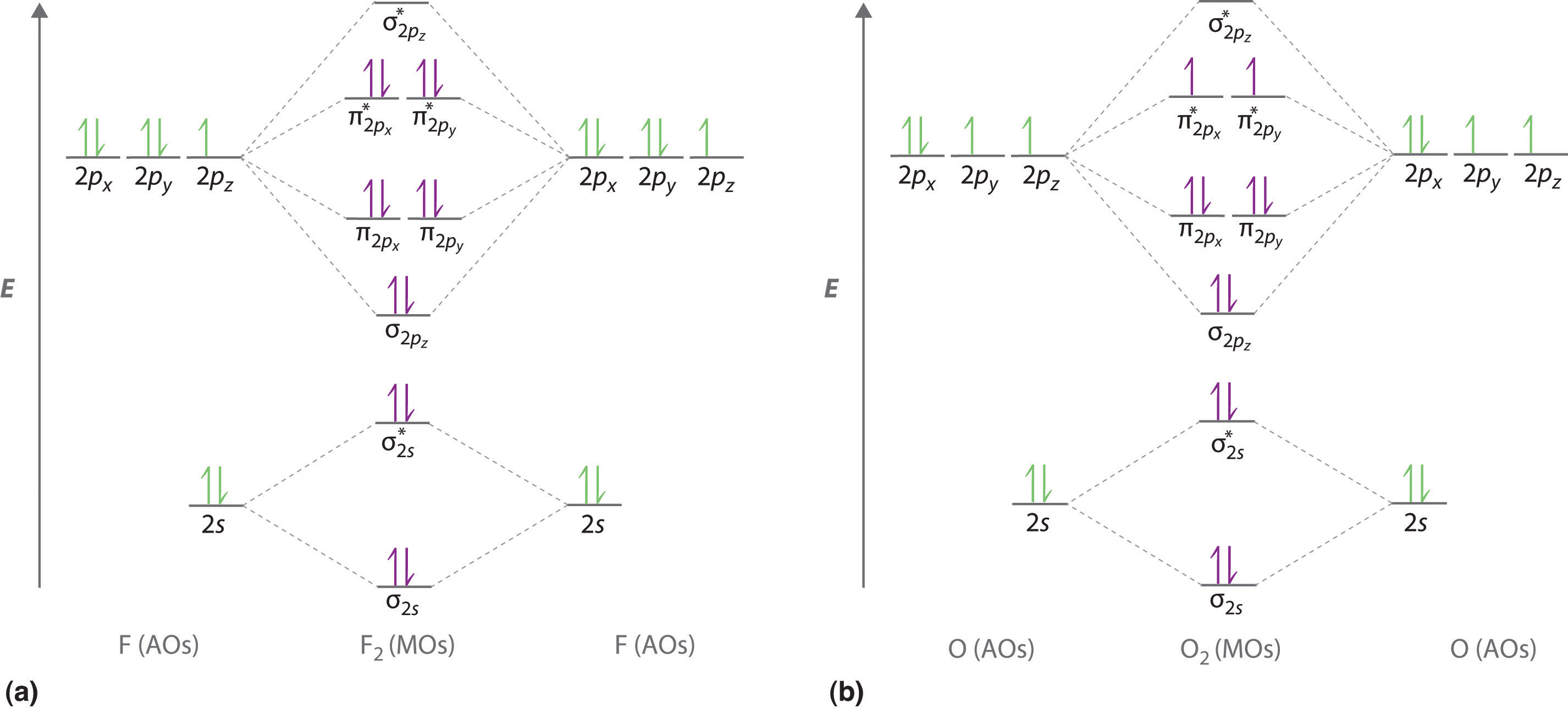
MO Theory of Homonuclear Diatomic Molecules
A sufficient number of orbitals is available for the Aufbau of the ground states of all homonuclear diatomic species from H2 to Ne2. Table 1 summarizes the results. The most likely order in which the molecular orbitals are filled is given by
\[1\sigma_{g}<1\sigma_{u}<2\sigma_{g}<2\sigma_{u}<3\sigma_{g}\sim1\pi_{u}<1\pi_{g}<3\sigma_{u}\]
The relative order of 3\(\sigma_{g}\) and 1\(\pi_{u}\) depends on which other molecular orbitals are occupied, much like the situation involving the 4s and 3d atomic orbitals. The results of photoelectron spectroscopy indicate that 1\(\pi_{u}\) is lower up to and including N2, but 3\(\sigma_{g}\) is lower thereafter.
The term symbol \(\Sigma,\Pi,\Delta\ldots\), analogous to the atomic S, P, D. . . symbolizes the axial component of the total orbital angular momentum. When a \(\pi\)-shell is filled (4 electrons) or half-filled (2 electrons), the orbital angular momentum cancels to zero and we find a \(\Sigma\) term. The spin multiplicity is completely analogous to the atomic case. The total parity is again designated by a subscript g or u. Since the many electron wavefunction is made up of products of individual MO's, the total parity is odd only if the molecule contains an odd number of u orbitals. Thus a \(\sigma_{u}^{2}\) or a \(\pi_{u}^{2}\) subshell transforms like g.
For \(\Sigma\) terms, the superscript \(\pm\) denotes the sign change of the wavefunction under a reflection in a plane containing the internuclear axis. This is equivalent to a sign change in the variable \(\phi\rightarrow-\phi\). This symmetry is needed when we deal with spectroscopic selection rules. In a spin-paired \(\pi_{u}^{2}\) subshell the triplet spin function is symmetric so that the orbital factor must be antisymmetric, of the form
\[\dfrac{1}{\sqrt{2}} \biggl( \pi_{x}(1)\pi_{y}(2)-\pi_{y}(1)\pi_{x}(2) \biggr) \label{6}\]
This will change sign under the reflection, since \(x\rightarrow{x}\) but \(y\rightarrow{-y}\). We need only remember that a \(\pi_{u}^{2}\) subshell will give the term symbol \(^{3}\Sigma_{g}^{-}\).
The net bonding effect of the occupied molecular orbitals is determined by the bond order, half the excess of the number bonding minus the number antibonding. This definition brings the molecular orbital results into correspondence with the Lewis (or valence-bond) concept of single, double and triple bonds. It is also possible in molecular orbital theory to have a bond order of 1/2, for example, in \(H_{2}^{+}\) which is held together by a single bonding orbital. A bond order of zero generally indicates no stable chemical bond, although helium and neon atoms can still form clusters held together by much weaker van der Waals forces. Molecular-orbital theory successfully accounts for the transient stability of a \(^{3}\Sigma_{u}^{+}\) excited state of He2, in which one of the antibonding electrons is promoted to an excited bonding orbital. This species has a lifetime of about 10-4 sec, until it emits a photon and falls back into the unstable ground state. Another successful prediction of molecular orbital theory concerns the relative binding energy of the positive ions N\(_{2}^{+}\) and O\(_{2}^{+}\), compared to the neutral molecules. Ionization weakens the N–N bond since a bonding electron is lost, but it strengthens the O–O bond since an antibonding electron is lost.
One of the earliest triumphs of molecular orbital theory was the prediction that the oxygen molecule is paramagnetic. Figure \(\PageIndex{5}\) shows that liquid O2 is a magnetic substance, attracted to the region between the poles of a permanent magnet. The paramagnetism arises from the half-filled 1\(\pi_{g}^{2}\) subshell. According to Hund's rules the two electrons singly occupy the two degenerate 1\(\pi_{g}\) orbitals with their spins aligned parallel. The term symbol is \(^{3}\Sigma_{g}^{-}\) and the molecule thus has a nonzero spin angular momentum and a net magnetic moment, which is attracted to an external magnetic field. Linus Pauling invented the paramagnetic oxygen analyzer, which is extensively used in medical technology.
Variational Computation of Molecular Orbitals
Thus far we have approached molecular orbital theory from a mainly descriptive point of view. To begin a more quantitative treatment, recall the LCAO approximation to the \(H_{2}^{+}\) ground state, Equation \(\ref{4}\), which can be written
\[\psi=c_{A}\psi_{A}+c_{B}\psi_{B}\label{7}\]
Using this as a trial function in the variational principle, we have
\[E(c_{A},c_{B})=\dfrac{\int\psi\hat{H}\psi{d}\tau}{\int\psi^{2}d\tau}\label{8}\]
where \(\hat{H}\) is the Hamiltonian from Equation \(\ref{1}\). In fact, these equations can be applied more generally to construct any molecular orbital, not just solutions for \(H_{2}^{+}\). In the general case, \(\hat{H}\) will represent an effective one-electron Hamiltonian determined by the molecular environment of a given orbital. The energy expression involves some complicated integrals, but can be simplified somewhat by expressing it in a standard form. Hamiltonian matrix elements are defined by
\[H_{AA}=\int\psi_{A}\hat{H}\psi_{A}d\tau\]\[H_{BB}=\int\psi_{B}\hat{H}\psi_{B}d\tau\]\[H_{AB}=H_{BA}=\int\psi_{A}\hat{H}\psi_{B}d\tau\label{9}\]
while the overlap integral is given by
\[S_{AB}=\int\psi_{A}\psi_{B}d\tau\label{10}\]
Presuming the functions \(\psi_{A}\) and \(\psi_{B}\) to be normalized, the variational energy (Equation \(\ref{8}\)) reduces to
\[E(c_{A}c_{B})=\dfrac{c_{A}^{2}H_{AA}+2c_{A}c_{B}H_{AB}+c_{B}^{2}H_{BB}}{c_{A}^{2}+2c_{A}c_{B}S_{AB}+c_{B}^{2}}\label{11}\]
To optimize the MO, we find the minimum of E wrt variation in cA and cB, as determined by the two conditions
\[\dfrac{\partial{E}}{\partial{c_{A}}}=0,\ \ \ \ \ \dfrac{\partial{E}}{\partial{c_{B}}}=0\label{12}\]
The result is a secular equation determining two values of the energy:
\[\left|\begin{array}{ll}H_{AA}-E&H_{AB}-ES_{AB}\\H_{AB}-ES_{AB}&H_{BB}-E\end{array}\right|=0\label{13}\]
For the case of a homonuclear diatomic molecule, for example \(H_{2}^{+}\), the two Hamiltonian matrix elements \(H_{AA}\) and \(H_{BB}\) are equal, say to \(\alpha\). Setting \(H_{AB}=\beta\) and \(S_{AB}=S\), the secular equation reduces to
\[\left|\begin{array}{ll}\alpha-E&\beta-ES\\\beta-ES&\alpha-E\end{array}\right|=(\alpha-E)^{2}-(\beta-ES)^{2}=0\label{14}\]
with the two roots
\[E^{\pm}=\dfrac{\alpha\pm\beta}{1\pm{S}}\label{15}\]
The calculated integrals \(\alpha\) and \(\beta\) are usually negative, thus for the bonding orbital
\[E^{+}=\dfrac{\alpha+\beta}{1+S}\ \ \ \ \ (bonding)\label{16}\]
while for the antibonding orbital
\[E^{-}=\dfrac{\alpha-\beta}{1-S}\ \ \ \ \ (antibonding)\label{17}\]
Note that \((E^{-}-\alpha)>(\alpha-E^{+})\), thus the energy increase associated with antibonding is slightly greater than the energy decrease for bonding. For historical reasons, \(\alpha\) is called a Coulomb integral and \(\beta\), a resonance integral.
Heteronuclear Molecules
The variational computation leading to Equation \(\ref{13}\) can be applied as well to the heteronuclear case in which the orbitals \(\psi_{A}\) and \(\psi_{B}\) are not equivalent. The matrix elements \(H_{AA}\) and \(H_{BB}\) are approximately equal to the energies of the atomic orbitals \(\psi_{A}\) and \(\psi_{B}\), respectively, say \(E_{A}\) and \(E_{B}\) with \(E_{A}>E_{B}\). It is generally true that \(|E_{A}|,|E_{B}|\gg|H_{AB}|\). With these simplifications, secular equation can be written
\[\left|\begin{array}{ll}E_{A}-E&H_{AB}-ES_{AB}\\H_{AB}-ES_{AB}&E_{B}-E\end{array}\right|=(E_{A}-E)(E_{B}-E)-(H_{AB}-ES_{AB})^{2}=0\label{18}\]
This can be rearranged to \[E-E_{A}=\dfrac{(H_{AB}-ES_{AB})^{2}}{E-E_{B}}\label{19}\]To estimate the root closest to EA, we can replace E by EA on the right hand side of the equation. This leads to\[E^{-}\approx{E_{A}+\dfrac{(H_{AB}-E_{A}S_{AB})^{2}}{E_{A}-E_{B}}}\label{20}\]and analogously for the other root,
\[E^{+}\approx{E_{B}-\dfrac{(H_{AB}-E_{B}S_{AB})^{2}}{E_{A}-E_{B}}}\label{21}\]
The following correlation diagram represents the relative energies of these atomic orbitals and MO's:
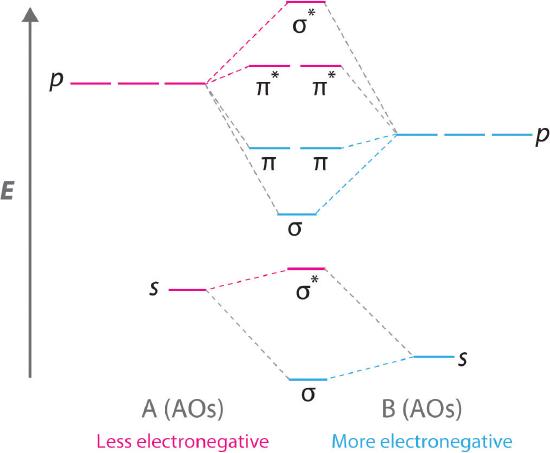
A simple analysis of Equations \(\ref{18}\) implies that, in order for two atomic orbitals \(\psi_{A}\) and \(\psi_{B}\) to form effective molecular orbitals the following conditions must be met:
- (The atomic orbitals must have compatible symmetry. For example, \(\psi_{A}\) and \(\psi_{B}\) can be either s or p\(\sigma\) orbitals to form a \(\sigma\)-bond or both can be p\(\pi\) (with the same orientation) to form a \(\pi\)-bond.
- The charge clouds of \(\psi_{A}\) and \(\psi_{B}\) should overlap as much as possible. This was the rationale for hybridizing the s and p orbitals in carbon. A larger value of SAB implies a larger value for HAB.
- The energies EA and EB must be of comparable magnitude. Otherwise, the denominator in (20) and (21) will be too large and the molecular orbitals will not differ significantly from the original AO's. A rough criterion is that EA and EB should be within about 0.2 hartree or 5 eV. For example, the chlorine 3p orbital has an energy of -13.0 eV, comfortably within range of the hydrogen 1s, with energy -13.6 eV. Thus these can interact to form a strong bonding (plus an antibonding) molecular orbital in HCl. The chlorine 3s has an energy of -24.5 eV, thus it could not form an effective bond with hydrogen even if it were available.
Hückel Molecular Orbital Theory
Molecular orbital theory has been very successfully applied to large conjugated systems, especially those containing chains of carbon atoms with alternating single and double bonds. An approximation introduced by Hückel in 1931 considers only the delocalized p electrons moving in a framework of \(\sigma\)-bonds. This is, in fact, a more sophisticated version of a free-electron model. We again illustrate the model using butadiene CH2=CH-CH=CH2. From four p atomic orbitals with nodes in the plane of the carbon skeleton, one can construct four \(\pi\) molecular orbitals by an extension of the LCAO approach:
\[\psi=c_{1}\psi_{1}+c_{2}\psi_{2}+c_{3}\psi_{3}+c_{4}\psi_{4}\label{22}\]
Applying the linear variational method, the energies of the molecular orbitals are the roots of the 4 x 4 secular equation
\[\left|\begin{array}{lcc}H_{11}-E&H_{12}-ES_{12}&\ldots\ \ \ \\H_{12}-ES_{12}&H_{22}-E&\ldots\ \ \ \\\ \ \ \ \ \ \ \ldots&\ldots&\ldots\ \ \ \end{array}\right|=0\label{23}\]
Four simplifying assumptions are now made
- All overlap integrals Sij are set equal to zero. This is quite reasonable since the p-orbitals are directed perpendicular to the direction of their bonds.
- All resonance integrals Hij between non-neighboring atoms are set equal to zero.
- All resonance integrals Hij between neighboring atoms are set equal to \(\beta\).
- All coulomb integrals Hii are set equal to \(\alpha\).
The secular equation thus reduces to
\[\left|\begin{array}{cccc}\alpha-E&\beta&0&0\\\beta&\alpha-E&\beta&0\\0&\beta&\alpha-E&\beta\\0&0&\beta&\alpha-E\end{array}\right|=0\label{24}\]
Dividing by \(\beta^{4}\) and defining
\[x=\dfrac{\alpha-E}{\beta}\label{25}\]
the equation simplifies further to
\[\left|\begin{array}{cccc}x&1&0&0\\1&x&1&0\\0&1&x&1\\0&0&1&x\end{array}\right|=0\label{26}\]
This is essentially the connection matrix for the molecule. Each pair of connected atoms is represented by 1, each non-connected pair by 0 and each diagonal element by \(x\). Expansion of the determinant gives the 4th order polynomial equation
\[x^{4}-3x^{2}+1=0\label{27}\]
Noting that this is a quadratic equation in \(x^{2}\), the roots are found to be \(x^{2}=(3\pm\sqrt{5})/2\), so that \(x=\pm0.618,\pm1.618\). This corresponds to the four MO energy levels
\[E=\alpha\pm1.618\beta,\ \ \ \ \ \alpha\pm0.618\beta\label{28}\]
Since \(\alpha\) and \(\beta\) are negative, the lowest molecular orbitals have
\[E(1\pi)=\alpha+1.618\beta\]
and
\[E(2\pi)=\alpha+0.618\beta\]
and the total \(\pi\)-electron energy of the \(1\pi^{2}2\pi^{2}\) configuration equals
\[E_{\pi}=2(\alpha+1.618\beta)+2(\alpha+0.618\beta)=4\alpha+4.472\beta\label{29}\]
The simplest application of Hückel theory, to the ethylene molecule CH2=CH2 gives the secular equation
\[\left|\begin{array}{cc}x&1\\1&x\end{array}\right|=0\label{30}\]
This is easily solved for the energies \(E=\alpha\pm\beta\). The lowest orbital has \(E(1\pi)=\alpha+\beta\) and the 1\(\pi^{2}\) ground state has \(E_{\pi}=2(\alpha+\beta)\). If butadiene had two localized double bonds, as in its dominant valence-bond structure, its \(\pi\)-electron energy would be given by \(E_{\pi}=4(\alpha+\beta)\). Comparing this with the Hückel result (Equation \(\ref{29}\)), we see that the energy lies lower than the that of two double bonds by \(0.48\beta\). The thermochemical value is approximately -17 kJmol-1. This stabilization of a conjugated system is known as the delocalization energy. It corresponds to the resonance-stabilization energy in valence-bond theory.
Aromatic systems provide the most significant applications of Hückel theory. For benzene, we find the secular equation
\[\left|\begin{array}{cccccc}x&1&0&0&0&1\\1&x&1&0&0&0\\0&1&x&1&0&0\\0&0&1&x&1&0\\0&0&0&1&x&1\\1&0&0&0&1&x\end{array}\right|=0\label{31}\]
with the six roots \(x=\pm2,\pm1,\pm1\). The energy levels are \(E=\alpha\pm2\beta\) and two-fold degenerate \(E=\alpha\pm\beta\). With the three lowest molecular orbitals occupied, we have
\[E_{\pi}=2(\alpha+2\beta)+4(\alpha+\beta)=6\alpha+8\beta\label{32}\]
Since the energy of three localized double bonds is \(6\alpha+6\beta\), the delocalization energy equals \(2\beta\). The thermochemical value is -152 kJmol-1.
Contributors
Seymour Blinder (Professor Emeritus of Chemistry and Physics at the University of Michigan, Ann Arbor)

