10: The Chemical Bond
- Page ID
- 8859
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Hydrogen Molecule
This four-particle system, two nuclei plus two electrons, is described by the Hamiltonian
\[ \hat{H} = -\frac{1}{2} \nabla^2_1 -\frac{1}{2} \nabla^2_2 -\frac{1}{2M_A} \nabla^2_A -\frac{1}{2M_B} \nabla^2_B -\frac{1}{r_{1A}} -\frac{1}{r_{2B}} -\frac{1}{r_{2A}} -\frac{1}{r_{1B}} +\frac{1}{r_{12}} +\frac{1}{R} \label{1}\]
in terms of the coordinates shown in Figure \(\PageIndex{1}\). We note first that

the masses of the nuclei are much greater than those of the electrons,Mproton = 1836 atomic units, compared to melectron = 1 atomic unit. Therefore nuclear kinetic energies will be negligibly small compared to those of the electrons. In accordance with the Born-Oppenheimer approximation, we can first consider the electronic Schrödinger equation
\[\hat{H}_{elec} \psi(r_1,r_2,R) = E_{elec}(R) \psi(r_1,r_2,R) \label{2}\]
where
\[ \hat{H} = -\frac{1}{2} \nabla^2_1 -\frac{1}{2} \nabla^2_2 -\frac{1}{r_{1A}} -\frac{1}{r_{2B}} -\frac{1}{r_{2A}} -\frac{1}{r_{1B}} +\frac{1}{r_{12}} +\frac{1}{R} \label{3}\]
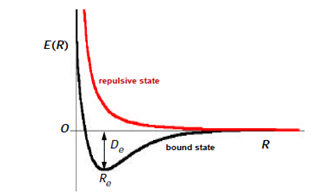
The internuclear separation R occurs as a parameter in this equation so that the Schrödinger equation must, in concept, be solved for each value of the internuclear distance R. A typical result for the energy of a diatomic molecule as a function of R is shown in Figure \(\PageIndex{2}\). For a bound state, the energy minimum occurs at for R = Re, known as the equilibrium internuclear distance. The depth of the potential well at Re is called the binding energy or dissociation energy De. For the H2 molecule, De = 4.746 eV and Re=1.400 bohr = 0.7406 Å. Note that as R → 0, E(R) → \(\infty\), since the 1/R nuclear repulsion will become dominant.
The more massive nuclei move much more slowly than the electrons. From the viewpoint of the nuclei, the electrons adjust almost instantaneously to any changes in the internuclear distance. The electronic energy Eelec(R) therefore plays the role of a potential energy in the Schrödinger equation for nuclear motion
\[ \left\{ -\frac{1}{2M_A} \nabla^2_A -\frac{1}{2M_B} \nabla^2_B + V(R)\right\} \chi (r_A,r_B) = E \chi (r_A,r_B) \label{4}\]
where
\[ V(R) = E_{elec}(R) \label{5}\]
from solution of Equation \(\ref{2}\). Solutions of Equation \(\ref{4}\) determine the vibrational and rotational energies of the molecule. These will be considered elsewhere. For the present, we are interested in the obtaining electronic energy from Equation \(\ref{2}\) and \(\ref{3}\). We will thus drop the subscript "elec" on \(\hat{H}\) and E(R) for the remainder this Chapter.
The first quantum-mechanical account of chemical bonding is due to Heitler and London in 1927, only one year after the Schrödinger equation was proposed. They reasoned that, since the hydrogen molecule H2 was formed from a combination of hydrogen atoms A and B, a first approximation to its electronic wavefunction might be
\[ \psi(r_1,r_2) = \psi_{1s} (r_{1A})\psi_{1s} (r_{2B}) \label{6}\]
Using this function into the variational integral
\[ \tilde{E}(R) = \frac{\int{ \psi \hat{H} \psi d\tau}}{\int{\psi^2 d\tau}} \label{7}\]
the value Re \(\approx\) 1.7 bohr was obtained, indicating that the hydrogen atoms can indeed form a molecule. However, the calculated binding energy De \(\approx\) 0.25 eV, is much too small to account for the strongly-bound H2 molecule. Heitler and London proposed that it was necessary to take into account the exchange of electrons, in which the electron labels in Equation \(\ref{6}\) are reversed. The properly symmetrized function
\[ \psi(r_1, r_2) = \psi_{1s} (r_{1A})\psi_{1s} (r_{2B}) +\psi_{1s} (r_{1B})\psi_{1s} (r_{2A}) \label{8}\]
gave a much more realistic binding energy value of 3.20 eV, with Re = 1.51 bohr. We have already used exchange symmetry (and antisymmetry) in our treatment of the excited states of helium. The variational function (Equation \(\ref{8}\)) was improved (Wang, 1928) by replacing the hydrogen 1s functions \(e^{-r}\) by \(e^{-\zeta r}\). The optimized value \(\zeta\) = 1.166 gave a binding energy of 3.782 eV. The quantitative breakthrough was the computation of James and Coolidge (1933). Using a 13-parameter function of the form
\[ \psi(r_1, r_2) = e^{- \alpha ( \xi_{1}+\xi_{2})} \mbox{ x polynomial in} \{ \xi_{1}, \xi_{2}, \eta_{1}, \eta_{2}, \rho \} , \xi_{i} \equiv \frac{r_{iA} + r_{iB}}{R}, \eta_{i} \equiv \frac{r_{iA}+r_{iB}}{R}, \rho \equiv \frac{r_{12}}{R} \label{9}\]
they obtained Re = 1.40 bohr, De = 4.720 eV. In a sense, this result provided a proof of the validity of quantum mechanics for molecules, in the same sense that Hylleraas' computation on helium was a proof for many-electron atoms.
The Valence Bond Theory
The basic idea of the Heitler-London model for the hydrogen molecule can be extended to chemical bonds between any two atoms. The orbital function (8) must be associated with the singlet spin function \(\sigma_{0,0}(1,2)\) in order that the overall wavefunction be antisymmetric. This is a quantum-mechanical realization of the concept of an electron-pair bond, first proposed by G. N. Lewis in 1916. It is also now explained why the electron spins must be paired, i.e., antiparallel. It is also permissible to combine an antisymmetric orbital function with a triplet spin function but this will, in most cases, give a repulsive state, as shown by the red curve in Figure \(\PageIndex{2}\).
According to valence-bond theory, unpaired orbitals in the valence shells of two adjoining atoms can combine to form a chemical bond if they overlap significantly and are symmetry compatible. A \(\sigma\)-bond is cylindrically symmetrical about the axis joining the atoms. Two s AO's, two pz AO's or an s and a pz can contribute to a \(\sigma\)-bond, as shown in Figure \(\PageIndex{3}\). The z-axis is chosen along the internuclear axis. Two px or two py AO's can form a \(\pi\)-bond, which has a nodal plane containing the internuclear axis. Examples of symmetry-incompatible AO's would be an s with a px or a px with a py. In such cases the overlap integral would vanish because of cancelation of positive and negative contributions. Some possible combinations of AO's forming \(\sigma\) and \(\pi\) bonds are shown in Figure \(\PageIndex{3}\).
Bonding in the HCl molecule can be attributed to a combination of a hydrogen 1s with an unpaired 3pz on chlorine. In Cl2, a sigma bond is formed between the 3pz AO's on each chlorine. As a first approximation, the other doubly-occupied AO's on chlorine-the inner shells and the valence-shell lone pairs-are left undisturbed.
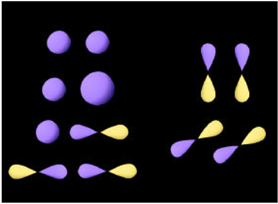
The oxygen atom has two unpaired 2p-electrons, say 2px and 2py. Each of these can form a \(\sigma\)-bond with a hydrogen 1s to make a water molecule. It would appear from the geometry of the p-orbitals that the HOH bond angle would be 90°. It is actually around 104.5°. We will resolve this discrepency shortly. The nitrogen atom, with three unpaired 2p electrons can form three bonds. In NH3, each 2p-orbital forms a \(\sigma\)-bond with a hydrogen 1s. Again 90° HNH bond angles are predicted, compared with the experimental 107°. The diatomic nitrogen molecule has a triple bond between the two atoms, one \(\sigma\) bond from combining 2pz AO's and two \(\pi\) bonds from the combinations of 2px's and 2py's, respectively.
Hybrid Orbitals and Molecular Geometry
To understand the bonding of carbon atoms, we must introduce additional elaborations of valence-bond theory. We can write the valence shell configuration of carbon atom as 2s22px2py, signifying that two of the 2p orbitals are unpaired. It might appear that carbon would be divalent, and indeed the species CH2 (carbene or methylene radical) does have a transient existence. But the chemistry of carbon is dominated by tetravalence. Evidently it is a good investment for the atom to promote one of the 2s electrons to the unoccupied 2pz orbital. The gain in stability attained by formation of four bonds more than compensates for the small excitation energy. It can thus be understood why the methane molecule CH4 exists. The molecule has the shape of a regular tetrahedron, which is the result of hybridization, mixing of the s and three p orbitals to form four sp3 hybrid atomic orbitals. Hybrid orbitals can overlap more strongly with neighboring atoms, thus producing stronger bonds. The result is four C-H \(\sigma\)-bonds, identical except for orientation in space, with 109.5° H-C-H bond angles.
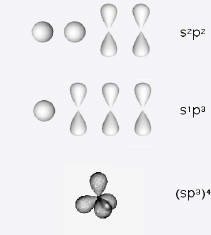
Other carbon compounds make use of two alternative hybridization schemes. The s AO can form hybrids with two of the p AO's to give three sp2 hybrid orbitals, with one p-orbital remaining unhybridized. This accounts for the structure of ethylene (ethene):
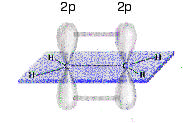
The C-H and C-C \(\sigma\)-bonds are all trigonal sp2 hybrids, with 120° bond angles. The two unhybridized p-orbitals form a \(\pi\)-bond, which gives the molecule its rigid planar structure. The two carbon atoms are connected by a double bond, consisting of one \(\sigma\) and one \(\pi\). The third canonical form of sp-hybridization occurs in C-C triple bonds, for example, acetylene (ethyne). Here, two of the p AO's in carbon remain unhybridized and can form two \(\pi\)-bonds, in addition to a \(\sigma\)-bond, with a neighboring carbon:
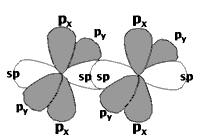
Acetylene H-C\(\equiv\)C-H is a linear molecule since sp-hybrids are oriented 180° apart.
The deviations of the bond angles in H2O and NH3 from 90° can be attributed to fractional hybridization. The angle H-O-H in water is 104.5° while H-N-H in ammonia is 107°. It is rationalized that the p-orbitals of the central atom acquire some s-character and increase their angles towards the tetrahedral value of 109.5°. Correspondingly, the lone pair orbitals must also become hybrids. Apparently, for both water and ammonia, a model based on tetrahedral orbitals on the central atoms would be closer to the actual behavior than the original selection of s- and p-orbitals. The hybridization is driven by repulsions between the electron densities of neighboring bonds.
Valence Shell Model
An elementary, but quite successful, model for determining the shapes of molecules is the valence shell electron repulsion theory (VSEPR), first proposed by Sidgewick and Powell and popularized by Gillespie. The local arrangement of atoms around each multivalent center in the molecule can be represented by AXn-kEk, where X is another atom and E is a lone pair of electrons. The geometry around the central atom is then determined by the arrangement of the n electron pairs (bonding plus nonbonding), which minimizes their mutual repulsion. The following geometric configurations satisfy this condition:
n shape
2 linear 5 trigonal bipyramid
3 trigonal planar 6 octahedral
4 tetrahedral 7 pentagonal bipyramid
The basic geometry will be distorted if the n surrounding pairs are not identical. The relative strength of repulsion between pairs follows the order E-E > E-X > X-X. In ammonia, for example, which is NH3E, the shape will be tetrahedral to a first approximation. But the lone pair E will repel the N-H bonds more than they repel one another. Thus the E-N-H angle will increase from the tetrahedral value of 109.5°, causing the H-N-H angles to decrease slightly. The observed value of 107° is quite well accounted for. In water, OH2E2, the opening of the E-O-E angle will likewise cause a closing of H-O-H, and again, 104.5° seems like a reasonable value.
Valence-bond theory is about 90% successful in explaining much of the descriptive chemistry of ground states. VB theory fails to account for the triplet ground state of O2 or for the bonding in electron-deffcient molecules such as diborane, B2H6. It is not very useful in consideration of excited states, hence for spectroscopy. Many of these deficiencies are remedied by molecular orbital theory, which we take up in the next Chapter.


