Wave-Particle Duality
- Page ID
- 1656
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Quantum mechanics incorporates the idea of wave mechanics that demonstrates the idea of wave-particle duality.This notion suggests that matter can display simultaneously both particle and wave-like properties. This new approach came from Louis de Broglie who built upon Einstein's conception that light possessed particle-like properties in his attempt to explain the photoelectric effect.
Photoelectric Effect
Albert Einstein showed that the dependence on frequency could not be justified by the classical wave theory alone, so he provided a particle perspective. In 1905 he declared that photons (named by G.N. Lewis), were "particles of light" that had similar energy to that of Planck's equation. This equation states that the frequency and energy of a quantum of electromagnetic radiation are proportional. Einstein's idea was revolutionary because he brought a new perspective at looking at light not only as a wave, but as a particle.
Planck's equation: E=hv Planck's constant: h=6.626x10-34 Js 
The photoelectric effect phenomenon that electrons are emitted when light strikes the surface of metals was discovered by Heinrich Hertz in 1888. This process holds true when the incident light has a higher frequency than a certain threshold value. The amount of electrons ejected is determined by the intensity of the incident light, however, the frequency of the light effects the kinetic energies of the emitted electrons.
In other words, the intensity can be described as the brightness from a source of light. So by increasing brightness, intensity increases, and so does energy released. The energy output will be greater and when this happens the amplitude of the light wave increases. But it doesn't matter how much energy is increased or how much you increase the amplitude when it comes to trying to emit electrons from a metallic surface. To do so, frequency must increase.
Increase brightness (maintains frequency and energy)-->Increases Intensity (increases#of phot ons)-->Increases # of electrons emitted
ons)-->Increases # of electrons emitted
Increase frequency-->Increases kinetic energy of electrons
Einstein explanation was that light had the characteristic of a particle (photon) with the photon energy of E=hv. He concluded that if the threshold frequency of the metal was greater than the frequency of the photon, then the photon will have no effect when it bombards the metal surface. However, if the photon reached the threshold frequency it could cause one electron to be emitted. In order to emit more electrons, the light source must be brightened to increase intensity, which still maintains frequency of light and same energy, but increases the number of photons.
Threshold frequency: Vo= (eVo)/h = work function/Planck's constant
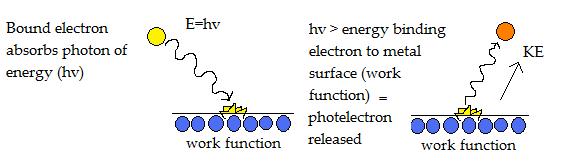
The photoelectric effect can occur even with the lowest frequency light called the threshold frequency.
Photelectrons are released when photon energy (hv) is greater than the work function. Energy in excess is released as kinetic energy in the ejected photoelectron and is proportional to frequency of light.
The diagram above illustrates an electron being striked by a photon of energy, which allows it to overcome the work function binding it to the metal surface. As a result, a photoelectron is emitted with kinetic energy.
By applying the law of conservation of energy we get the equation: hv =eVo+(1/2)mv2
To summarize, regardless of the intensity of light, no electrons will be emitted if the frequency of light is below the threshold frequency (Vo) of the metal surface.

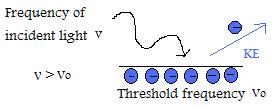
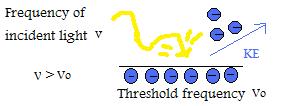
- If the frequency of incident light is above the threshold frequency,then kinetic energy of the emitted particle will increase linearly in respect to the magnitude of frequency.
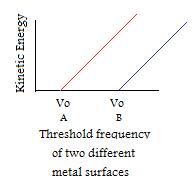
- If incident light frequency is greater than threshold frequency, the number of emitted electrons is determined by intensity. (IMPORTANT NOTE: Kinetic energy per electron doesn't change if intensity is changed, only when frequency is manipulated)
- Although each metal has it's own unique threshold frequency, they all have similar patterns.
De Broglie Wavelength
In 1924, Louis de Broglie used Einstein's equation E=mc2 and incorporated it with Planck's equation. This brought together the relationship of the mass of a photon and speed of light with the photon energy.
Einstein's equation: E=mc2 m=mass of photon c=speed of light COMBINED WITH Planck's equation: E=hv
E=mc2 & E=hv --> mc2=hv --> mc=(hv)/c=p where p is momentum
Since wavelegth is speed of light/frequency as shown by λ=c/f momentum is equivalent to p=(hv)/c=h/λ
In order for this equation to apply for the purpose of a material particle (electron), de Broglie changed the equation to its equivalent
So p=h/λ changed to λ=h/p=h/(mv) where p is the product of mass of particle and velocity
λ=h/(mv) demonstrates that particles have wavelike properties as shown by the integration of wavength (λ), Planck's constant (h), and momentum of particle (p=mv). This equation is also known as the "de Broglie wavelength." He reasoned that if things that acted like waves had particle characteristics then it should work vice versa. Therefore, things that behave like particles should also have wave characteristics. He coined the term "matter waves" to describe waves that involved material particles, such as electrons.
Particle Properties
Single Slit Diffraction

Pattern is made up of emitted particles
Double Slit Diffraction

Pattern is similar to wave interference
Wave Properties
When waves travel in the same medium, interference can occur. Interference is the net effect caused by two different waves. In the example below, the superposition principle is in effect. The diagram shows that when two waves are traveling with the same frequency through the same medium, the individual waves pass one another without disturbance.
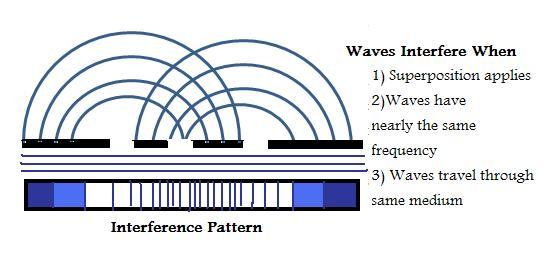  |
There are two types of interferences known as Constructive and Destructive Interference.
1. Constructive Interference - When waves are "in phase" this means that their crests and troughs coincide. The net result produces a combination of the two waves that produces high crests and deep troughs causing amplification. The waves overlap and create an even larger wave.
2. Destructive Interference - This occurs when waves cancel one another because the crest of one wave occurs at the trough of another and is considered "out of phase."
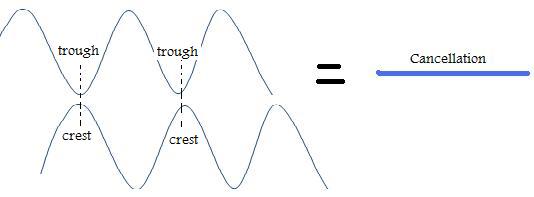
Uncertainty Principle
The wave-particle duality limits our understanding in determining the position and momentum of subatomic particles. In the 1920's, Werner Heisenberg and Niels Bohr tried different experiments to precisely measure the behavior of particles. However, they were unable to simultaneously measure position and momentum at the same time. This meant that even if they knew where a particle was, they couldn't find where it was going nor where it came from, after all the wave is spread out. They concluded that it was impossible to accurately measure and determine an electron's momentum and position simultaneously, hence the uncertainty principle is also referred to as the principle of indeterminacy.
Examples
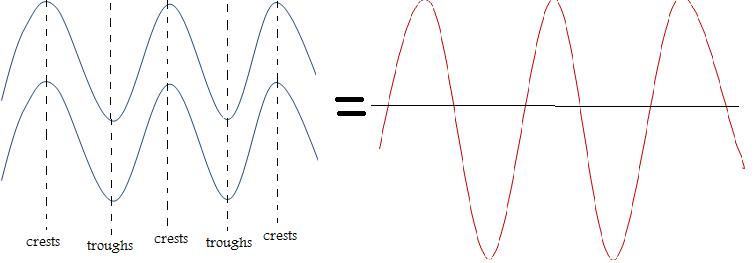
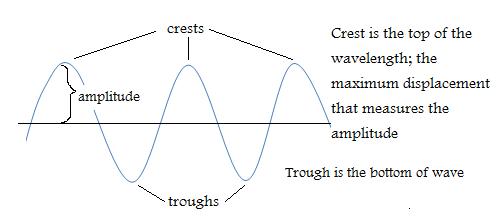
1. From this diagram determine the number of crests and troughs. Remember crests are the high peaks and troughs form the deep ends. Therefore, there are 4 crests and 3 troughs.
2. If a radiation has a wavelength of 302.5nm, what is the energy of one photon?
To do this, we must look at Planck's equation and find the frequency of the radiation.
Frequency is v= c/λ and c=speed of light (2.998x108 m/s) --> v= (2.998x108 m/s)/302.5x10-9m = 9.911x1014s-1
Planck's equation E=hv = (6.626x10-34Js/photon)(9.911x1014s-1)=6.567x10-19J/photon
3. A photon has a frequency of 5.5x103Hz. Convert this to wavelength.
c=λv so λ=c/v= (2.998x108 m/s)/5.5x103Hz=5.5x104m Remember Hz is equivalent to s-1
5.5x104m (1nm/10-9m)= 5.5x1013nm Remember wavelengths are expressed in nanometers (nm)
4. What is the de Broglie wavelength of a 1.5g bouncy ball traveling at 20m/s?
λ=h/mv Convert g to kg so 1.5g(1kg/103g)=,0015kg Joule=Nm Newton=kgm/s2
λ=h/mv = 6.626x10-34Js/(.0015kgx20m/s)=2.209x10-32m Stoichiometry=Js/[kg(m/s)]=(Ns2/kg)=(kgms2/kgs2)=m
2.209x10-32m (1nm/10-9m)= 2.2x10-23nm
5. If a metal had a threshold frequency of 7.38x1013Hz, would it display the photelectric effect with infrared light?
The maximum frequency of infrared light is about 3x1014Hz. Since this is above the threshold frequency for the metal, it will display the photoelectric effect. However, if the threshold frequency was greater than the infrared light frequency, no photoelectric effect would occur.
Problems
1. How many crests and troughs are shown here?
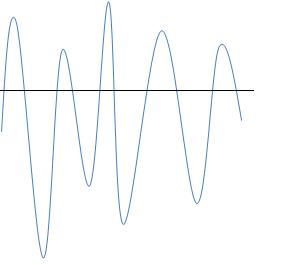
2. The higher the frequency, the __________(smaller/greater) the wavelength.
3. Intensity of the incident light effects the amount of ______ emitted, whereas the frequency of incident light effects the _____ energy.
4. Using Planck's equation determine the frequency of radiation if it has an energy of 3.21x10-28 J/photon.
5. What is the energy (in joules) of a photon with a threshold frequency radiation of 8.67X1012Hz?
6. What is the de Broglie wavelenth of a 8.5g tennis bal traveling at 12.6m/s?
Inside Links
Outside Links
- Interference (Wave Propogation)
- Double-Slit Experiment
References
- Petrucci, Ralph H., William S. Harwood, F. Geoffrey Herring, & Jeffry D. Madura. General Chemistry: Principles and Modern Applications. 9th ed. Upper Saddle River, New Jersey, 1993.
- Achinstein, Peter. Particles And Waves: Historical Essays In The Philosophy Of Science. New York: Oxford UP, 1991.
- Bruno, Leonard C. Science And Technology Breakthroughs: From The Wheel To The World Wide Web. Vol. 2. United States: UXL An Imprint of Gale,1998.
Contributors and Attributions
- Maryann Hernandez (UCD)