Particle in a 2-Dimensional Box
- Page ID
- 1725
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Manipulate probability, energy, and transition problems involving multidimensional wavefunctions
- Apply the Separation of Variables to solve a multi-dimensional Schrödinger equation
- Manipulate problems with multiple quantum numbers
- To be introduced to the concepts of non-singular nodes (e.g., nodal lines)
- To be introduced to the concept of degeneracy
Let us now consider the Schrödinger Equation for an electron confined to a two dimensional box, \(0 < x < a\) and \(0 < y < b\). That is to say, within this rectangle the electron wavefunction behaves as a free particle (\(V(x,y) = 0\)), but the walls are impenetrable so the wavefunction \(\psi(x,y,t)=0\) at the walls.
Extending the (time-independent) Schrödinger equation for a one-dimensional system
\[−\frac{\hbar^2}{2m}\frac{d^ 2\psi(x)}{d x^2}+V(x)\psi(x)=E\psi(x) \label{3.1.3}\]
to a two-dimensional system is not difficult
\[- \dfrac{\hbar^2}{2m} \left (\dfrac{\partial^2 \psi(x,y)}{\partial x^2} + \dfrac{\partial ^2 \psi(x,y)}{\partial y^2} \right) + V(x,y)\psi(x,y) = E \psi(x,y). \label{e1}\]
Equation \ref{e1} can be simplified for the particle in a 2D box since we know that \(V(x,y) =0\) within the box and \(V(x,y) = \infty\) outside the box, ii.e.
\[V(x,y)=\begin{cases}
0 & 0\leq x\leq a \; \text{and}\; 0\leq y\leq b\\
\infty & x< 0 \; \text{and}\; x> a \\
\infty & y< 0 \; \text{and}\; y> b \end{cases}\nonumber\]
So Equation \ref{e1} becomes
\[- \dfrac{\hbar^2}{2m} \left (\dfrac{\partial^2 \psi(x,y)}{\partial x^2} + \dfrac{\partial ^2 \psi(x,y)}{\partial y^2} \right) = E \psi(x,y). \label{e2}\]
Since the Hamiltonian (i.e. left side of Equation \ref{e2}) is the sum of two terms with independent (separate) variables, we try a product wavefunction like in the Separation of Variables approach used to separate time-dependence from the spatial dependence previously. Within this approach we express the 2-D wavefunction as a product of two independent 1-D components
\[\psi(x,y) = X(x)Y(y). \label{product}\]
This ansatz separates Equation \ref{e2} into two independent one-dimensional Schrödinger equations
\[- \dfrac{\hbar^2}{2m} \left (\dfrac{d^2 X(x)}{d x^2} \right) = \varepsilon_x X(x). \label{e3a}\]
\[- \dfrac{\hbar^2}{2m} \left (\dfrac{d ^2 Y(y)}{d y^2} \right) = \varepsilon_y Y(y). \label{e3b}\]
where the total energy of the particle is the sum of the energies from each one-dimensional Schrödinger equation
\[E=\varepsilon_x +\varepsilon_y \label{sum}\]
The differential equations in Equations \ref{e3a} and \ref{e3b} are familiar as they were found for the particle in a 1-D box previously. They have the general solution
\[ X(x) = A_x \sin (k_x x) + B_x \cos(k_xx) \label{e4a}\]
\[ Y(y) = A_y \sin (k_y y) + B_y \cos(k_y y) \label{e4b}\]
Applying Boundary Conditions
The general solutions in Equations \ref{e4a} and \ref{e4b} can be simplified to address boundary conditions dictated by the potential, i.e., \(\psi(0,y)=0\) and \(\psi(x,0)=0\). Therefore, \(B_x=0\) and \(B_y=0\).
Thus, we can combine Equations \ref{e4a}, \ref{e4b}, and \ref{product} to construct the wavefunction \(\psi (x,y)\) for a particle in a 2D box of the form
\[\psi (x,y)=N \sin\left ( \sqrt{\dfrac{2m\varepsilon_x}{\hbar^2}}x \right ) \sin \left ( \sqrt{\dfrac{2m\varepsilon_y}{\hbar^2}}y \right ) \label{wave}\]
We still need to satisfy the remaining boundary conditions \(\psi (L,y)=0\) and \(\psi (x,L)=0\)
\[N \sin\left ( \sqrt{\dfrac{2m\varepsilon_x}{\hbar^2}}L \right ) \sin \left ( \sqrt{\dfrac{2m\varepsilon_y}{\hbar^2}}y \right ) = 0 \label{cond1}\]
and
\[N\sin\left ( \sqrt{\dfrac{2m\varepsilon_x}{\hbar^2}}x \right ) \sin \left ( \sqrt{\dfrac{2m\varepsilon_y}{\hbar^2}}L \right ) = 0 \label{cond2}\]
Equation \ref{cond1} can be satisfied if
\[\sin\left ( \sqrt{\dfrac{2m\varepsilon_x}{\hbar^2}}L \right ) =0\]
independent of the value of \(y\), while Equation \ref{cond2} can be satisfied if
\[\sin\left ( \sqrt{\dfrac{2m\varepsilon_y}{\hbar^2}}L \right ) =0\]
independent of the value of \(x\). These are the same conditions that we encountered for the one-dimensional box, hence we already know the \(\sin\) function in each case can be zero in many places. In fact, these two conditions are satisfied if
\[\sqrt{\dfrac{2m\varepsilon_x}{\hbar^2}}L = n_x \pi\]
and
\[ \sqrt{\dfrac{2m\varepsilon_y}{\hbar^2}}L = n_y \pi \]
which yield the allowed values of \(\varepsilon_x\) and \(\varepsilon_y\) as
\[\varepsilon_{n_x}=\dfrac{\hbar^2 \pi^2}{2mL^2}n_{x}^{2}\]
and
\[ \varepsilon_{n_y}=\dfrac{\hbar^2 \pi^2}{2mL^2}n_{y}^{2}\]
We need two different integers \(n_x\) and \(n_y\) because the conditions are completely independent and can be satisfied by any two different (or similar) values of these integers. The allowed values of the total energy are now given by
\[E_{n_x, n_y}=\dfrac{\hbar^2 \pi^2}{2mL^2}(n_{x}^{2}+n_{y}^{2}) \label{squareE}\]
Note that the allowed energies now depend on two integers \(n_x\) and \(n_y\) rather than one. These arise from the two independent boundary conditions in the \(x\) and \(y\) directions. As in the one-dimensional box, the values of \(n_x\) and \(n_y\) are both restricted to the natural numbers \(1,2,3,...\) Note, therefore, that the ground state energy \(E_{1,1}\) is
\[E_{1,1}=\dfrac{\hbar^2 \pi^2}{mL^2}\]
is larger than for the one-dimensional box because of the contributions from kinetic energy in the \(x\) and \(y\) directions.
Once the conditions on \(\varepsilon_{n_x}\) and \(\varepsilon_{n_y}\) are substituted into Equation \ref{wave}, the wavefunctions become
\[\psi_{n_x, n_y}(x,y)=N\sin\left ( \dfrac{n_x \pi x}{L} \right ) \sin \left ( \dfrac{n_y \pi y}{L} \right )\]
The constant \(N\) is now determined by the normalization condition
\[\begin{align*}\int_{0}^{L} \int_{0}^{L}|\psi_{n_x, n_y}(x,y)|^2 dx\,dy &= 1\\ N^2 \int_{0}^{L}\sin^2\left ( \dfrac{n_x \pi x}{L} \right ) dx\int_{0}^{L}\sin^2 \left ( \dfrac{n_y \pi y}{L} \right )dy &= 1\\ N^2\dfrac{L}{2}\cdot \dfrac{L}{2} &= 1\\ N &= \dfrac{2}{L}\end{align*}\]
so that the complete normalized 2D wavefunction is
\[\psi_{n_x, n_y}(x,y)=\dfrac{2}{L}\sin\left ( \dfrac{n_x \pi x}{L} \right ) \sin\left ( \dfrac{n_y \pi y}{L} \right ) \label{squareWF}\]
Because the Halmiltonian in Equation \ref{e2} can be expressed as a simple sum of independent terms, the solutions can be expressed as simple products of the one-dimensional solution (Equation \ref{squareWF}) with energies that are expressed as the sum of one-dimensional energies (Equation \ref{squareE}). This observation extends to higher dimensional wavefunctions as demonstrated later.
The wavefunctions in Equation \ref{squareWF} are somewhat more difficult that 1-D analogs to visualize because they are two dimensional. Nevertheless, we can still visualize them, and Figure \(\PageIndex{1}\) shows the following wavefunctions: \(\psi_{1,1}(x,y)\), \(\psi_{2,1}(x,y)\) and \(\psi_{2,2}(x,y)\).
Figure \(\PageIndex{1}\): Visualizing the first six wavefunctions for a particle in a two-dimensional square box (\(L_x=L_y=L\)). Use the slide bar to independently change either \(n_x\) or \(n_y\) quantum number and see the changing wavefunction.
It is important to note that the wavefunctions can be either positive or negative, even though the associated probability density \(p_{n_x, n_y}(x,y)=|\psi_{n_x, n_y}(x,y)|^2\) is strictly positive.
Figure \(\PageIndex{2}\): Visualizing the first six wavefunctions and associated probability densities for a particle in a two-dimensional square box (\(L_x=L_y=L\)). Use the slide bar to independently change either \(n_x\) or \(n_y\) quantum number and see the changing wavefunction.
Unlike in the one-dimensional analoge, where nodes in the wavefunction are points where \(\psi_{n}(x)=0\), here entire lines can be nodal (called nodal lines). For example, in the state \(\psi_{2,1}(x,y)\), there is a nodal line at \(\psi_{2,1}(L/2,y)\). Along the entire line \(x=L/2\), the wavefunction is \(0\) independent of the value of \(y\). The wavefunction \(\psi_{2,2}(x,y)\) has two nodal lines when \(x=L/2\) and when \(y=L/2\). The sign of the wavefunction and its nodal structure will play central roles later when we consider chemical bonding.
The fact that the wavefunction \(\psi_{n_x n_y}(x,y)\) is a product of one-dimensional wavefunctions:
\[\psi_{n_x n_y}(x,y)=\psi_{n_x}(x)\psi_{n_y}(y)\]
makes the calculation of probabilities rather easy. The probability that a measurement the particle's position will yield a value of \(x \in [a,b]\) and \(y \in [c,d]\) is
\[\begin{align}P(x \in [a,b] \ and \ y \in [c,d]) &= \int_{a}^{b}dx\int_{c}^{d}dy|\psi_{n_x n_y}(x,y)|^2 \nonumber \\ &= \int_{a}^{b}dx\int_{c}^{d}dy\psi_{n_x}^{2}(x)\psi_{n_y}^{2}(y) \nonumber \\ &= \left [ \int_{a}^{b}\psi_{n_x}^{2}(x)dx \right ] \left [ \int_{c}^{d}\psi_{n_y}^{2}(y)dy \right ] \nonumber \end{align} \label{2DProb}\]
For a particle in a two-dimensional square box of length \(L\), if the particle is in the \(\psi_{1,2}(x,y)\) state, what is the probability that a measurement of the particle's position will yield \(x \in [0,L/2]\) and \(y \in [0,L/2]\)?
Solution
Substituting the limits of integration into Equation \ref{2DProb}, we have
\[\begin{align*}P(x \in [0,L/2] \ and \ y \in [0,L/2] &= \left [ \int_{0}^{L/2}\psi_{1}^{2}(x)dx \right ] \left [ \int_{0}^{L/2}\psi_{2}^{2}(y)dy \right ]\\ &= \left [ \dfrac{2}{L}\int_{0}^{L/2}\sin^2 \left ( \dfrac{\pi x}{L} \right ) dx \right ] \left [ \dfrac{2}{L}\int_{0}^{L/2}\sin^2 \left ( \dfrac{2\pi y}{L} \right ) dy \right ]\\ &= \left [ \dfrac{2}{L} \dfrac{L}{4} \right ] \left [ \dfrac{2}{L}\dfrac{L}{4} \right ]\\ &= \dfrac{1}{4}\end{align*}\]
This can be graphically confirmed by exploring the probability densities in Figure \(\PageIndex{2}\) for the \(\psi_{1,2}(x,y)\) state.
For a particle in a two-dimensional square box of length \(L\), if the particle is in the state \(\psi_{2,3}(x,y)\), what is the probability that a measurement of the particle's position will yield \(x \in [0,L/2]\) and \(y \in [0,L/3]\)?
- Answer
-
\[P= \dfrac{1}{6} \nonumber\]
Confirmed this by exploring the probability densities in Figure \(\PageIndex{2}\) for the \(\psi_{2,3}(x,y)\) state.
Note that if the box were rectangular rather than square, then instead of having a length of \(L\) on both sides, there would be two different lengths \(L_x\) and \(L_y\). The formulas for the energies and wavefunctions become only slightly more complicated:
\[E_{n_x, n_y}=\dfrac{\hbar^2 \pi^2}{2m}\left ( \dfrac{n_{x}^{2}}{L_{x}^{2}}+\dfrac{n_{y}^{2}}{L_{y}^{2}} \right ) \label{energy}\]
instead of Equation \ref{squareE} and
\[\psi_{n_x, n_y}(x,y)=\dfrac{2}{\sqrt{L_x L_y}}\sin\left ( \dfrac{n_x \pi x}{L_x} \right ) \sin \left ( \dfrac{n_y \pi y}{L_y} \right ) \]
instead of Equation \ref{squareWF}.
Degeneracy
Two distinct wavefunctions are said to be degenerate if they correspond to the same energy. If the sides a, b of the rectangle are such that a/b is irrational (the general case), there will be no degeneracies. The most degenerate case is the square, \(L_x = L_y\), for which clearly \(E_{m,n} = E_{n,m}\). Degeneracies in quantum physics are most often associated with symmetries in this way. Figure \(\PageIndex{3}\) shows the wavefunctions (3,2) and (2,3) for a rectangle. These are contour maps for the time-independent solution, with white being the highest point. These two wavefunctions do not correspond to the same energy, although they would, of course, for a square.
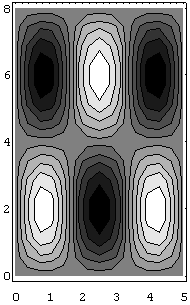
The energy of the particle in a 2-D square box (i.e., \(L_x=L_y=L\)) in the ground state is given by Equation \(\ref{energy}\) with \(n_x=1\) and \(n_y=1\). This energy (\(E_{11}\)) is hence
\[E_{1,1} = \dfrac{2 \hbar^2 \pi^2}{2mL^2} \]
For the ground state of the particle in a 2D box, there is one wavefunction (and no other) with this specific energy; the ground state and the energy level are said to be non-degenerate. However, in the 2-D box potential, the energy of a state depends upon the sum of the squares of the two quantum numbers. The particle having a particular value of energy in the excited state may has several different stationary states or wavefunctions. If so, these states and energy eigenvalues are said to be degenerate.
For the first excited state, three combinations of the quantum numbers \((n_x,\, n_y)\) are \((2,\,1)\) and \((1,2)\). The sum of squares of the quantum numbers in each combination is same (equal to 5). Each waveunction has same energy:
\[E_{2,1} =E_{1,2} = \dfrac{5 \hbar^2 \pi^2}{2mL^2} \]
Corresponding to these combinations three different wavefunctions and two different states are possible. Hence, the first excited state is said to be doubly degenerate. The number of independent wavefunctions for the stationary states with a shared energy is called as the degree of degeneracy of the energy level. The value of energy levels with the corresponding combinations and sum of squares of the quantum numbers
\[n^2 \,= \, n_x^2+n_y^2\]
as well as the degree of degeneracy are depicted in Table \(\PageIndex{1}\).
| \(n_x^2+n_y^2\) | Combinations of Degeneracy (\(n_x\), \(n_y\)) | Total Energy (\(E_{n_x,n_y}\)) | Degree of Degeneracy | ||
|---|---|---|---|---|---|
| 2 | (1, 1) | \(\dfrac{2 \hbar^2 \pi^2}{2mL^2}\) | 1 | ||
| 5 | (2, 1) | (1, 2) | \(\dfrac{5 \hbar^2 \pi^2}{2mL^2}\) | 2 | |
| 8 | (2, 2) | \(\dfrac{8 \hbar^2 \pi^2}{2mL^2}\) | 1 | ||
| 10 | (3, 1) | (1, 3) | \(\dfrac{10 \hbar^2 \pi^2}{2mL^2}\) | 2 | |
| 13 | (3, 2) | (2, 3) | \(\dfrac{13 \hbar^2 \pi^2}{2mL^2}\) | 2 | |
| 18 | (3,3) | \(\dfrac{18 \hbar^2 \pi^2}{2mL^2}\) | 1 | ||
Note that all the states above would be non-degenerate if \(L_x \neq L_y\). However, a degeneracy will be "accidentally" observed for states that fulfill this requirement:
\[ \dfrac{n_x^2}{L_x^2} = \dfrac{n_y^2}{L_y^2}.\]
An electron in a 2D infinite potential well needs to absorb electromagnetic wave with wavelength 4040 nm (IR radiation) to be excited from lowest excited state to next higher energy state. What is the length of the box if this potential well is a square (\(L_x=L_y=L\))?
Solution
The energy of a particle in a 2-D well is given by Equation \ref{energy}:
\[E_{n_x, n_y}=\dfrac{\hbar^2 \pi^2}{2m}\left ( \dfrac{n_{x}^{2}}{L_{x}^{2}}+\dfrac{n_{y}^{2}}{L_{y}^{2}} \right ) \nonumber\]
and for a square well \(L_{x}=L_{y}=L\) this simplifies to Equation \ref{squareE}:
\[E_{n_x, n_y}=\dfrac{\hbar^2 \pi^2}{2mL^2}\left ( n_{x}^{2}+ n_{y}^{2} \right ) \nonumber\]
When the electron absorbs an electromagnetic wave and it transitions from one state (e.g., \((n_x=1,n_y=2)\) or \((n_x=2,n_y=1)\) since are degenerate states as Table \(\PageIndex{1}\) demonstrates) to a higher energetic state, e.g., \((n_x=2,n_y=2\)).
The energy of the lowest excited state is \(\dfrac{5 h^{2}}{8mL^2}\) and the energy of the next higher excited state is \(\dfrac{8 h^{2}}{8mL^2}\), so we can equate the difference in energies of these state to the energy of the absorbed photon
\[ \begin{align*} h\nu &= E_{2,1} - E_{1,1} \\[4pt] &=\dfrac{5\hbar^2 \pi^2}{2mL^2} - \dfrac{2\hbar^2 \pi^2}{2mL^2} \\[4pt] &= \dfrac{3\hbar^2 \pi^2}{2mL^2} \end{align*}\]
Converting frequency (\(\nu\)) to wavelength (\(\lambda\)):
\[ \nu = \dfrac{c}{\lambda} \nonumber\]
results in an expresstion relating wavelength of absorbed light to box length \(L\):
\[ \dfrac{h c}{\lambda}= \dfrac{3 \hbar^2 \pi^2}{2mL^2} \nonumber\]
and solving for \(L\)
\[ L = \sqrt{ \dfrac{3\hbar^2 \pi^2}{2mhc} \lambda} \nonumber\]
or
\[ \begin{align*} L &= \sqrt{ \dfrac{3\hbar \pi}{4mc} \lambda} \\[4pt] &= 1.91\, nm\end{align*}\]
An electron in a 2D infinite potential well needs to absorb electromagnetic wave with wavelength 4040 nm to be excited from \((n_x=2, n_y=2)\) state to the \((n_x=3, n_y=3)\) state.
- What is the length of the box if this potential well is a square (\(L_x=L_y=L\))?
- How many wavefunction exist between these two states (do not count the start or ending states)
- Answer a
-
\(L=3.5\, nm\)
- Answer b
-
From the energies in Table \(\PageIndex{1}\), four wavefunctions exist between \((n_x=2, n_y=2)\) state to the \((n_x=3, n_y=3)\) state. However, due to degeneracy, only two possible energies exist.
Contributors and Attributions
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)


