Photons
- Page ID
- 1690
A photon is a tiny particle that comprises waves of electromagnetic radiation. As shown by Maxwell, photons are just electric fields traveling through space. Photons have no charge, no resting mass, and travel at the speed of light. Photons are emitted by the action of charged particles, although they can be emitted by other methods including radioactive decay. Since they are extremely small particles, the contribution of wavelike characteristics to the behavior of photons is significant. In diagrams, individual photons are represented by a squiggly arrow.
Description
Photons are often described as energy packets. This is a very fitting analogy, as a photon contains energy that cannot be divided. This energy is stored as an oscillating electric field. These fields may oscillate at almost any frequency. Although they have never been observed, the longest theoretical wavelength of light is the size of the universe, and some theories predict the shortest possible at the Planck length. These packets of energy can be transmitted over vast distances with no decay in energy or speed. Photons travel at the speed of light, 2.997x108 m/s in empty space. The speed of a photon through space can be directly derived from the speed of an electric field through free space. Maxwell unveiled this proof in 1864. Even though photons have no mass, they have an observable momentum which follows the de Broglie equation. The momentum of photons leads to interesting practical applications such as optical tweezers.
Generally speaking, photons have similar properties to electromagnetic waves. Each photon has a wavelength and a frequency. The wavelength is defined as the distance between two peaks of the electric field with the same vector. The frequency of a photon is defined as how many wavelengths a photon propagates each second.
Unlike an electromagnetic wave, a photon cannot actually be of a color. Instead, a photon will correspond to light of a given color. As color is defined by the capabilities of the human eye, a single photon cannot have color because it cannot be detected by the human eye. In order for the retina to detect and register light of a given color, several photons must act on it. Only when many photons act in unison on the retina, as an electromagnetic wave, can color be perceived.
As Described by Maxwell's Equations
The most accurate descriptions we have about the nature of photons are given by Maxwell's equations. Maxwell's equations mathematically predict how photons move through space. Fundamentally, an electric field undergoing flux will create an orthogonal magnetic field. The flux of the magnetic field then recreates the electric field. The creation and destruction of each corresponding wave allows the wave pair to move through space at the speed of light. Maxwell's equations correctly describe the nature of individual photons within the framework of quantum dynamics.
Creation of Photons
Photons can be generated in many different ways. This section will discuss some of the ways photons may be emitted. As photons are electric field propagating through space, the emission of photons requires the movement of charged particles.
Blackbody Radiation
As a substance is heated, the atoms within it vibrate at higher energies. These vibrations rapidly change the shape and energies of electron orbitals. As the energy of the electrons changes, photons emitted and absorbed at energies corresponding to the energy of the change. Blackbody radiation is what causes light bulbs to glow, and the heat of an object to be felt from a great distance. The simplification of objects as blackbodies allows indirect temperature calculation of distant objects. Astronomers and kitchen infrared thermometers use this principle every day.
Spontaneous Emission
Photons may be spontaneously emitted when electons fall from an excited state to a lower energy state(usually the ground state). The technical term for this drop in energy is a relaxation. Electrons undergoing this type of emission will produce a very distinctive set of photons based on the available energy levels of their environment. This set of possible photons is the basis for an emission spectrum.
Flourescence
Florescence is special case of spontaneous emission. In florescence, the energy of a photon emitted does not match the energy used to excite the electron. An electron will fluoresce when it loses a considerable amount of energy to its surroundings before undergoing a relaxation. Generally florescence is employed in a laboratory setting to visualize the presence of target molecules. UV light is used to excite electrons, which then emit light at visible wavelengths that researchers can see.
Stimulated Emission
An excited electron can be artificially caused to relax to a lower energy state by a photon matching the difference between these energy states. The electric field's phase and orientation of the resultant photon, as well as its energy and direction will be identical to that of the incident photon. The light produced by stimulated emission is said to be coherent as it is similar in every way to the photon that caused it. Lasers produce coherent electromagnetic radiation by stimulated emission.
Synchrotrons (electron bending)
Electrons with extremely high kinetic energy, such as those in particle accelerators, will produce high energy photons when their path is altered. This alteration is accomplished by a strong magnetic field. All free electrons will emit light in this manner, but synchrotron radiation has special practical implications. Synchrotron radiation is currently the best technology available for producing directional x-ray radiation at precise frequencies. Synchrotrons, such as the Advanced Light Source (ALS) at Lawrence Berkeley Labs and Stanford Synchrotron Radiation Light Source (SSRL) are hotbeds of x-ray spectroscopy due to the excellent quality of x-rays produced.
Nuclear Decay
Certain types of radioactive decay can involve the release of high energy photons. One such type of decay is a nuclear isomerization. In an isomerization, a nucleus rearranges itself to a more stable configuration and emits a gamma ray. While it is only theorized to occur, proton decay will also emit extremely high energy photons.
The Photoelectric Effect
Light incident on a metal plate may cause electrons to break loose from the plate surface (Fig. 1). This interaction between light and electrons is called the photoelectric effect. The photoelectric effect provided the first conclusive evidence that beams of light was made of quantized particles. The energy required to eject an electron from the surface of the metal is usually on the same order of magnitude as the ionization energy. As metals generally have ionization energies of several electron-volts, the photoelectric effect is generally observed using visible light or light of even higher energy.

Fig. 1, The photoelectric effect.
At the time this phenomenon was studied, light was thought to travel in waves. Contrary to what the wave model of light predicted, an increase in the intensity of light resulted in an increase in current, not an increase in the kinetic energy of the emitted electron. Einstein later explained this difference by showing that light was comprised of quantized packets of energy called photons. His work on the photoelectric effect earned him the Nobel Prize.
The photoelectric effect has many practical applications, as current may be generated from a light source. Generally, the photoelectric effect is used as a component in switches that respond to light. Some examples are nightlights and photomultipliers. Usually the current is so small that it must be amplified in order to be an effective switch
Energy of a Photon
The energy of a photon is a discrete quantity determined by its frequency. This result can be determined experimentally by studying the photoelectric effect. The kinetic energy of an emitted electron varies directly with the frequency of the incident light. If the experimental values of these energies are fitted to a line, the slope of that line is Planck's constant. The point at which electrons begin to be emitted from the surface is called the threshold frequency, and is denoted by \(\nu_0\). The principle of conservation of energy dictates that the energy of a photon must all go somewhere. Assuming that the energy \(h\nu_0\) is the initial energy requirement to pry an electron from its orbital, the kinetic energy of a photon is equal to the kinetic energy of the emitted electron plus the ionization energy. Therefore the energy of a free photon becomes \(E = h\nu\) where nu is the frequency of the photon and h is Planck's constant.
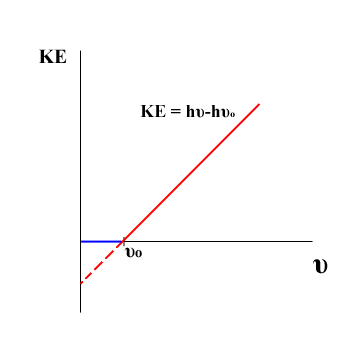
Fig. 2, Photoelectric effect results
The results from a photoelectric experiment are shown in Figure 2. \(\nu_0\) is the minimum frequency at which electrons start to be detected. The solid lines represent the actual observed kinetic energies of released electrons. The dotted red line shows how a linear result can be obtained by tracing back to the y axis. Electrons cannot actually have negative kinetic energies.
Photon Interference
Whereas the double slit experiment initially indicated that a beam of light was a wave, more advanced experiments confirm the electron as a particle with wavelike properties. The diffraction of a beam of light though a double slit is observed to diffract producing constructive and destructive interference. Modern technology allows the emission and detection of single photons. In an experiment conducted by Philippe Grangier, a single photon is passed through a double slit. The photon then is detected on the other side of the slits. Across a large sample size, a trend in the final position of the photons can be determined. Under the wave model of light, an interference pattern will be observed as the photon splits over and over to produce a pattern. However, the results disagree with the wave model of light. Each photon emitted corresponds with a single detection on the other side of the slits(Fig. 3). With a certain probability, each photon is be detected at 100% strength. Over a series of measurements, photons produce the same interference pattern expected of a beam of photons. When one slit is closed, no interference pattern is observed and each photon travels in a linear path through the open slit.
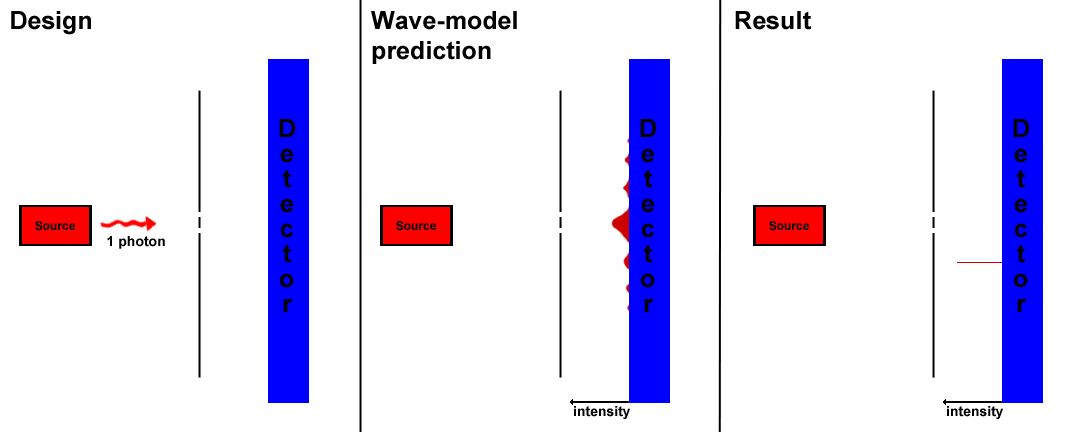
Fig 3, Proof for the particle-nature of photons. One possible result is shown.
This interference has a profound implication which is that photons do not necessarily interact with each other to produce an interference pattern. Instead, they interact and interfere with themselves. Furthermore, this shows that the electron does not pass through one slit or the other, but rather passes through both slits simultaneously. Richard Feynman's theory of quantum electrodynamics explains this phenomenon by asserting that a photon will travel not in a single path, but all possible paths in the universe. The interference between these paths will give the probability of the photon taking any given path, as the majority of the paths cancel with each other. He has used this theory to explain the nature of wide ranges of the actions of photons, such as reflection and refraction, with absolute precision.
References
- Feynman, R. P. (1988). QED: The Strange Theory of Light and Matter, Princeton University Press.
- Einstein, A. . "Über die Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung." Physikalische Zeitschrift(10): 817-825 (1909).
- P. Grangier, G. Roger, and A. Aspect, "Experimental evidence for a photon anticorrelation effect on a beam splitter: A new light on single-photon interferences," Europhys. Lett. 1, 173-179 (1986).
- J. J. Thorn, M. S. Neel, V. W. Donato, G. S. Bergreen, R. E. Davies, and M. Beck, "Observing the quantum behavior of light in an undergraduate laboratory", Am. J. Phys. 72, 1210-1219 (2004).
- Maxwell, James (1865). "A dynamical theory of the electromagnetic field." Philosophical Transactions of the Royal Society of London 155: 459–512.
Problems
1) The peak wavelength of a light bulb is 500 nm. Calculate the energy of a single photon at this wavelength.
Solution
\(E = h\nu\)
\(\nu = \dfrac{c}{\lambda}\)
\(E = h*\dfrac{c}{\lambda}\)
\( = 6.626x10^{-34}m^2kg/s^2*\dfrac{3.00x10^{8}m/s}{500x10^{-9}m}\)
\( = 3.97x10^{-19}J\)
2) The work function of an metal surface is 9.4eV. What is the frequency of a photon which ejects an electron from this surface at 420km/s?
Solution
\(h\nu_0 = 9.4eV x 1.6x10^{-19}J/eV = 1.51x10^{-18} J\)
\(KE = \dfrac{1}{2}mv^2 = h\nu-h\nu_0\)
\(\dfrac{1}{2} ( 9.11x10^{-31}kg)/{(420,000km/s)}^2 = 6.626x10^{-34}m^2kg/s*\nu - 1.51x10^{-18}J\)
\(\nu = 2.28x10^{15}hz\)
3) A single photon passes through a double slit 20nm apart. A photomultiplier detects at least one particle in the 20 nm directly behind the slit. What fraction of the photon is detected here?
Solution
The entire photon is detected. Protons are quantized particles. Although they can pass through both slits, it is still a single particle and will be detected accordingly.
4) A photon removes an electron from an atom. The kinetic energy of the exiting electron is found to be less than that of the photon that removed it. Why isn't the energy the same?
Solution
Recall the photoelectric equation : \(KE = h\nu-h\nu_0\). This equation relates the energies of photons and electrons from an ejection. The second term of the equation, \(-h\nu_0\) is the amount of energy required to remove an electron from its orbital. The extra energy goes into breaking the association of an electron with a nucleus. Keep in mind that for a metal this is not the ionization energy due to the delocalization of electrons involved in metallic bonding.
5) Keeping in mind the relationship between the energy and frequency of light, design an experiment to determine if photons lose energy as they travel through space.
Solution
One possible experiment utilizes the photoelectric effect. A light source is shone on a piece of metal, and the kinetic energy of ejected electrons is calculated. By shining the light at different distances from the metal plate, individual photons may be shown to undergo lossless transmission. The experiment will show that while the number of electrons ejected may decrease as a function of distance, their kinetic energy will remain the same.
Contributors and Attributions
- Michael Kennedy

