Contact Angles
- Page ID
- 1501
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Contact angle is one of the common ways to measure the wettability of a surface or material. Wetting refers to the study of how a liquid deposited on a solid (or liquid) substrate spreads out or the ability of liquids to form boundary surfaces with solid states. The wetting, as mentioned before is determined by measuring the contact angle, which the liquid forms in contact with the solids or liquids. The wetting tendency is larger, the smaller the contact angle or the surface tension is. A wetting liquid is a liquid that forms a contact angle with the solid which is smaller then 90º. A non-wetting liquid creates a contact angle between 90º and 180º with the solid.
Introduction
The contact angle is an angle that a liquid creates with a solid surface or capillary walls of a porous material when both materials come in contact together. This angle is determined by both properties of the solid and the liquid and the interaction and repulsion forces between liquid and solid and by the three phase interface properties (gas, liquid and solid). Those interactions are described by cohesion and adhesion forces which are intermolecular forces. The balance between the cohesive forces of similar molecules such as between the liquid molecules (i.e., hydrogen bonds and Van der Waals forces) and the adhesive forces between dissimilar molecules such as between the liquid and solid molecules (i.e., mechanical and electrostatic forces) will determine the contact angle created in the solid and liquid interface. The traditional definition of a contact angle is the angle a liquid creates with the solid or liquid when it is deposited on it. A less traditional definition is the angle a liquid creates with the sides of a capillary when it rises in it to create a meniscus.

- The smaller the contact angle - cohesive forces are weaker then adhesive forces and molecules of the liquid tend to interact more with solid molecules then liquid molecules.
- The larger the contact angle - cohesive forces are stronger then adhesive forces and the molecules of the liquid tend to interact more with each other then with the solid molecules.
Thermodynamics
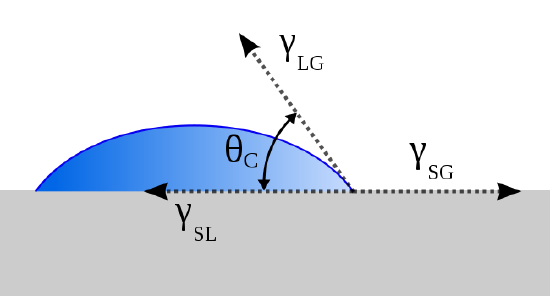
Thomas Young (13 June 1773 – 10 May 1829) proposed treating the contact angle of a liquid with a surface as the mechanical equilibrium of a drop resting on a plane solid surface under the restrains of three surface tensions:
- \(\gamma_{lv}\) (at the interface of the liquid and vapor phases),
- \(\gamma_{sl}\) (at the interface of the solid and liquid phases) and
- \(\gamma_{sv}\) (at the interface of the solid and vapor phase). This lead to Young’s equation:
\[ \gamma_{sv} - \gamma_{sl} = \gamma_{lv} \cos \theta \label{1}\]
This equation is deceptively simple, but there are a few difficulties with it because of the definitions of the surface tension of the solid-vapor and solid liquid phases.
Another approach avoids specifying the field of intermolecular forces between solid and liquid and instead offers a thermodynamic solution. This lead to Young and Dupre’ equation which introduces the reversible work of adhesion of liquid and solid and it’s relation to the surface tension between liquid and vapor phases and the contact angle:
\[ W_{sl}^{adh} = \gamma_{lv} (1 + \cos \theta) \label{2}\]
Where \(WA\) is the reversible work of adhesion of the liquid to the solid when coated with an adsorbed film of the saturated vapor.
Less Traditional Definition
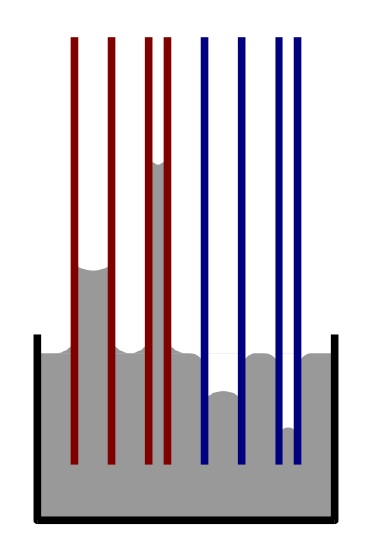
Capillarity is the ability of a substance to draw another substance into it and It occurs when the adhesive intermolecular forces between the liquid and a substance are stronger than the cohesive intermolecular forces inside the liquid. The effect causes a concave meniscus to form where the substance is touching a vertical surface (Figure \(\PageIndex{3}\)). The same effect is what causes porous materials to soak up liquids. Capillary forces pull a wetting liquid has a low contact angle with the surface, it wets the surface. Assuming that there are no other factors involved (e.g. roughness), a low contact angle with water means that the surface is hydrophilic. A completely wetting liquid forms a zero contact angle into a capillary by creating a curved meniscus at the rising liquid front. This phenomenon can be described with the Young-Laplace equation and the Laplace pressure inside a capillary.
Measuring methods
Many measuring methods have been described in the literature but only a few of them have been found to be widely applicable.
The Sessile Drop Method
The most frequently used is the goniometer-telescope measurement of sessile-drop contact angles. Commercial contact angle goniometers employ a microscope objective to view the angle directly. In the static method a drop is deposited on a surface and the contact angle can be measured by looking at the drop through a goniometer (an instrument that measures contact angles). The dynamic method is similar to the static one but the drop of liquid which is deposited on a surface is modified. The droplet is being deposited via a syringe and the droplet’s volume is changed dynamically without increasing its solid-liquid interface area and this maximum angle is the advancing angle. Volume is then removed to produce the smallest possible angle, which is called the receding angle. The difference between those two measured angles is called contact angle hysteresis.
Wilhelmy Plate Method
The capillary rise on a Wilhelmy plate is a good way to obtain the contact angle by measuring the height of the meniscus created on a partially immersed plate. The contact angle is obtained directly form the height trough:
\[ \sin ( \theta) = 1 - \rho g h^2 / 2 \gamma \label{3} \]
where:
- h – height of the meniscus created
- γ - surface tension of the tested liquid (N/m)
- ρ - density of the tested liquid (kg/m3)
- θ - contact angle of the liquid on the solid (º)
- g – gravitational acceleration = 9.8 m/s2
Capillary Rise
The common direct measurement of contact angles of a liquid drop on a flat and smooth solid is not applicable to powders and dry porous foods. The common method of measuring the contact angle in capillary rise in porous media is by using the Lucas-Washburn’s equation which is derived from Poiseulle's law of liquid flow in capillary rise:
\[ h^2 = r c \left( \dfrac{\gamma \cos \theta }{2 \eta} \right) t \label{4}\]
\[ w^2 = c \left( \dfrac{ \rho^2 \gamma \cos \theta }{\eta } \right) t \label{5}\]
where:
- \(h\) – height of the rising liquid
- \(w\) – weight gain of the sample (caused by the water absorbed into it)
- \(γ\) - surface tension of the tested liquid (N/m)
- \(ρ\) - density of the tested liquid (kg/m3)
- \(θ\) - contact angle of the liquid on the solid (º)
- \(r\)- mean static radius of the pores (m)
- \(η\) - liquid viscosity (Pa s)
- \(c\) - geometric factor (m5)
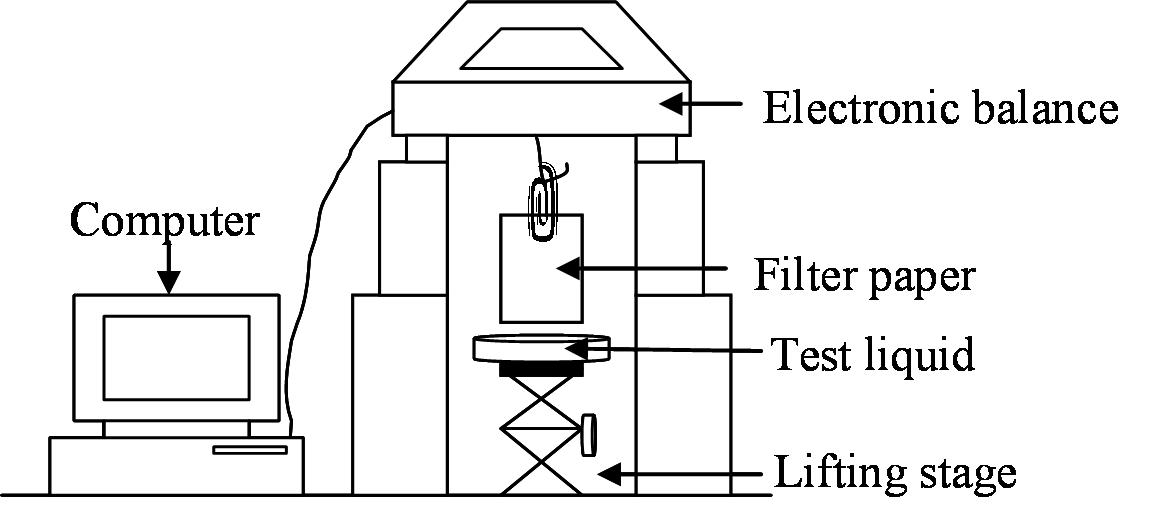
The common method to measure the contact angles in this case is to conduct capillary rise experiments where your sample is hang bellow a balance and you dip it in the tested liquid. The main deficiency of this approach (using Washburn’s equation) is its inability to separate between those two variables (\(r\) and \(\cos θ\) or \(c\) and \(\cos θ\)). The common method to overcome the problem of the unknown term \(r • \cos(θ)\) is by using a reference liquid that completely wets the sample (θ=0, cos(θ)=1). It was discovered however that dynamic advancing contact angle is generally larger than the static one, even for a total wetting liquid and as a result this method can be erroneous.
Seibold et al, (2000) suggested a way to overcome this problem. It was observed that this constant term varies as a function of the liquid used, in contradiction with the Washburn approach which uses Hexane as a completely wetting liquid in order to find the radius of the pores. In this study, it was proposed to get the actual constant term r in Washburn equation by plotting the measured value r cos θ versus the rate of rise of the alkanes (the slope in Equations \ref{4} and \ref{5}). The intercept at zero velocity gives the value of r. Siebold el al. (2000) carried out capillary rise experiments with different n-alkanes, which are all considered completely wetting, due to their low surface tension. In each case, a linear relationship was obtained between squared height of the rising liquid and time, their results of the term \(r•\cos(θ)\) were calculated from the slopes of those curves. This finding was transformed into a method to calculate or measure the contact angle at zero velocity. Siebold et al. (2000) suggested that for porous media the term r•cos(θ) for each alkane (the term was calculated from Washburn equation) can be plotted against the initial front rate of each liquid. The curve that was created can be extrapolated to velocity zero (and therefore, cos(θ)=1) and this enables the determination of the representative radius r. After finding r, which is a property of the solid sample and doesn’t change as a function of the liquids used, we can conduct capillary rise experiment with our test liquid and calculate the contact angles this liquid creates with the solid porous sample.
Applications
The interest in contact angles is because it plays a significant role in a number of technological, environmental and biological phenomena. Water imbibition into porous media theory has been shown to have a multidisciplinary validity in food, soil physics, geology, printings and more. Imbibition of a liquid by a porous solid is a phenomenon highly dependent on wetting. Capillary imbibition is a mechanism that plays a significant role during rehydration of dry food particles that are considered as porous media. Imbibition is highly dependent on the wettability of the porous media, which is usually determined by measuring contact angles which liquids form with the solid.
References
- Adamson, A.W. and Gast A.P. 1997. Physical Chemistry of Surfaces. 6th ed. John Wiley & Sons, NewYork. Pages 352-364.
- Gould, R.F. 1964. Contact angle wettability and adhesion American Chemical Society, USA. Pages 1-4.
- Seibold, A., Nardin, M., Schultz, J., Walliser, A. and Oppliger, M. 2000. Effect of dynamic contact angle on capillary rise phenomena. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 161, 81-87.

