Polarizability
- Page ID
- 40699
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Having now revised the basics of trends across and down the Periodic Table, we can use the concepts of Effective Nuclear Charge and Electronegativity to discuss the factors that contribute to the types of bonds formed between elements.
Fajans' Rules
Rules formulated by Kazimierz Fajans in 1923, can be used to predict whether a chemical bond is expected to be predominantly ionic or covalent, and depend on the relative charges and sizes of the cation and anion. If two oppositely charged ions are brought together, the nature of the bond between them depends upon the effect of one ion on the other.

| Covalent | Ionic |
|---|---|
| Small cation (< ~100 pm) | Large cation (> ~100 pm) |
| Large anion | Small anion |
| High charges | Low charges |
Although the bond in a compound like X+Y- may be considered to be 100% ionic, it will always have some degree of covalent character. When two oppositely charged ions (X+ and Y-) approach each other, the cation attracts electrons in the outermost shell of the anion but repels the positively charged nucleus. This results in a distortion, deformation or polarization of the anion. If the degree of polarization is quite small, an ionic bond is formed, while if the degree of polarization is large, a covalent bond results.
The ability of a cation to distort an anion is known as its polarization power and the tendency of the anion to become polarized by the cation is known as its polarizability. The polarizing power and polarizability that enhances the formation of covalent bonds is favoured by the following factors:
- Small cation: the high polarizing power stems from the greater concentration of positive charge on a small area. This explains why LiBr is more covalent than KBr (Li+ 90 pm cf. K+ 152 pm).
- Large anion: the high polarizability stems from the larger size where the outer electrons are more loosely held and can be more easily distorted by the cation. This explains why for the common halides, iodides, are the most covalent in nature (I- 206 pm).
- Large charges: as the charge on an ion increases, the electrostatic attractions of the cation for the outer electrons of the anion increases, resulting in the degree of covalent bond formation increasing.
Reminder. Large cations are to be found on the bottom left of the periodic table and small anions on the top right. The greater the positive charge, the smaller the cation becomes and the ionic potential is a measure of the charge to radius ratio.
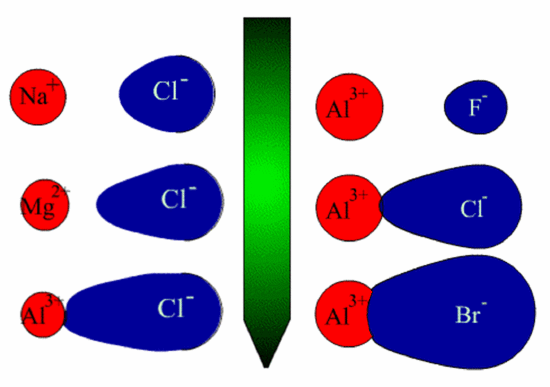
The cation charge increases (size decreases) and on the right, the anion size increases, both variations leading to an increase in the covalency. Thus covalency increases in the order:
[Na+ Cl-, NaCl] < [Mg2+ 2(Cl)-, MgCl2] < [Al3+ 3(Cl)-, AlCl3] and [Al3+ 3(F)-, AlF3] < [Al3+ 3(Cl)-, AlCl3] < [Al3+ 3(Br)-, AlBr3]
Electronic configuration of the cation: for two cations of the same size and charge, the one with a pseudo noble-gas configuration (with 18 electrons in the outer-most shell) will be more polarizing than that with a noble gas configuration (with 8 electrons in the outermost shell). Thus zinc (II) chloride ( Zn(II) 1s2 2s2 2p6 3s2 3p6 3d10 and Cl- 1s2 2s2 2p6 3s2 3p6 ) is more covalent than magnesium chloride ( Mg(II) 1s2 2s2 2p6) despite the Zn2+ ion (74 pm) and Mg2+ ion (72 pm) having similar sizes and charges.
From an MO perspective, the orbital overlap disperses the charge on each ion and so weakens the electrovalent forces throughout the solid, this can be used to explain the trend seen for the melting points of lithium halides.
LiF = 870 °C, LiCl = 613 °C, LiBr = 547 °C, LiI = 446 °C
It is found that the greater the possibility of polarization, the lower is the melting point and heat of sublimation and the greater is the solubility in non-polar solvents.
The melting point of KCl is higher than that of AgCl though the crystal radii of Ag+ and K+ ions are almost the same.
Solution:
When the melting points of two compounds are compared, the one having the lower melting point is assumed to have the smaller degree of ionic character. In this case, both are chlorides, so the anion remains the same. The deciding factor must be the cation. (If the anions were different, then the answer could be affected by the variation of the anion.) Here the significant difference between the cations is in their electronic configurations. K+= [Ar] and Ag+ =[Kr] 4d10. This means a comparison needs to be made between a noble gas core and pseudo noble gas core, which as noted above holds that the pseudo noble gas would be the more polarizing.
Percentage of ionic character and charge distribution
Based on Fajan's rules, it is expected that every ionic compound will have at least some amount of covalent character. The percentage of ionic character in a compound can be estimated from dipole moments. The bond dipole moment uses the idea of electric dipole moment to measure the polarity of a chemical bond within a molecule. It occurs whenever there is a separation of positive and negative charges. The bond dipole μ is given by:
μ = δ d
A bond dipole is modeled as +δ - δ- with a distance d between the partial charges. It is a vector, parallel to the bond axis and by convention points from minus to plus (note that many texts appear to ignore the convention and point from plus to minus). The SI unit for an electric dipole moment is the coulomb-meter, (C m). This is thought to produce values too large to be practical on the molecular scale so bond dipole moments are commonly measured in Debye, represented by the symbol, D.
Historically the Debye was defined in terms of the dipole moment resulting from two equal charges of opposite sign and separated by 1 Ångstrom (10-10 m) as 4.801 D. This value arises from (1.602 x 10-19 * 1 x 10-10) / 3.336 x 10-30 where D = 3.336 x 10-30 C m (or 1 C m = 2.9979 x 1029 D).
Typical dipole moments for simple diatomic molecules are in the range of 0 to 11 D (see Table below).
The % ionic character = μobserved / μcalculated (assuming 100% ionic bond) * 100 %
From the Table below the observed dipole moment of KBr is given as 10.41 D, (3.473 x 10-29 coulomb metre), which being close to the upper level of 11 indicates that it is a highly polar molecule. The interatomic distance between K+ and Br- is 282 pm. From this it is possible to calculate a theoretical dipole moment for the KBr molecule, assuming opposite charges of one fundamental unit located at each nucleus, and hence the percentage ionic character of KBr.
Solution
dipole moment μ = q * e * d coulomb metre
q = 1 for complete separation of unit charge
e = 1.602 x 10-19 C
d = 2.82 x 10-10 m for KBr (282 pm)
Hence calculated μKBr = 1 * 1.602 x 10-19 * 2.82 x 10-10 = 4.518 x 10-29 Cm (13.54 D)
The observed μKBr = 3.473 x 10-29 Cm (10.41 D)
the % ionic character of KBr = 3.473 x 10-29/ 4.518 x 10-29 or 10.41 / 13.54 = 76.87% and the % covalent character is therefore about 23% (100 - 77).
Given the observed dipole moment is 10.41 D (3.473 x 10-29) it is possible to estimate the charge distribution from the same equation by now solving for q:
Dipole moment μ = q * e * d Coulomb meters, but since q is no longer 1 we can substitute in values for μ and d to obtain an estimate for it.
q = μ /(e * d) = 3.473 x 10-29 / (1.602 x 10-19 * 2.82 x 10-10)
thus q = 3.473 x 10-29 / (4.518 x 10-29) = 0.77 and the δ- and δ+ are -0.8 and +0.8 respectively.
For HI, calculate the % of ionic character given a bond length = 161 pm and an observed dipole moment 0.44 D.
Solution
To calculate μ considering it as a 100% ionic bond
μ = 1 * 1.602 x 10-19 * 1.61 x 10-10 / (3.336 x 10-30) = 7.73 D
the % ionic character = 0.44/7.73 * 100 = 5.7%
The calculated % ionic character is only 5.7% and the % covalent character is (100 - 5.7) = 94.3%. The ionic character arises from the polarizability and polarizing effects of H and I. Similarly, knowing the bond length and observed dipole moment of HCl, the % ionic character can be found to be 18%. Thus it can be seen that while HI is essentially covalent, HCl has significant ionic character.
Note that by this simplistic definition, to achieve 100 % covalent character a compound must have an observed dipole moment of zero. Whilst not strictly true for heteronuclear molecules it does provide a simple qualitative method for predicting the bond character.
Bond character based on electronegativity differences
It is possible to predict whether a given bond will be non-polar, polar covalent, or ionic based on the electronegativity difference, since the greater the difference, the more polar the bond.
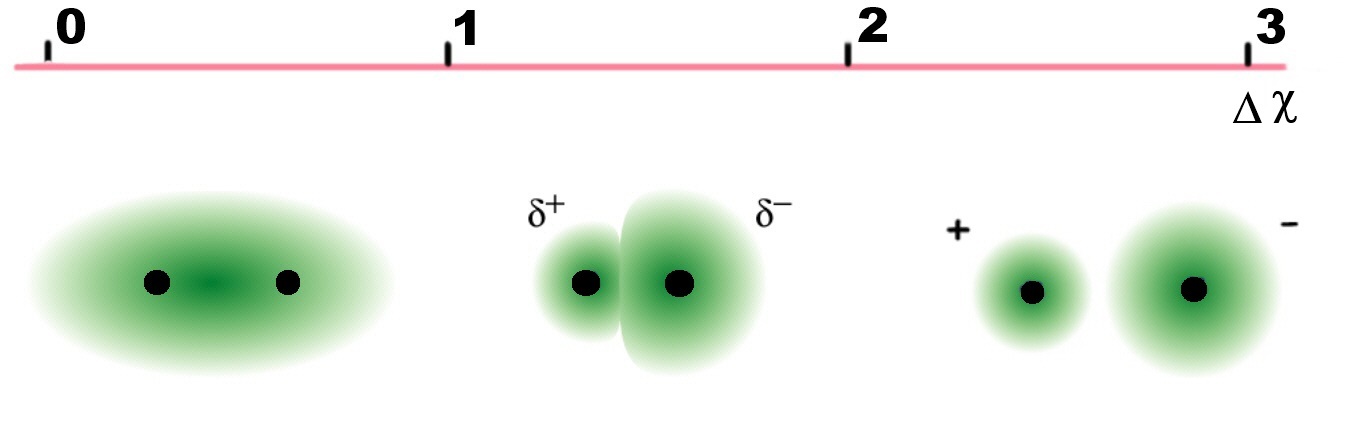
| Electronegativity difference, ΔχP | Bond |
|---|---|
| Δχ < 0.4 | covalent |
| 0.4 < Δχ < 1.7 | polar covalent |
| Δχ > 1.7 | ionic |
Linus Pauling proposed an empirical relationship which relates the percent ionic character in a bond to the electronegativity difference.
percent ionic character= (1-e-(Δχ/2)^2 )* 100
This is shown as the curve in red below and is compared to the values for some diatomic molecules calculated from observed and calculated dipole moments.
| diatomic | Δ χ | %ionic | bond dist /pm | Obs μ /D | Calc μ /D |
|---|---|---|---|---|---|
| Cl2 | 0.0 | 0.0 | 200 | 0.00 | 9.60 |
| IBr | 0.3 | 5.9 | 247 | 0.70 | 11.86 |
| HI | 0.4 | 5.7 | 161 | 0.44 | 7.73 |
| ICl | 0.5 | 5.4 | 232 | 0.60 | 11.14 |
| HBr | 0.7 | 12.1 | 141 | 0.82 | 6.77 |
| HCl | 0.9 | 17.7 | 127 | 1.08 | 6.10 |
| ClF | 1.0 | 11.2 | 163 | 0.88 | 7.83 |
| BrF | 1.2 | 15.1 | 178 | 1.29 | 8.55 |
| LiI | 1.5 | 65.0 | 238 | 7.43 | 11.43 |
| HF | 1.9 | 41.2 | 92 | 1.82 | 4.42 |
| LiBr | 1.8 | 69.8 | 217 | 7.27 | 10.42 |
| KI | 1.7 | 73.7 | 305 | 10.80 | 14.65 |
| LiCl | 2.0 | 73.5 | 202 | 7.13 | 9.70 |
| KBr | 2.0 | 76.9 | 282 | 10.41 | 13.54 |
| NaCl | 2.1 | 79.4 | 236 | 9.00 | 11.33 |
| KCl | 2.2 | 80.1 | 267 | 10.27 | 12.82 |
| CsCl | 2.3 | 74.6 | 291 | 10.42 | 13.97 |
| LiF | 3.0 | 86.7 | 152 | 6.33 | 7.30 |
| KF | 3.2 | 82.5 | 217 | 8.60 | 10.42 |
| CsF | 3.3 | 64.4 | 255 | 7.88 | 12.25 |
London dispersion forces
Intermolecular forces are the attractive forces between molecules without which all substances would be gases. The various types of these interactions span large differences in energy and for the halogens and interhalogens are generally quite small. The forces involved in these cases are called London dispersion forces (after Fritz Wolfgang London, 1900-1954). They are derived from momentary oscillations of electron charge in atoms and hence are present between all particles (atoms, ions and molecules).
The ease with which the electron cloud of an atom can be distorted to become asymmetric is termed the molecule's polarizability. The greater the number of electrons an atom has, the farther the outer electrons will be from the nucleus, and the greater the chance for them to shift positions within the molecule. This means that larger nonpolar molecules tend to have stronger London dispersion forces. This is evident when considering the diatomic elements in Group 17, the Halogens. All of these homo-nuclear diatomic elements are nonpolar, covalently bonded molecules. Descending the group, fluorine and chlorine are gases, bromine is a liquid, and iodine is a solid. For nonpolar molecules, the farther you go down the group, the stronger the London dispersion forces.
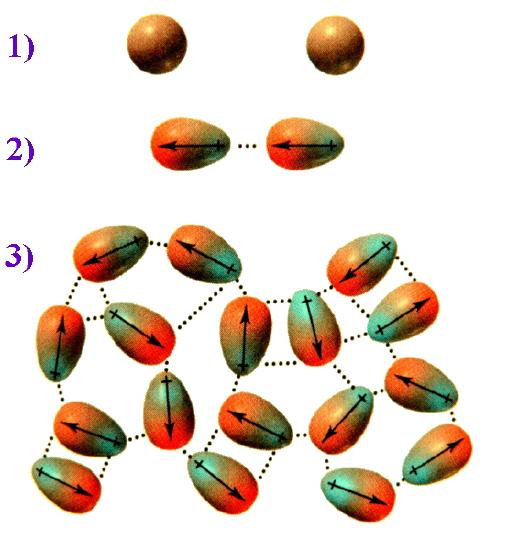
To picture how this occurs, compare the situation 1) where the electrons are evenly distributed and then consider 2) an instantaneous dipole that would arise from an uneven distribution of electrons on one side of the nucleus. When two molecules are close together, the instantaneous dipole of one molecule can induce a dipole in the second molecule. This results in synchronised motion of the electrons and an attraction between them. 3) when this effect is multiplied over numerous molecules the overall result is that the attraction keeps these molecules together, and for diiodine is sufficient to make this a solid.
On average the electron cloud for molecules can be considered to be spherical in shape. When two non-polar molecules approach, attractions or repulsions between the electrons and nuclei can lead to distortions in their electron clouds (i.e. dipoles are induced). When more molecules interact these induced dipoles lead to intermolecular attraction.
The changes seen in the variation of MP and BP for the dihalogens and binary interhalogens can be attributed to the increase in the London dispersion forces of attraction between the molecules. In general they increase with increasing atomic number.

Anomalous behavior of the 2nd row elements: Li, Be, B, C, N, O, F
For the elements in the 2nd row, as the atomic number increases, the atomic radius of the elements decreases, the electronegativity increases, and the ionization energy increases.
The 2nd row has two metals (lithium and beryllium), making it the least metallic period and it has the most nonmetals, with four. The elements in the 2nd row often have the most extreme properties in their respective groups; for example, fluorine is the most reactive halogen, neon is the most inert noble gas, and lithium is the least reactive alkali metal.
These differences in properties with the subsequent rows are a result of:
- the smaller size of the atoms
- an outer shell with a maximum of 8 electrons (2s and 2p) and an underlying shell with just 2 electrons
- no acessible d-orbitals - energy too high for use in bonding
Apart from the 2nd row (ignoring H/He 1st row) the later rows all end with inert gases but these do not have completed quantum levels. The 2nd row elements in general can only use the 2s and 2p electrons for bonding restricting the total number of bonds to 4.
So N is not expected to have more than 4 bonds and 3 is common, while for P 5 and 6 bonded species are quite common.
Reactivity of metals and metalloids
For Lithium, compared to other alkali metals
Reaction with water:
Li reacts slowly with water at 25 °C
Na reacts violently and K in flames
2M(s) + 2H2O(l) → 2M+(aq) + 2OH- + H2(g)
In general Li, Be, B, C, N, O, F are less reactive towards water than their heavier congeners.
Reaction with oxygen:
In conditions of excess oxygen, only Li forms a simple oxide, Li2O. Other metals form peroxides and superoxides
Reaction with nitrogen:
Li reacts directly with N2 to form Li3N
6Li(s) + N2 (g) → 2Li3N(s).
No other alkali metal reacts with N2
Solubility:
LiF, LiOH and Li2CO3 are less soluble than the corresponding Na and K compounds
For Beryllium compared to the other alkaline earth metals:
With water:
All Group 2 metals except Be, react with water
M(s) + 2H2O(l) → M2+(aq)+ 2OH-(aq) + H2 (g)
With oxygen (air):
Be only reacts with air above 600 °C if it is finely powdered. The BeO that is formed is amphoteric (other Group 2 oxides are basic).
Of the Group 2 elements only Be reacts with NaOH or KOH to liberate H2 and form [Be(OH)4]2-.
Li and Be are metals but are less conducting than the higher members of Group 1 and 2 elements due to their high IEs (electrons are close to nucleus).
Ionization of Boron to B3+ requires a large input of energy and B adopts a covalent polymeric structure with semi-metallic properties.
The other elements of Group 14 become increasingly metallic as the group is descended due to the decrease in ionization energies.
Crystalline Boron is chemically inert - unaffected by boiling HCl and only slowly oxidized by hot concentrated HNO3 when finely powdered.
Covalent character
Li+ and Be2+ are small and have strong polarizing abilities. Their compounds are more covalent than those of the heavier elements in their groups.
BeCl2 is covalent while MCl2 (M = Mg-Ba) are ionic. The conductivity of fused beryllium chloride is only 1/1000 that of sodium chloride under similar conditions.
Catenation
Catenation is the linkage of atoms of the same element into longer chains. Catenation occurs most readily in carbon, which forms covalent bonds with other carbon atoms to form longer chains and structures. This is the reason for the presence of the vast number of organic compounds in nature.
The ability of an element to catenate is primarily based on the bond energy of the element to itself, which decreases with more diffuse orbitals (those with higher azimuthal quantum number) overlapping to form the bond. Hence, carbon, with the least diffuse valence shell 2p orbital is capable of forming longer p-p sigma bonded chains of atoms than heavier elements which bond via higher valence shell orbitals.
Hetero-catenation is quite common in Inorganic Chemistry. Phosphates and silicates with P-O-P-O and Si-O-Si-O linkages are examples of this.
Multiple Bonds
C, N and O are able to form multiple bonds (double and/or triple). In Group 14, C=C double bonds are stable (134 pm) but Si=Si double bonds (227 pm) are uncommon. The diagram below shows how multiple bonds are formed involving π overlap of 2p orbitals. By comparison the 3p orbitals of the corresponding third row elements Si, P, and S are more diffuse and the longer bond distances expected for these larger atoms would result in poor π overlap.
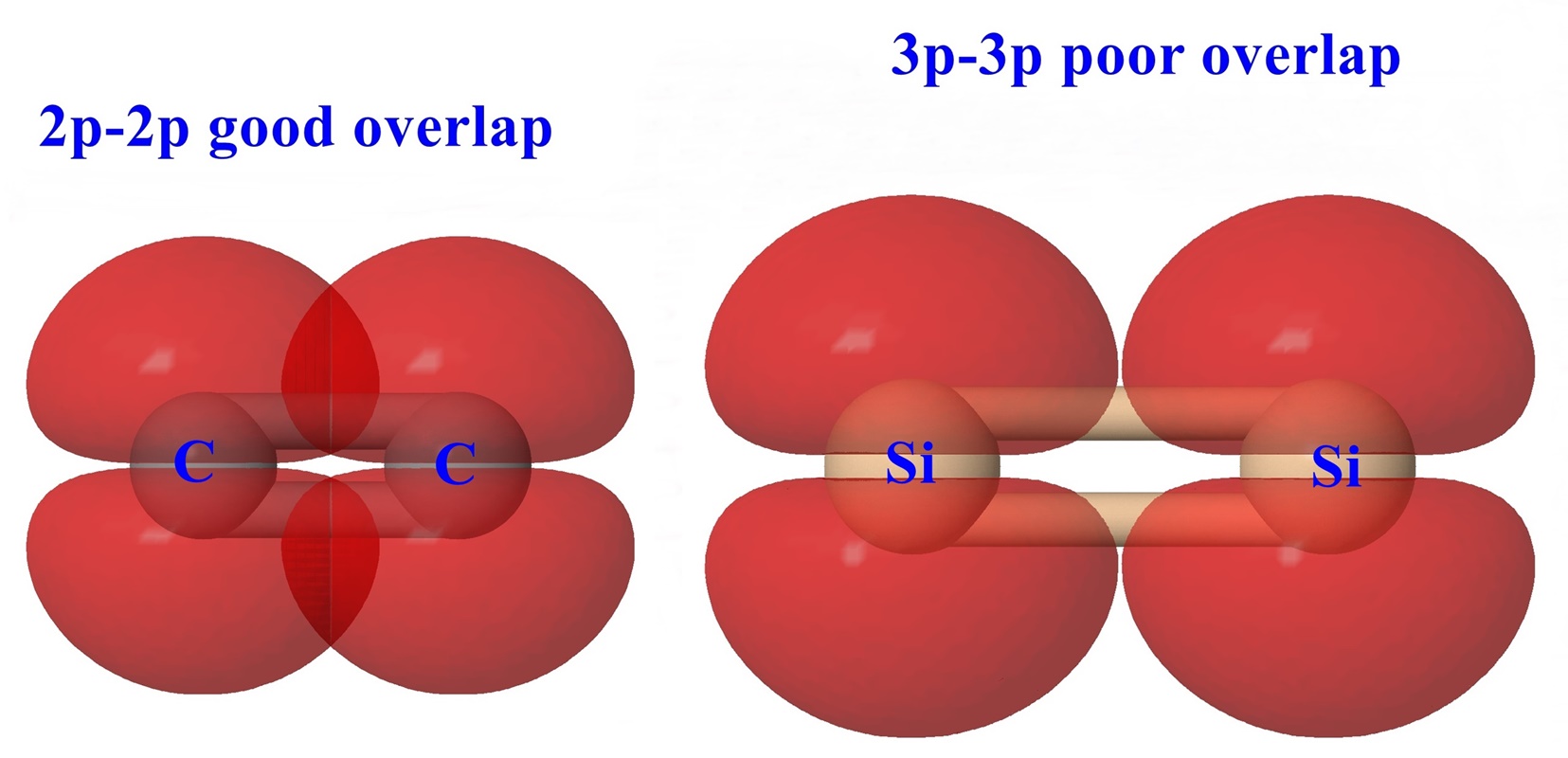
C=C bond length = 134 pm and Si=Si bond length = 227 pm
Oxidizing ability of oxygen and fluorine
Due to the high electron affinities and electronegativities of oxygen and fluorine, they tend to form strong ionic bonds with other elements. They even react with noble gases to form compounds such as XeO3, XeO4, XeF4 and XeF6. In 1962 Neil Bartlett at the University of British Columbia reacted platinum hexafluoride and xenon, in an experiment that demonstrated the chemical reactivity of the noble gases. He discovered the mustard yellow compound, xenon hexafluoroplatinate, which is perhaps now best formulated as a mixture of species, [XeF+][PtF5]-, [XeF+][Pt2F11]-, and [Xe2F3]+[PtF6]-.
A few hundred compounds of other noble gases have subsequently been discovered: in 1962 for radon, radon difluoride (RnF2), and in 1963 for krypton, krypton difluoride (KrF2). The first stable compound of argon was reported in 2000 when argon fluorohydride (HArF) was formed at a temperature of 40 K (-233.2 °C). Neutral compounds in which helium and neon are involved in chemical bonds have still not been formed.
Noble gas compounds have already made an impact on our daily lives. XeF2 is a strong fluorinating agent and has been used to convert uracil to 5-fluorouracil, one of the first anti-tumor agents.


