Mulliken Electronegativity
- Page ID
- 2564
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A method for estimating electronegativity was developed by Robert Mulliken (1896–1986; Nobel Prize in Chemistry 1966) who noticed that elements with large first ionization energies tend to have very negative electron affinities and gain electrons in chemical reactions. Conversely, elements with small first ionization energies tend to have slightly negative (or even positive) electron affinities and lose electrons in chemical reactions. Mulliken recognized that an atom’s tendency to gain or lose electrons could therefore be described quantitatively by the average of the values of its first ionization energy and the absolute value of its electron affinity.
Robert S. Mulliken proposed that the arithmetic mean of the first ionization energy (\(E_{I_1}\)) and the electron affinity (\(E_{ea}\)) should be a measure of the tendency of an atom to attract electrons. As this definition is not dependent on an arbitrary relative scale, it has also been termed absolute electronegativity. Using our definition of electron affinity, we can write Mulliken’s original expression for electronegativity as follows:Mulliken’s definition used the magnitude of the ionization energy and the electron affinity. By definition, the magnitude of a quantity is a positive number. Our definition of electron affinity produces negative values for the electron affinity for most elements, so vertical lines indicating absolute value are needed in Equation \(\ref{1}\) to make sure that we are adding two positive numbers in the numerator.
\[ \chi = \dfrac{|E_{I_1} + E_{ea}|}{2} \label{1}\]
Elements with a large first ionization energy and a very negative electron affinity have a large positive value in the numerator of Equation \(\ref{1}\), so their electronegativity is high. Elements with a small first ionization energy and a small electron affinity have a small positive value for the numerator in Equation \(\ref{1}\), so they have a low electronegativity. Inserting the appropriate data into Equation \(\ref{1}\) gives a Mulliken electronegativity value for fluorine of 1004.6 kJ/mol. To compare Mulliken’s electronegativity values with those obtained by Pauling, Mulliken’s values are divided by 252.4 kJ/mol, which gives Pauling’s value (3.98).
However, it is more usual to use a linear transformation to transform these absolute values into values that resemble the more familiar Pauling values. For ionization energies and electron affinities in electronvolts:
\[\chi_{Mulliken} = 0.187 (E_{I_1}+E_{ea})+0.17 \label{2}\]
and for energies in kJ/mol,
\[\chi_{Mulliken} = (1.97 \times 10^{-3})(E_{I_1}+E_{ea})+0.19 \label{3}\]
The Mulliken electronegativity can only be calculated for an element for which the electron affinity is known, fifty-seven elements as of 2006. The Mulliken electronegativity of an atom is sometimes said to be the negative of the chemical potential. By inserting the energetic definitions of the ionization potential and electron affinity into the Mulliken electronegativity, it is possible to show that the Mulliken chemical potential is a finite difference approximation of the electronic energy with respect to the number of electrons., i.e.,
\[\mu_{Mulliken}= -\chi_{Mulliken} = -\dfrac{E_{I_1} + E_{ea}}{2} \label{4}\]
All electronegativity scales give essentially the same results for one element relative to another. Even though the Mulliken scale is based on the properties of individual atoms and the Pauling scale is based on the properties of atoms in molecules, they both apparently measure the same basic property of an element. In the following discussion, we will focus on the relationship between electronegativity and the tendency of atoms to form positive or negative ions. We will therefore be implicitly using the Mulliken definition of electronegativity. Because of the parallels between the Mulliken and Pauling definitions, however, the conclusions are likely to apply to atoms in molecules as well.
Significance
Despite being developed from a very different set of principles than Pauling Electronegativity, which is based on bond dissociation energies, there is a good correlation between Mullikin and Pauling Electronegativities for the atoms, as shown in the plot below.
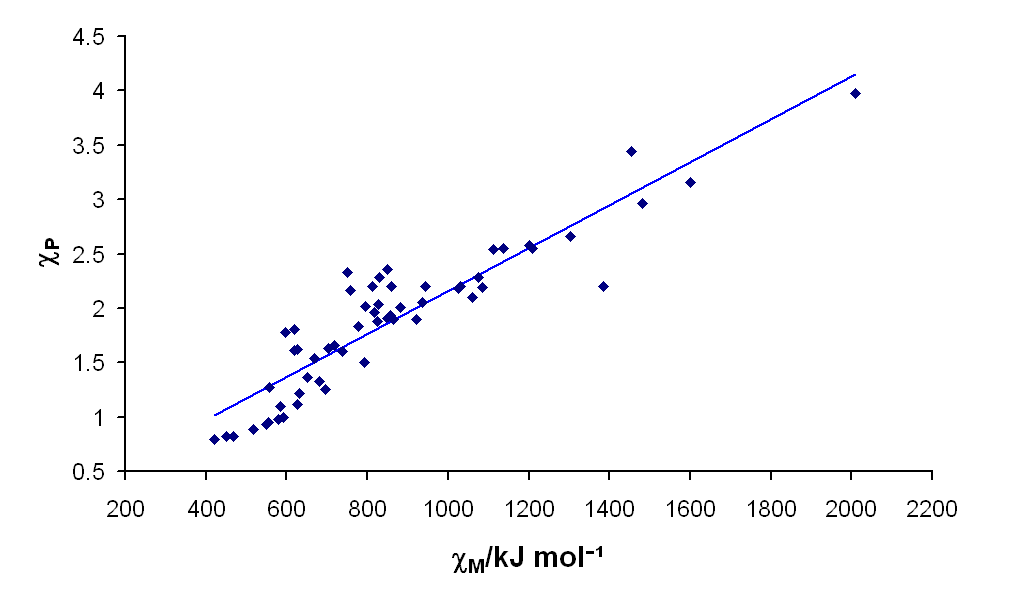
Although Pauling electronegativities are usually what are found in textbooks, the Mullikin electronegativity more intuitively corresponds to the "ability of an atom to draw electrons toward itself in bonding," and is probably a better indicator of that property. However, because of the good correlation between the two scales, using the Pauling scale is sufficient for most purposes.
References
- Mulliken, R. S. (1934). "A New Electroaffinity Scale; Together with Data on Valence States and on Valence Ionization Potentials and Electron Affinities". Journal of Chemical Physics 2 (11): 782–793.
- Mulliken, R. S. (1935). "Electronic Structures of Molecules XI. Electroaffinity, Molecular Orbitals and Dipole Moments". J. Chem. Phys.3 (9): 573–585.
- Pearson, R. G. (1985). "Absolute electronegativity and absolute hardness of Lewis acids and bases". J. Am. Chem. Soc. 107 (24): 6801.
- Huheey, J. E. (1978). Inorganic Chemistry (2nd Edn.). New York: Harper & Row. p. 167.
- This second relation has been recalculated using the best values of the first ionization energies and electron affinities available in 2006.

