6.2.3.3: The Arrhenius Law - Activation Energies
- Page ID
- 1444
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)All molecules possess a certain minimum amount of energy. The energy can be in the form of kinetic energy or potential energy. When molecules collide, the kinetic energy of the molecules can be used to stretch, bend, and ultimately break bonds, leading to chemical reactions. If molecules move too slowly with little kinetic energy, or collide with improper orientation, they do not react and simply bounce off each other. However, if the molecules are moving fast enough with a proper collision orientation, such that the kinetic energy upon collision is greater than the minimum energy barrier, then a reaction occurs. The minimum energy requirement that must be met for a chemical reaction to occur is called the activation energy, \(E_a\).

The reaction pathway is similar to what happens in Figure 1. To get to the other end of the road, an object must roll with enough speed to completely roll over the hill of a certain height. The faster the object moves, the more kinetic energy it has. If the object moves too slowly, it does not have enough kinetic energy necessary to overcome the barrier; as a result, it eventually rolls back down. In the same way, there is a minimum amount of energy needed in order for molecules to break existing bonds during a chemical reaction. If the kinetic energy of the molecules upon collision is greater than this minimum energy, then bond breaking and forming occur, forming a new product (provided that the molecules collide with the proper orientation).
The activation energy (\(E_a\)), labeled \(\Delta{G^{\ddagger}}\) in Figure 2, is the energy difference between the reactants and the activated complex, also known as transition state. In a chemical reaction, the transition state is defined as the highest-energy state of the system. If the molecules in the reactants collide with enough kinetic energy and this energy is higher than the transition state energy, then the reaction occurs and products form. In other words, the higher the activation energy, the harder it is for a reaction to occur and vice versa.
Effects of Enzymes on Activation Energy
However, if a catalyst is added to the reaction, the activation energy is lowered because a lower-energy transition state is formed, as shown in Figure 3. Enzymes can be thought of as biological catalysts that lower activation energy. Enzymes are proteins or RNA molecules that provide alternate reaction pathways with lower activation energies than the original pathways. Enzymes affect the rate of the reaction in both the forward and reverse directions; the reaction proceeds faster because less energy is required for molecules to react when they collide. Thus, the rate constant (k) increases.
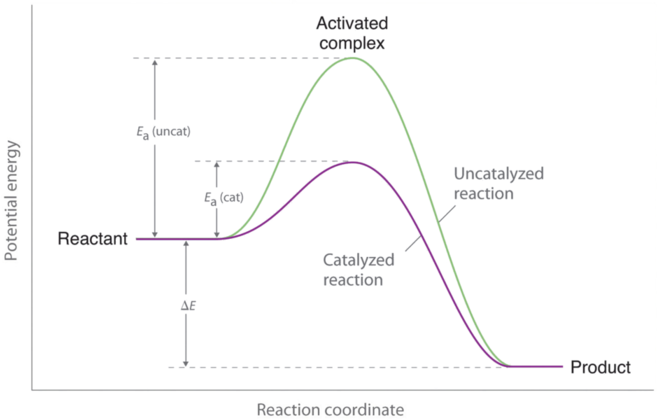
As indicated by Figure 3 above, a catalyst helps lower the activation energy barrier, increasing the reaction rate. In the case of a biological reaction, when an enzyme (a form of catalyst) binds to a substrate, the activation energy necessary to overcome the barrier is lowered, increasing the rate of the reaction for both the forward and reverse reaction. See below for the effects of an enzyme on activation energy.
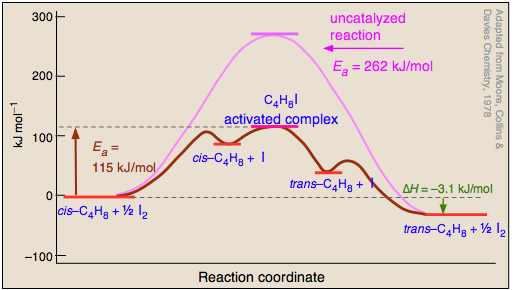
Catalysts do not just reduce the energy barrier, but induced a completely different reaction pathways typically with multiple energy barriers that must be overcome. For example:
Activation Enthalpy, Entropy and Gibbs Energy
In thermodynamics, the change in Gibbs free energy, ΔG, is defined as:
where
\( \Delta G^o \) is the change in Gibbs energy when the reaction happens at Standard State (1 atm, 298 K, pH 7). To calculate a reaction's change in Gibbs free energy that did not happen in standard state, the Gibbs free energy equation can be written as:
\[ \Delta G = \Delta G^o + RT\ \ln K \label{2} \]
where
- ΔG is change in Gibbs free energy of the reaction
- ΔGo is the standard Gibbs free energy
- R is the Ideal Gas constant (8.314 J/mol K)
- \(K\) is the equilibrium constant
When the reaction is at equilibrium, \( \Delta G = 0\). The equation above becomes:
\[ 0 = \Delta G^o + RT\ln K \nonumber \]
Solve for ΔGo:
\[ \Delta G^o = -RT \ln K \nonumber \]
Similarly, in transition state theory, the Gibbs energy of activation, \( \Delta G ^{\ddagger} \), is defined by:
\[ \Delta G ^{\ddagger} = -RT \ln K^{\ddagger} \label{3} \]
and
\[ \Delta G ^{\ddagger} = \Delta H^{\ddagger} - T\Delta S^{\ddagger}\label{4} \]
where
- \( \Delta G^{\ddagger} \) is the Gibbs energy of activation
- \( \Delta H^{\ddagger} \) is the enthalpy of activation
- \( \Delta S^{\ddagger} \) is the entropy of activation
Combining equations 3 and 4 and then solve for \(\ln K^{\ddagger}\) we have the Eyring equation:
\[ \ln K^{\ddagger} = -\dfrac{\Delta H^{\ddagger}}{RT} + \dfrac{\Delta S^{\ddagger}}{R} \nonumber \]
As shown in the figure above, activation enthalpy, \(\Delta{H}^{\ddagger} \), represents the difference in energy between the ground state and the transition state in a chemical reaction. The higher the activation enthalpy, the more energy is required for the products to form. Note that this activation enthalpy quantity, \( \Delta{H}^{\ddagger} \), is analogous to the activation energy quantity, Ea, when comparing the Arrhenius equation (described below) with the Eyring equation:
\[E_a = \Delta{H}^{\ddagger} + RT \nonumber \]
In general, a reaction proceeds faster if Ea and \(\Delta{H}^{\ddagger} \) are small. Conversely, if Ea and \( \Delta{H}^{\ddagger} \) are large, the reaction rate is slower.
Calculation of Ea using Arrhenius Equation
As temperature increases, gas molecule velocity also increases (according to the kinetic theory of gas). This is also true for liquid and solid substances. The (translational) kinetic energy of a molecule is proportional to the velocity of the molecules (KE = 1/2 mv2). Therefore, when temperature increases, KE also increases; as temperature increases, more molecules have higher KE, and thus the fraction of molecules that have high enough KE to overcome the energy barrier also increases.
The fraction of molecules with energy equal to or greater than Ea is given by the exponential term \(e^{\frac{-E_a}{RT}}\) in the Arrhenius equation:
\[k = Ae^{\frac{-E_a}{RT}} \label{5} \]
- k is the rate constant
- Ea is the activation energy
- R is the gas constant
- T is temperature in Kelvin
- A is frequency factor constant or also known as pre-exponential factor or Arrhenius factor. It indicates the rate of collision and the fraction of collisions with the proper orientation for the reaction to occur.
Taking the natural log of both sides of Equation \(\ref{5}\) yields the following:
\[\ln k = \ln A - \frac{E_a}{RT} \label{6} \]
Equation \(\ref{4}\) has the linear form y = mx + b. Graphing ln k vs 1/T yields a straight line with a slope of -Ea/R and a y-intercept of ln A., as shown in Figure 4.
As indicated in Figure 5, the reaction with a higher Ea has a steeper slope; the reaction rate is thus very sensitive to temperature change. In contrast, the reaction with a lower Ea is less sensitive to a temperature change. Because radicals are extremely reactive, Ea for a radical reaction is 0; an arrhenius plot of a radical reaction has no slope and is independent of temperature.
The activation energy can also be calculated directly given two known temperatures and a rate constant at each temperature. Using Equation (2), suppose that at two different temperatures T1 and T2, reaction rate constants k1 and k2:
\[\ln\; k_1 = - \frac{E_a}{RT_1} + \ln A \label{7} \]
and
\[\ln\; k_2 = - \frac{E_a}{RT_2} + \ln A \label{8} \]
Subtract \(ln\; k_2\) from \(ln\; k_1\):
\[ \ln\; k_1 - \ln\; k_2 = \left (- \dfrac{E_a}{RT_1} + \ln A \right ) - \left(- \dfrac{E_a}{RT_2} + \ln A \right) \label{9} \]
After rearrangement:
\[ \ln \left (\dfrac{k_1}{k_2} \right ) = \left(\dfrac{1}{T_2} - \dfrac{1}{T_1}\right)\dfrac{E_a}{R} \label{10} \]
Questions
- Given that the rate constant is 11 M-1s-1 at 345 K and the pre-exponential factor is 20 M-1s-1, calculate the activation energy.
- If a reaction's rate constant at 298K is 33 M-1s-1 and 45 M-1s-1 at 675 K, what is the activation energy?
- What is the Gibbs free energy change at the transition state when ΔH at the transition state is 34 kJ/mol and ΔS at transition state is 66 J/mol at 334K?
- What is the Activation Energy of a reverse reaction at 679K if the forward reaction has a rate constant of 50M-1s-1, a pre-exponential factor of 30M-1s-1, and a ΔH of reaction of 23 kJ/mol?
- Enzymes lower activation energy, and thus increase the rate constant and the speed of the reaction. However, increasing the temperature can also increase the rate of the reaction. Does that mean that at extremely high temperature, enzymes can operate at extreme speed?
Solutions
1. Use the Arrhenius Equation: \(k = Ae^{-E_a/RT}\)
- k is the rate constant, A is the pre-exponential factor, T is temperature and R is gas constant (8.314 J/molK)
- ln(11) = (20)e-Ea/(8.314)(345)
- Ea = 6084.1 J/mol
2. Use the equation: \( \ln \left (\dfrac{k_1}{k_2} \right ) = \dfrac{-E_a}{R} \left(\dfrac{1}{T_1} - \dfrac{1}{T_2}\right)\)
- ln(33/45) = [-Ea/8.314](1/298 - 1/675)
- Ea = 1375.8 J/mol
3. Use the equation \(\Delta{G} = \Delta{H} - T \Delta{S}\)
- \(\Delta{G} = (34 \times 1000) - (334)(66)\)
- \(\Delta{G} = 11956\, J/mol\)
4. Use the equation \(\ln k = \ln A - \dfrac{E_a}{RT}\) to calculate the activation energy of the forward reaction
- ln(50) = (30)e-Ea/(8.314)(679)
- Ea = 11500 J/mol
- Because the reverse reaction's activation energy is the activation energy of the forward reaction plus ΔH of the reaction:
- 11500 J/mol + (23 kJ/mol X 1000) = 34500 J/mol
5. No. Most enzymes denature at high temperatures. At some point, the rate of the reaction and rate constant will decrease significantly and eventually drop to zero. Once the enzyme is denatured, the alternate pathway is lost, and the original pathway will take more time to complete.
References
- Atkins P., de Paua J.. Physical Chemistry for the Life Sciences. pg 256-259. New York. Oxford Univeristy Press. 2006.
- Garrett R., Grisham C. Biochemistry. 3rd Edition. pg 64. California. Thomson Learning, Inc. 2005
- Wade L.G. Organic Chemistry. 6th Edition. pg 139-142. New Jersey. Pearson Prentice Hall. 2006.
Contributors and Attributions
- Matthew Bui, Kan, Chin Fung Kelvin, Sinh Le, Eva Tan

