6.1.1: Collisional Cross Section
- Page ID
- 1403
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The collisional cross section is an "effective area" that quantifies the likelihood of a scattering event when an incident species strikes a target species. In a a hard object approximation, the cross section is the area of the conventional geometric cross section. The collisional cross sections typically denoted σ and measured in units of area.
Introduction
Atoms and molecules can move around in space and bump into each other. If certain conditions of the collision are met, a chemical reaction occurs and a product forms. Sometimes, however, particles may get extremely close to each other but do not strike. We can use the collisional cross section to find how large the distance between two particles must be in order for a collision to occur.
A few assumptions must be made:
- All particles travel through space linearly
- All particles are hard spheres
- Only two particles are involved in the collision
The collisional cross section is defined as the area around a particle in which the center of another particle must be in order for a collision to occur. In the image below, the area within the black circle is molecule A's collisional cross section. That area can change depending on the size of the two particles involved.
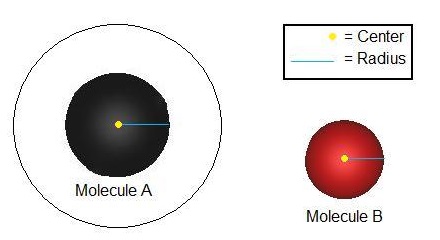
The collisional cross section \(\sigma_{AA}\) between molecule \(A\) and molecule \(A\) can be calculated using the following equation:
\[ \sigma_{AB} = \pi{(r_A + r_B)^2} \nonumber \]
Collision occurs when the distance between the center of the two reactant molecules is less than the sum of the radii of these molecules, as shown in Figure \(\PageIndex{2}\). The collisional cross section describes the area around a single reactant. For a collisional reaction to occur, the center of one reactant must be within the collisional cross section of a corresponding reactant.
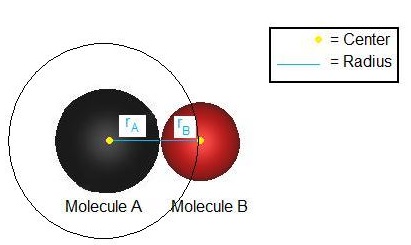
It is first assumed that all particles, whether it be an atom or a molecule, are hard spheres. Particle A must come in contact with Particle B in order for a collision to occur. Particle B can approach particle A from any direction; thus, consider a circle with radius \(r\):
\[Area \; of \; a \; Circle = \pi{r}^2 \nonumber \]
Assume that the two particles involved in the collision are the same in size and have the same radius. The furthest distance the two centers can be and still have a collision is \(2r\). Substitute \(r\) with \(2r\):
\[ \sigma_{AA}= \pi{(2r)}^2 \label{SameEq} \]
We will define this area as the collisional cross section. Anytime the center of another particle is within this area, there will be parts of the two particles that will overlap, touch, and cause a collision.
Consider the following reaction: \(\ce{H + H -> H_2}\) The radius of hydrogen is \(5.3 \times 10^{-11}\; m\). What is the collisional cross section for this reaction?
Solution
Use Equation \ref{SameEq} with the given atomic radius for hydrogen atoms:
\[\text{Collisional Cross Section}= \pi{(2r)}^2= \pi{[(2)(5.3 \times 10^{-11}\,m)]}^2= 3.53 \times 10^{-20} m^2 \nonumber \]
Although the collisional cross section of a particle can be calculated, it is usually not used on its own (Table \(\PageIndex{1}\)). Instead, it is a component of more complex theories such as collision frequency and collision theory.
| Molecule | Cross-Section (nm2) |
|---|---|
| Ar | 0.36 |
| C2H4 | 0.64 |
| C6H6 | 0.88 |
| CH4 | 0.46 |
| Cl2 | 0.93 |
| CO2 | 0.52 |
| H2 | 0.27 |
| He | 0.21 |
| N2 | 0.43 |
| Ne | 0.24 |
| O2 | 0.40 |
| SO2 | 0.58 |
Now what if the particles were of different size and different radii? The \(2r\) term in Equation \(\ref{SameEq}\) is really the sum of the radius of each molecule (i.e., \(2r= r + r\)). However, if the colliding molecules have differing sizes (e.g., \(r_A\) and \(r_B\)) for the radius of particle A and B, respectively, then \(2r\) in Equation \(\ref{SameEq}\) is substituted with \(r_A+r_B\):
\[ \sigma_{AB} = \pi{(r_A + r_B)}^2 \nonumber \]
What is the collisional cross section for this reaction?
\[ H + F \rightarrow HF \nonumber \]
The radius of fluorine atom is 4.2 x 10-11 m.
Solution
\[\text{ Collisional Cross-Section}= \pi{(r_A+r_B)}^2= \pi{[(5.3 \times 10^{-11})+(4.3 \times 10^{-11})]}^2= 2.90 \times 10^{-20} \,m^2 \nonumber \]
\( H_2 + O_2 \rightarrow H_2O \). The radius of oxygen is 4.8 x 10-11 m. What is the collisional cross section for this reaction? (Hint: Assume that the radius of a molecule is just the sum of its atoms.)
- Answer
-
The radius of H2 is 2(rH)=1.06 x 10-10 m. The radius of O2 is 2(rO)=9.6 x 10-11 m. \[Collisional \; Cross \; Section= \pi{(r_A+r_B)}^2= \pi{[(1.06 \times 10^{-10})+(9.6 \times 10^{-11})]}^2= 1.28 \times 10^{-19} \nonumber \]
\( N_2 + O_2 \rightarrow N_2O \). The radius of nitrogen is 5.6 x 10-11 m. If the distance between the two centers is 2.00 x 10-19 m, is there a collision between the two molecules?
- Answer
-
Yes, there is a collision. The radius of N2 is 2(rN)=1.12 x 10-10 m. The radius of O2 is 2(rO)=9.6 x 10-11 m. \[Collisional \; Cross \; Section= \pi{(r_A+r_B)}^2= \pi{[(1.12 \times 10^{-10})+(9.6 \times 10^{-11})]}^2= 1.36 \times 10^{-19} \nonumber \] 1.36 x 10-11 m is the furthest the two molecules can be and still get a collision. Since 2.00 x 10-11 m is larger than that distance, the center of one molecule is not in the collisional cross section of the other molecule. Therefore, no collision occurs. The molecules are too far apart.
\( F + F \rightarrow F_2 \) The center of the two atoms are 3.50 x 10-20 m apart from each other. How much closer do the centers have to be in order for a collision to occur?
- Answer
-
\[Collisional \; Cross \; Section= \pi{(2r)}^2= \pi{[(2)(4.2 \times 10^{-11})]}^2= 2.22 \times 10^{-20} \nonumber \] Because the molecules are 3.50 x 10-20 m apart, the center of one F is not in the Collisional Cross Section of the other F. They must be closer. \[(3.50 \times 10^{-20})-(2.22 \times 10^{-20})=1.28 \times 10^{-20} \nonumber \] The molecules must be at least 1.28 x 10-20 m closer.
References
- Atkins, Peter and Julio de Paula. Physical Chemistry for the Life Sciences. 2006. New York, NY: W.H. Freeman and Company. pp.282-288, 290
- Atkins, Peter. Concepts in Physical Chemistry. 1995. New York, NY: W.H. Freeman and Company. pp.193
- Chang, Raymond. Physical Chemistry for the Biosciences. 2005. Sausalito, CA: University Science Books. pp.28
Contributors and Attributions
- Lily Feng, Keith Dunaway (UC Davis)

