Fluorescence Resonance Energy Transfer
- Page ID
- 2012
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Fluorescence Resonance Energy Transfer (FRET) is a special technique to gauge the distance between two chromophores, called a donor-acceptor pair. The limitation of FRET is that this transfer process is effective only when the separating distance of donor-acceptor pair is smaller than 10 nanometers. However, FRET is a highly distance-dependent phenomenon and thus has become a popular tool to measure the dynamic activities of biological molecules within nanoscale.
Introduction
FRET is the acronym of the Förster (Flourescence) Resonance Energy Transfer. The Förster energy transfer is the phenomenon that an excited donor transfers energy (not an electron) to an acceptor group through a non-radiative process. This process is highly distance-dependent, thus allowing one to probe biological structures. One common application is simply to measure the distance between two positions of interest on a big molecule, generally a biological macromolecule, by attaching appropriate donor-acceptor groups to the big one. If the big molecule only involves one donor and one acceptor group, the distance between the donor and the acceptor can be easily measured if there is no conformational change within this process. Besides, if the molecule has a huge conformational change, one may also measure the dynamical activities between two sites on this macromolecule such as protein interactions. Today, this technique is widely applied in many fields such as single-molecule experiments, molecular motors, biosensors and DNA mechanical movements. FRET is also called the "Spectroscopic Ruler" because of its intrinsic convenience.
The theoretical analysis was well developed by Theodor Förster. This non-radiative transfer mechanism is schematically capsuled in Figure \(\PageIndex{1}\). A donor group (D) is excited by a photon and then relaxes to the lowest excited singlet state, S1 (by Kasha’s rule). If the acceptor group is not too far, the energy released when the electron returns to the ground state (S0) may simultaneously excite the donor group. This non-radiative process is referred to as “resonance”. After excitation, the excited acceptor emits a photon and returns to the ground state, if the other quenching states do not exist.
The resonance mechanism is associated with the Coulombic interaction between electrons. Thus, the relative distance of Coulombic interaction between the donor-acceptor pair could be longer than the electron exchange energy transfer which needs the overlap of wavefunctions, namely the Dexter Energy Transfer. The Coulombic interaction only needs the overlap of the spectrum which means that the identity of resonance energy. Figure \(\PageIndex{2}\) here shall give a sense about what the resonance mechanism is. (Note that the HOMO-LUMO gap does not equal the energy difference between the ground state and the lowest S1 excited state of the molecule.)
Factors that affect FRET
The FRET efficiency (\(E\)) is the quantum yield of the energy transfer transition; i.e., the fraction of energy transfer event occurring per donor excitation event. The FRET efficiency is given by
\[\ E = \dfrac{k_{ET}}{k_f + k_{ET}+\sum k_i} \label{1}\]
where \(k_{ET}\) is the rate of FRET, \(k_f\) is the rate of radiative relaxation (i.e., fluorescence), and \(k_i\) are the non-radiative relaxation rates (e.g., internal conversion, intersystem crossing, external conversion etc). Within a point dipole-dipole approximation, the FRET efficiency can be related to the donar-acceptor distance via
\[\ E = \dfrac{1}{1+\left( \dfrac{r}{R_0} \right)^6} \label{2}\]
where \(r\) is the distance between donor and acceptor chromophores and \(R_o\) is the characteristic distance (the Förster distance or Förster radius) with a 50% transfer efficiency.
Overlap of Spectrum
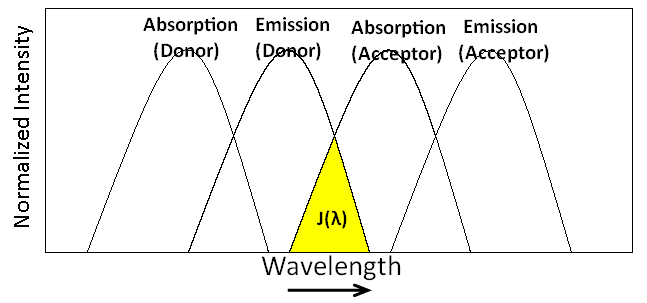
To enhance the FRET efficiency, the donor group should have good abilities to absorb photons and emit photons. That means the donor group should have a high extinction coefficient and a high quantum yield. The overlap of emission spectrum of the donor and absorption spectrum of the acceptor means that the energy lost from excited donor to ground state could excite the acceptor group. The energy matching is called the resonance phenomenon. Thus, the more overlap of spectra, the better a donor can transfer energy to the acceptor. The overlap integral, \(J(λ)\), between the donor and the acceptor stands for the overlap of spectra, as shown in Figure \(\PageIndex{3}\).
The overlap integral is given by
\[ J = \int_o^{\infty} F_D(\lambda)\epsilon_A(\lambda) \lambda^4 \,d\lambda \label{3}\]
where \(F_D(λ)\) is the normalized emission spectrum of the donor, \(\epsilon_{A}\) standards for the molar absorption coefficient of the acceptor, and \(λ\) is the wavelength.
Orientation of Transition Dipoles
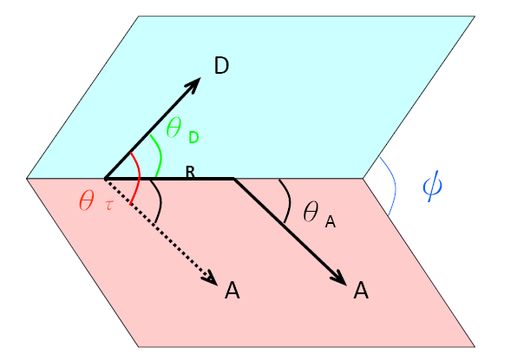
The resonance energy transfer mechanism is also affected by the orientations of the emission transition dipole of the donor and the absorption dipole of the acceptor. The orientation parameter \(κ^2\) gives the quantitative value of interaction between two dipole moments. \(κ^2\) can theoretically be values from 0 (when dipoles are perpendicular to each other) to 4 (when dipoles are collinear).
\[\begin{aligned}
\kappa^{2} &=\left(\cos \theta_{\tau} \cdot 3 \cos \theta_{0} \cos \theta_{A}\right)^{2} \\[4pt]
&=\left(\sin \theta_{0} \sin \theta_{A} \cos \phi \cdot 2 \cos \theta_{0} \sin \theta_{A}\right)^{2}
\end{aligned}\]
\(κ^2\) is equal to 1 when these two transition dipoles are parallel. The orientation of transition dipoles is shown in Figure \(\PageIndex{4}\). For a freely rotational donor and acceptor group, the average \(κ^2\) is treated 2/3.
Förster Distance (R0)
A long \(R_0\) can cause a high FRET efficiency. Based on Förster's analysis, \(R_0\) is a function of quantum yield of the donor chromophore \(\Phi_{D}\), spectral overlap of donor and acceptor \(J(λ)\), directional relationship of transition dipoles \(κ^2\) and the refractive index of the medium \(n\).
\[ (R_0)^6 \propto \kappa^2 \Phi_{D} J(\lambda) n^{-4} \label{4}\]
| Donor | Acceptor |
Förster distance (\(R_0\), nm) |
|---|---|---|
| Naphthalene | Dansyl | 2.2 |
| LY | TNP-ATP | 3.5 |
| Dansyl | ODR | 4.3 |
| LY | EM | 5.3 |
| FITC | EM | 6.0 |
| BPE | CY5 | 7.2 |
Conclusion and the limitations of FRET
FRET provides an efficient way to measure the distance between a donor and an acceptor chromophore. The energy transfer efficiency is highly influenced by the ratio of \(R\) and \(R_0\) because of the exponent 6. Thus, by measuring the FRET efficiency, one can easily get the precise distance between the donor and the acceptor. If choosing the donor and acceptor properly, this experiment can also be carried out in vivo. However, the FRET only gives the information about distances. If a dramatic conformational change happens, such as lengthening or kink, it is unable to know the exact movement of donor and the acceptor. Besides, attaching the chromophores to precise sites of a macromolecule is also important, both in quantity of chromophores and in position of a macromolecule, or the FRET might produce noise signals. (Please refer to question 5)
The F-actin filament is composed by G-actin monomers. By attaching either a donor (D) or an acceptor (A) choromophore to the G-actin monomer and measuring the energy transfer efficiency to gauge the average distance between G-actin monomers in a F-actin filment (assuming that the monomers are well arranged in DADADADA....sequence), and one finds that the average energy transfer efficiencies is 23%. If the \(R_0\) is 4.5 nm, what is the average distance between monomers in a filament?
- Answer
-
5.5 nm.
Based on the question 1, if the filament sequence is composed by 8 monomers in the order of D-A-D-A-D-A-D-A, how many kinds of efficiencies might be detected if the filament does not bend and the \(R_0\) is big enough to see all of them?
- Answer
-
4 kinds of efficiencies will be detected.
The cy3-dornor and cy5-acceptor pair is attached onto the theminals of a DNA sequence. If ignoring the orientations of transition dipoles of donor and acceptor, please plot the relationship between the ratio (\(R/R_0\)) and the energy transfer efficiency.
- Answer
-
Please refer to Professor Taekjip Ha's website. netfiles.uiuc.edu/tjha/www/newTechnique.html
Use the example in question 3, and now consider the orientations of transition dipoles. Please plot the relationship between the separating distance of donor-acceptor pair and the energy transfer efficiency. (Remember that when elongating the DNA by adding base pairs, the orientations of donor and acceptor chromophores will change) (Question 3 and 4 are revised from a paper which measured the orientation dependence in FRET process by using the DNA helix.
- Answer
-
Please refer to PNAS, 2008 Aug, 105(32), 11176-11181, doi:10.1073/pnas.0801707105
One of the most challenging problems within ion channels field is to observe how the channel works in vivo and the conformational change of the channel which is embedded on the cell membrane . If a scientist wants to investigate the movement of the ion channel gate by using FRET, what kinds of factors should be considered? For example, how to attached a proper donor and acceptor to precise positions of the channel gate.
- Answer
-
An open question. Please refer to this introductory paper about using FRET to investigate the ion channel movements. Biophysical Journal, 2003 Jan., 84(1), 1-2, doi:10.1016/S0006-3495(03)74827-9
Footnotes
- PNAS, 2006 Dec., 103(49), 18458-18463, doi: 10.1073/pnas.0605422103
- PNAS, 2008 Nov., 105(47), 18337-18342, doi: 10.1073/pnas.0800977105
- Nature Biotechnology 2003, 21, 1387-1395, doi:10.1038/nbt896
- PNAS, 2009 Oct., 106(42), 17741-17746, doi: 10.1073/pnas.0905177106
- Nature, 1997 Aug., 388, 882-887
- PNAS, 2006 Dec., 103(51) 19217-19218, doi: 10.1073/pnas.0609223103
- PNAS, 1967 Aug., 58(2), 719-26. doi:10.1073/pnas.58.2.719
- Analytical Biochemistry, 1994 Apr., 218(1), 1-13, doi:10.1006/abio.1994.1134
- Nature Protocols, 2006 Aug., 1, 911–919, doi:10.1038/nprot.2006.122
- PNAS, 2008 Aug, 105(32), 11176-11181, doi:10.1073/pnas.0801707105
- Biophysical Journal, 2003 Jan., 84(1), 1-2, doi:10.1016/S0006-3495(03)74827-9

