Le Chatelier's Principle and Dynamic Equilbria
- Page ID
- 3836
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page looks at Le Chatelier's Principle and explains how to apply it to reactions in a state of dynamic equilibrium. It covers changes to the position of equilibrium if you change concentration, pressure or temperature. It also explains very briefly why catalysts have no effect on the position of equilibrium. It is important in understanding everything on this page to realize that Le Chatelier's Principle is no more than a useful guide to help you work out what happens when you change the conditions in a reaction in dynamic equilibrium. It does not explain why the system moved to equilibrium.
If a dynamic equilibrium is disturbed by changing the conditions, the position of equilibrium moves to counteract the change.
Using Le Chatelier's Principle with a Change of Concentration
Suppose you have an equilibrium established between four substances A, B, C and D.
\[ \ce{ A + 2B <=> C +D} \nonumber\]
What would happen if you changed the conditions by increasing the concentration of A?
According to Le Chatelier, the position of equilibrium will move in such a way as to counteract the change. That means that the position of equilibrium will move so that the concentration of A decreases again - by reacting it with B and turning it into C + D. The position of equilibrium moves to the right.

This is a useful way of converting the maximum possible amount of B into C and D. You might use it if, for example, B was a relatively expensive material whereas A was cheap and plentiful.
What would happen if you changed the conditions by decreasing the concentration of A?
According to Le Chatelier, the position of equilibrium will move so that the concentration of A increases again. That means that more C and D will react to replace the A that has been removed. The position of equilibrium moves to the left.

This is essentially what happens if you remove one of the products of the reaction as soon as it is formed. If, for example, you removed C as soon as it was formed, the position of equilibrium would move to the right to replace it. If you kept on removing it, the equilibrium position would keep on moving rightwards - turning this into a one-way reaction.
This is not in any way an explanation of why the position of equilibrium moves in the ways described. All Le Chatelier's Principle gives you is a quick way of working out what happens.
Using Le Chatelier's Principle with a Change of Pressure
This only applies to reactions involving gases:
\[ \ce{A(g) + 2B(g) <=> C(g) + D(g)} \nonumber\]
What would happen if you changed the conditions by increasing the pressure?
According to Le Chatelier, the position of equilibrium will move in such a way as to counteract the change. That means that the position of equilibrium will move so that the pressure is reduced again. Pressure is caused by gas molecules hitting the sides of their container. The more molecules you have in the container, the higher the pressure will be. The system can reduce the pressure by reacting in such a way as to produce fewer molecules.
In this case, there are 3 molecules on the left-hand side of the equation, but only 2 on the right. By forming more C and D, the system causes the pressure to reduce. Increasing the pressure on a gas reaction shifts the position of equilibrium towards the side with fewer molecules.

What would happen if you changed the conditions by decreasing the pressure?
The equilibrium will move in such a way that the pressure increases again. It can do that by producing more molecules. In this case, the position of equilibrium will move towards the left-hand side of the reaction.

What happens if there are the same number of molecules on both sides of the equilibrium reaction?
In this case, increasing the pressure has no effect whatsoever on the position of the equilibrium. Because you have the same numbers of molecules on both sides, the equilibrium can't move in any way that will reduce the pressure again.
Again, this is not an explanation of why the position of equilibrium moves in the ways described.
Using Le Chatelier's Principle with a Change of Temperature
For this, you need to know whether heat is given out or absorbed during the reaction. Assume that our forward reaction is exothermic (heat is evolved):
![]()
![]()
This shows that 250 kJ is evolved (hence the negative sign) when 1 mole of A reacts completely with 2 moles of B. For reversible reactions, the value is always given as if the reaction was one-way in the forward direction. The back reaction (the conversion of C and D into A and B) would be endothermic by exactly the same amount.
![]()
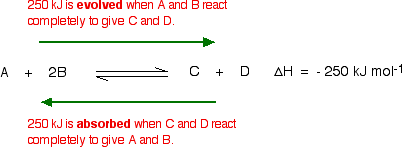
What would happen if you changed the conditions by increasing the temperature?
According to Le Chatelier, the position of equilibrium will move in such a way as to counteract the change. That means that the position of equilibrium will move so that the temperature is reduced again. Suppose the system is in equilibrium at 300°C, and you increase the temperature to 500°C. How can the reaction counteract the change you have made? How can it cool itself down again? To cool down, it needs to absorb the extra heat that you have just put in. In the case we are looking at, the back reaction absorbs heat. The position of equilibrium therefore moves to the left. The new equilibrium mixture contains more A and B, and less C and D.
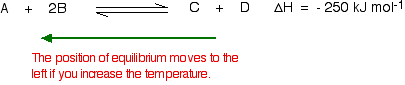
If you were aiming to make as much C and D as possible, increasing the temperature on a reversible reaction where the forward reaction is exothermic is not a good idea!
What would happen if you changed the conditions by decreasing the temperature?
The equilibrium will move in such a way that the temperature increases again. Suppose the system is in equilibrium at 500°C and you reduce the temperature to 400°C. The reaction will tend to heat itself up again to return to the original temperature. It can do that by favoring the exothermic reaction. The position of equilibrium will move to the right. More A and B are converted into C and D at the lower temperature.

Catalysts have sneaked onto this page under false pretenses, because adding a catalyst makes absolutely no difference to the position of equilibrium, and Le Chatelier's Principle does not apply to them. This is because a catalyst speeds up the forward and back reaction to the same extent. Because adding a catalyst does not affect the relative rates of the two reactions, it can't affect the position of equilibrium. So why use a catalyst? For a dynamic equilibrium to be set up, the rates of the forward reaction and the back reaction have to become equal. This does not happen instantly. For a very slow reaction, it could take years! A catalyst speeds up the rate at which a reaction reaches dynamic equilibrium.
Summary
Increasing the temperature of a system in dynamic equilibrium favors the endothermic reaction. The system counteracts the change you have made by absorbing the extra heat. Decreasing the temperature of a system in dynamic equilibrium favors the exothermic reaction. The system counteracts the change you have made by producing more heat. Again, this is not in any way an explanation of why the position of equilibrium moves in the ways described. It is only a way of helping you to work out what happens.
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


