3. The Ionic Product for Water
- Page ID
- 3853
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page explains what is meant by the ionic product for water. It looks at how the ionic product varies with temperature, and how that determines the pH of pure water at different temperatures.
Kw and pKw
Water molecules can function as both acids and bases. One water molecule (acting as a base) can accept a hydrogen ion from a second one (acting as an acid). This will be happening anywhere there is even a trace of water - it doesn't have to be pure. A hydroxonium ion and a hydroxide ion are formed.
However, the hydroxonium ion is a very strong acid, and the hydroxide ion is a very strong base. As fast as they are formed, they react to poduce water again. The net effect is that an equilibrium is set up.
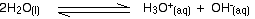
At any one time, there are incredibly small numbers of hydroxonium ions and hydroxide ions present. Further down this page, we shall calculate the concentration of hydroxonium ions present in pure water. It turns out to be 1.00 x 10-7 mol dm-3 at room temperature. You may well find this equilibrium written in a simplified form:
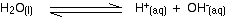
This is OK provided you remember that H+(aq) actually refers to a hydroxonium ion.
Defining the ionic product for water, Kw
Kw is essentially just an equilibrium constant for the reactions shown. You may meet it in two forms:
Based on the fully written equilibrium . . .
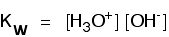
. . . or on the simplified equilibrium:
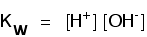
You may find them written with or without the state symbols. Whatever version you come across, they all mean exactly the same thing!
You may wonder why the water isn't written on the bottom of these equilibrium constant expressions. So little of the water is ionised at any one time, that its concentration remains virtually unchanged - a constant. Kw is defined to avoid making the expression unnecessarily complicated by including another constant in it.
The value of Kw
Like any other equilibrium constant, the value of Kw varies with temperature. Its value is usually taken to be 1.00 x 10-14 mol2 dm-6 at room temperature. In fact, this is its value at a bit less than 25°C.
pKw
The relationship between Kw and pKw is exactly the same as that between Ka and pKa, or [H+] and pH.
The Kw value of 1.00 x 10-14 mol2 dm-6 at room temperature gives you a pKw value of 14. Try it on your calculator! Notice that pKw doesn't have any units.
The pH of pure water
Why does pure water have a pH of 7?
That question is actually misleading! In fact, pure water only has a pH of 7 at a particular temperature - the temperature at which the Kw value is 1.00 x 10-14 mol2 dm-6.
This is how it comes about:
To find the pH you need first to find the hydrogen ion concentration (or hydroxonium ion concentration - it's the same thing). Then you convert it to pH. In pure water at room temperature the Kw value tells you that:
[H+] [OH-] = 1.00 x 10-14
But in pure water, the hydrogen ion (hydroxonium ion) concentration must be equal to the hydroxide ion concentration. For every hydrogen ion formed, there is a hydroxide ion formed as well. That means that you can replace the [OH-] term in the Kw expression by another [H+].
[H+]2 = 1.00 x 10-14
Taking the square root of each side gives:
[H+] = 1.00 x 10-7 mol dm-3
Converting that into pH:
pH = - log10 [H+]
pH = 7
That's where the familiar value of 7 comes from.
The variation of the pH of pure water with temperature
The formation of hydrogen ions (hydroxonium ions) and hydroxide ions from water is an endothermic process. Using the simpler version of the equilibrium:
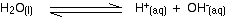
The forward reaction absorbs heat.
According to Le Chatelier's Principle, if you make a change to the conditions of a reaction in dynamic equilibrium, the position of equilibrium moves to counter the change you have made. According to Le Chatelier, if you increase the temperature of the water, the equilibrium will move to lower the temperature again. It will do that by absorbing the extra heat.
That means that the forward reaction will be favored, and more hydrogen ions and hydroxide ions will be formed. The effect of that is to increase the value of Kw as temperature increases. The table below shows the effect of temperature on Kw. For each value of Kw, a new pH has been calculated using the same method as above. It might be useful if you were to check these pH values yourself.
| T (°C) | Kw (mol2 dm-6) | pH |
|---|---|---|
| 0 | 0.114 x 10-14 | 7.47 |
| 10 | 0.293 x 10-14 | 7.27 |
| 20 | 0.681 x 10-14 | 7.08 |
| 25 | 1.008 x 10-14 | 7.00 |
| 30 | 1.471 x 10-14 | 6.92 |
| 40 | 2.916 x 10-14 | 6.77 |
| 50 | 5.476 x 10-14 | 6.63 |
| 100 | 51.3 x 10-14 | 6.14 |
You can see that the pH of pure water falls as the temperature increases.
If the pH falls as temperature increases, does this mean that water becomes more acidic at higher temperatures? NO!
A solution is acidic if there is an excess of hydrogen ions over hydroxide ions. In the case of pure water, there are always the same number of hydrogen ions and hydroxide ions. That means that the water remains neutral - even if its pH changes.
The problem is that we are all so familiar with 7 being the pH of pure water, that anything else feels really strange. Remember that you calculate the neutral value of pH from Kw. If that changes, then the neutral value for pH changes as well.
At 100°C, the pH of pure water is 6.14. That is the neutral point on the pH scale at this higher temperature. A solution with a pH of 7 at this temperature is slightly alkaline because its pH is a bit higher than the neutral value of 6.14. Similarly, you can argue that a solution with a pH of 7 at 0°C is slightly acidic, because its pH is a bit lower than the neutral value of 7.47 at this temperature.