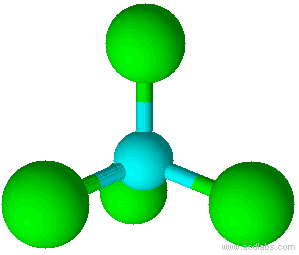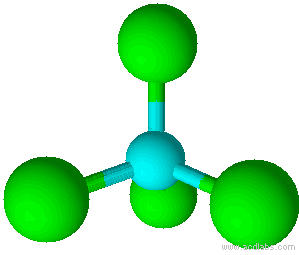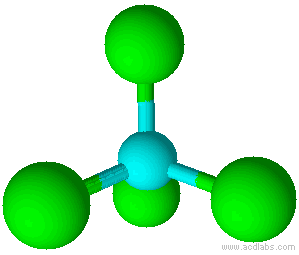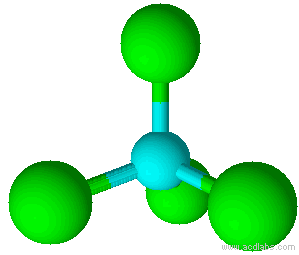
Geometry of Molecules
- Page ID
- 1991
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Molecular geometry, also known as the molecular structure, is the three-dimensional structure or arrangement of atoms in a molecule. Understanding the molecular structure of a compound can help determine the polarity, reactivity, phase of matter, color, magnetism, as well as the biological activity.
Introduction
To determine the shapes of molecules, we must become acquainted with the Lewis electron dot structure. Although the Lewis theory does not determine the shapes of molecules, it is the first step in predicting shapes of molecules. The Lewis structure helps us identify the bond pairs and the lone pairs. Then, with the Lewis structure, we apply the valence-shell electron-pair repulsion (VSPER) theory to determine the molecular geometry and the electron-group geometry.
To identify and have a complete description of the three-dimensional shape of a molecule, we need to know also learn about state the bond angle as well. Lewis Electron Dot Structures play crucial role in determining the geometry of molecules because it helps us identify the valence electrons. To learn how to draw a Lewis electron dot structure click the link above.
Valence-Shell Electron-Pair Repulsion Theory
Now that we have a background in the Lewis electron dot structure we can use it to locate the the valence electrons of the center atom. The valence-shell electron-pair repulsion (VSEPR) theory states that electron pairs repel each other whether or not they are in bond pairs or in lone pairs. Thus, electron pairs will spread themselves as far from each other as possible to minimize repulsion. VSEPR focuses not only on electron pairs, but it also focus on electron groups as a whole. An electron group can be an electron pair, a lone pair, a single unpaired electron, a double bond or a triple bond on the center atom. Using the VSEPR theory, the electron bond pairs and lone pairs on the center atom will help us predict the shape of a molecule.
The shape of a molecule is determined by the location of the nuclei and its electrons. The electrons and the nuclei settle into positions that minimize repulsion and maximize attraction. Thus, the molecule's shape reflects its equilibrium state in which it has the lowest possible energy in the system. Although VSEPR theory predicts the distribution of the electrons, we have to take in consideration of the actual determinant of the molecular shape. We separate this into two categories, the electron-group geometry and the molecular geometry.
Electron-group geometry is determined by the number of electron groups.
| Number of electron groups | Name of electron group geometry |
|---|---|
| 2 | linear |
| 3 | trigonal-planar |
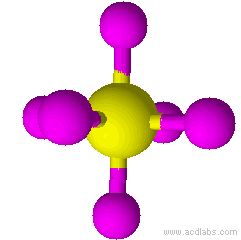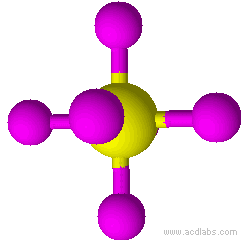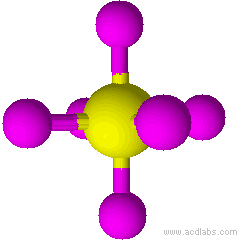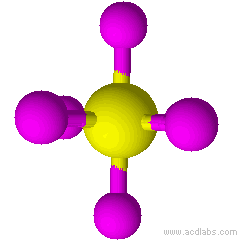
| 4 | tetrahedral |
| 5 | trigonal-bipyramidal |
| 6 | octahedral |
Molecular geometry, on the other hand, depends on not only on the number of electron groups, but also on the number of lone pairs. When the electron groups are all bond pairs, they are named exactly like the electron-group geometry. See the chart below for more information on how they are named depending on the number of lone pairs the molecule has.
VSEPR Notation
As stated above, molecular geometry and electron-group geometry are the same when there are no lone pairs. The VSEPR notation for these molecules are AXn. "A" represents the central atom and n represents the number of bonds with the central atom. When lone pairs are present, the letter Ex is added. The x represents the number of lone pairs present in the molecule. For example, a molecule with two bond pairs and two lone pairs would have this notation: AX2E2.
| Number of Electron Groups | Electron-Group Geometry | Number of Lone Pairs | VSEPR Notation | Molecular Geometry | Ideal Bond Angles | Examples |
|---|---|---|---|---|---|---|
| 2 | linear | 1 | AX2 | 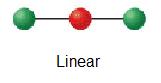 |
180° | BeH2 |
| 3 | trigonal-planar | 0 | AX3 |  |
120° | CO32- |
| 1 | AX2E | 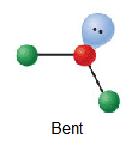 |
120° | O3 | ||
| 4 | tetrahedral | 0 | AX4 |
Tetrahedral |
109.5° | S042- |
| 1 | AX3E | 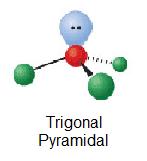 |
109.5° | H3O+ | ||
| 2 | AX2E2 | 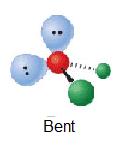 |
109.5° | H2O | ||
| 5 | trigonal-bipyramidal | 0 | AX5 | 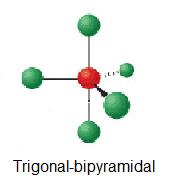 |
90°, 120° | PF5 |
| 1 | AX4Eb | 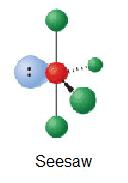 |
90°, 120° | TeCl4 | ||
| 2 | AX3E2 | 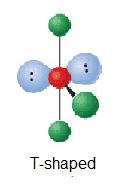 |
90° | ClF3 | ||
| 3 | AX2E3 | 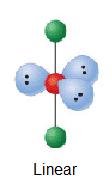 |
180° | I3- | ||
| 6 | octahedral | 0 | AX6 |
octahedral |
90° | PF6- |
| 1 | AX5E | 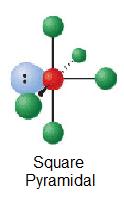 |
90° | SbCl52- | ||
| 2 | AX4E2 | 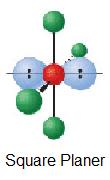 |
90° |
ICl4- |
Lets try determining the geometric structures of H2O and CO2. So starting off by drawing the Lewis structure:
H2O:
Water has four electron groups so it falls under tetrahedral for the electron-group geometry. The four electron groups are the 2 single bonds to Hydrogen and the 2 lone pairs of Oxygen. Since water has two lone pairs it's molecular shape is bent. According to the VSEPR theory, the electrons want to minimize repulsion, so as a result, the lone pairs are adjacent from each other.
CO2:
Carbon dioxide has two electron groups and no lone pairs. Carbon dioxide is therefore linear in electron-group geometry and in molecular geometry. The shape of CO2 is linear because there are no lone pairs affecting the orientation of the molecule. Therefore, the linear orientation minimizes the repulsion forces.
Molecules with More than One Central Atom
The VSEPR theory not only applies to one central atom, but it applies to molecules with more than one central atom. We take in account the geometric distribution of the terminal atoms around each central atom. For the final description, we combine the separate description of each atom. In other words, we take long chain molecules and break it down into pieces. Each piece will form a particular shape. Follow the example provided below:
Butane is C4H10. C-C-C-C is the simplified structural formula where the Hydrogens (not shown) are implied to have single bonds to Carbon. You can view a better structural formula of butane at en.Wikipedia.org/wiki/File:Butane-2D-flat.png
If we break down each Carbon, the central atoms, into pieces, we can determine the relative shape of each section. Let's start with the leftmost side. We see that C has three single bonds to 2 Hydrogens and one single bond to Carbon. That means that we have 4 electron groups. By checking the geometry of molecules chart above, we have a tetrahedral shape. Now, we move on to the next Carbon. This Carbon has 2 single bonds to 2 Carbons and 2 single bonds to 2 Hydrogens. Again, we have 4 electron groups which result in a tetrahedral. Continuing this trend, we have another tetrahedral with single bonds attached to Hydrogen and Carbon atoms. As for the rightmost Carbon, we also have a tetrahedral where Carbon binds with one Carbon and 3 Hydrogens.
Let me recap. We took a look at butane provided by the wonderful Wikipedia link. We, then, broke the molecule into parts. We did this by looking at a particular central atom. In this case, we have 4 central atoms, all Carbon. By breaking the molecule into 4 parts (each part looks at 1 of the 4 Carbons), we determine how many electron groups there are and find out the shapes.
We aren't done, yet! We need to determine if there are any lone pairs because we only looked at bonds. Remember that electron groups include lone pairs! Butane doesn't have any lone pairs. Hence, we have 4 tetrahedrals. Now, what are we going to do with 4 tetrahedrals? Well, we want to optimize the bond angle of each central atom attached to each other. This is due to the electrons that are shared are more likely to repel each other. With 4 tetrahedrals, the shape of the molecule looks like this: en.Wikipedia.org/wiki/File:Butane-3D-balls.png. That means that if we look back at every individual tetrahedral, we match the central Carbon with the Carbon it's bonded to.
Bond Angles
Bond angles also contribute to the shape of a molecule. Bond angles are the angles between adjacent lines representing bonds. The bond angle can help differentiate between linear, trigonal planar, tetraheral, trigonal-bipyramidal, and octahedral. The ideal bond angles are the angles that demonstrate the maximum angle where it would minimize repulsion, thus verifying the VSEPR theory.
Essentially, bond angles is telling us that electrons don't like to be near each other. Electrons are negative. Two negatives don't attract. Let's create an analogy. Generally, a negative person is seen as bad or mean and you don't want to talk to a negative person. One negative person is bad enough, but if you have two put together...that's just horrible. The two negative people will be mean towards each other and they won't like each other. So, they will be far away from each other. We can apply this idea to electrons. Electrons are alike in charge and will repel each other. The farthest way they can get away from each other is through angles. Now, let's refer back to tetrahedrals. Why is it that 90 degrees does not work? Well, if we draw out a tetrahedral on a 2-D plane, then we get 90 degrees. However, we live in a 3-D world. To visualize this, think about movies. Movies in 3D pop out at us. Before, we see movies that are just on the screen and that's good. What's better? 3D or 2D? For bond angles, 3D is better. Therefore, tetrahedrals have a bond angle of 109.5 degrees. How scientists got that number was through experiments, but we don't need to know too much detail because that is not described in the textbook or lecture.
Using the example above, we would add that H2O has a bond angle of 109.5° and CO2 would have a bond angle of 180°.
Steps Used to Find the Shape of the Molecule
To sum up there are four simple steps to apply the VSEPR theory.
- Draw the Lewis Structure.
- Count the number of electron groups and identify them as bond pairs of electron groups or lone pairs of electrons. Remember electron groups include not only bonds, but also lone pairs!
- Name the electron-group geometry. (State whether it is linear, trigonal-planar, tetrahedral, trigonal-bipyramidal, or octahedral.)
- Looking at the positions of other atomic nuclei around the central determine the molecular geometry. (See how many lone pairs there are.)
Dipole Moments
A molecule is polar when the electrons are not distributed equally and the molecule has two poles. The more electronegative end of the molecule is the negative end and the less electronegative end is the positive end. A common example is HCl. Using the capital sigma + or - as a symbol to show the the positive end and the negative end we can draw the net dipole. So sigma + would be on the hydrogen atom and sigma - would be on the Chlorine atom. Using the cross bow arrow shown below we can show that it has a net dipole. The net dipole is the measurable, which is called the dipole moment. Dipole moment is equal to the product of the partial charge and the distance. The equation for dipole moment is as follows.
\[ \mu = \delta \times d\]
with
- µ = dipole moment (debye)
- δ = partial charge (C)
- d = distance (m)
The units for dipole is expressed in debye which is also known as Coulombs x meter (C x m)
Example of a Dipole

The cross base arrow demonstrates the net dipole.
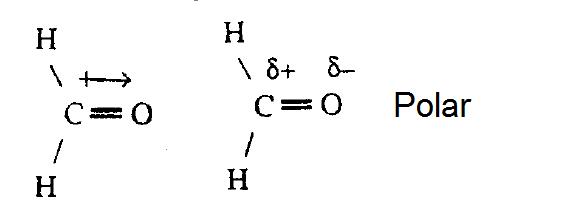
On the cross-base arrow, the cross represents the positive charge and the arrow represents the negative charge.
Here's another way to determine dipole moments. We need to comprehend electronegativity which is abbreviated EN. What is EN? Well, EN is how much an element really wants an electron. Think about basketball and how two players pass the ball to each other. Each player represent an element and the ball represents the electron. Let's say one player is a ball hog. The player that is the ball hog is more electronegative because he or she wants the ball more.
Here is a link that has all the EN listed: www.green-planet-solar-energy...electroneg.gif
What if we are not given EN? Luckily, there is a trend in the periodic table for EN. From bottom to the top, EN will increase. From left to right, EN will increase. The most electronegative element is Flourine with 4.0.
Now, we are ready to apply EN to determine whether or not molecules are polar. We look back at the picture of H2O above. The EN is given. What do we do with all the EN? We compare the EN between each bond. Oxygen has a greater EN than Hydrogen. Therefore, we can draw a cross bow arrow towards Oxygen. We have two arrows because Oxygen is bonded to two Hydrogens. Since both arrows point toward Oxygen, we can say that there is a net EN. We added the arrows that point to Oxygen and we end up with a new, bigger arrow. This is examplified in the picture above. If arrows are drawn away from each other like <--- and --->, then we are more likely to have no net EN because the molecule is symmetrical. Refer back to the Lewis dot diagram of CO2. The shape is linear and the EN arrows point towards Oxygen. The arrows are opposite of each other and have the same EN difference. Therefore, we have no net charge and the molecule is non-polar.
Summary of Dipole Moments
To recap, when a molecule is polar it means that the electron is not distributed evenly and there is a difference in the electronegativity of the atoms. If a molecule is polar, it means that it had a net dipole which results in having a dipole moment.
Determining Polarity
Is it polar? There are three ways to go about determining whether a molecule is polar or not.
A. If the molecule has a net dipole, then it is polar.
B. If the structure is symmetric, then it is non-polar
C. There are three rules to this part:
1. When there are no lone pairs on the center atom, then the molecule is non-polar
2. If it is linear or square planar, then it is non-polar. (This rule is more important than rule 1, so it overrules it because it has lone pairs.)
3. If it has different terminal atoms, then it is polar. (This rule overrules rule 1 and 2 because it is more important.)
References
- Petrucci, Ralph H., William S. Harwood, F. Geoffrey Herring, & Jeffry D. Madura, General Chemistry, Principles and Modern Appplications Ninth Edition, Upper Saddle River, New Jersey
- Tetrahedrality” and the Relationship between Collective Structure and Radial Distribution Functions in Liquid Water P. E. Mason and J. W. Brady J. Phys. Chem. B;2007
- Inverted geometries at carbon Kenneth B. Wiberg Acc. Chem. Res.; 1984
- "Molecular Geometries." Chemistry Foundations and Applications. Volume 3. Farmington, MI:Lagowski, J.J., 2004.
Problems
Part I
Draw the Lewis Structure and name the shape of each compound. Also determine the polarity and whether or not it has a dipole moment.
- HClO3
- SO3
- PCl4
- C2H4
- SnCl3-
Part II
Name the shape and determine whether they are polar or non-polar.
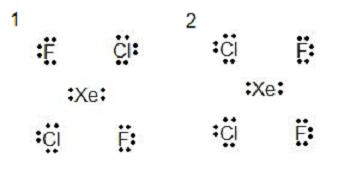
Solutions
Part I
1.
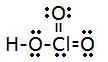
- Total # of electrons: 1+(3x6)+7=26
- electron group geometry: tetrahedral
- molecular: trigonal pyramidal
- ideal angle: 109.5°
- polar, has a dipole moment
2.
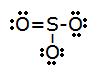
- Total # of electrons: (3x6)+6=24
- electronic group geometry: trigonal planar
- molecular geometry: trigonal planar
- ideal angle: 120°
- polar, has a dipole moment
3.
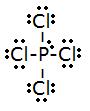
- Total # of electrons: (4x4)+5=19
- electronic group geometry: trigonal-bi-pyramidal
- molecular geometry: seesaw
- ideal angle: 90°, 120°
- polar, has a dipole moment
4.
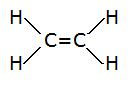
- Total # of electrons: (1x4)+(4x2)=12
- electronic group geometry: trigonal planar
- molecular geometry: trigonal planar
- ideal angle: 120°
- non-polar, does not have a dipole moment
5.
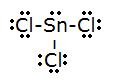
- Total # of electrons: (7x3)+4=26
- electronic group geometry: tetrahedral
- molecular geometry: trigonal pyramidal
- ideal angle: 109.5°
- polar, has a dipole moment.
Part II
1. electron group geometry: octahedral
molecular geometry: square planar
non polar because it is symmetrical
2. electron group geometry: octahedral
molecular geometry: square planar
polar because it is not symmetrical