Electrostatic Potential maps
- Page ID
- 1987
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Electrostatic potential maps, also known as electrostatic potential energy maps, or molecular electrical potential surfaces, illustrate the charge distributions of molecules three dimensionally. These maps allow us to visualize variably charged regions of a molecule. Knowledge of the charge distributions can be used to determine how molecules interact with one another.
Introduction
Electrostatic potential maps are very useful three dimensional diagrams of molecules. They enable us to visualize the charge distributions of molecules and charge related properties of molecules. They also allow us to visualize the size and shape of molecules. In organic chemistry, electrostatic potential maps are invaluable in predicting the behavior of complex molecules.

The first step involved in creating an electrostatic potential map is collecting a very specific type of data: electrostatic potential energy. An advanced computer program calculates the electrostatic potential energy at a set distance from the nuclei of the molecule. Electrostatic potential energy is fundamentally a measure of the strength of the nearby charges, nuclei and electrons, at a particular position.
To accurately analyze the charge distribution of a molecule, a very large quantity of electrostatic potential energy values must be calculated. The best way to convey this data is to visually represent it, as in an electrostatic potential map. A computer program then imposes the calculated data onto an electron density model of the molecule derived from the Schrödinger equation. To make the electrostatic potential energy data easy to interpret, a color spectrum, with red as the lowest electrostatic potential energy value and blue as the highest, is employed to convey the varying intensities of the electrostatic potential energy values.
Analogous System
Electrostatic potential maps involve a number of basic concepts. The actual process of mapping the electrostatic potentials of a molecule, however, involves factors that complicate these fundamental concepts. An analogous system will be employed to introduce these basic concepts.
Imagine that there is a special type of mine. This mine is simply an explosive with some charged components on top of it. The circles with positive and negative charges in them are the charged components. If the electric field of the electric components are significantly disturbed, the mine triggers and explodes. The disarming device is positively charged. To disarm the mine, the disarming device must take the path of least electric resistance and touch the first charged mine component on this path. Deviating from this minimal energy path will cause a significant disturbance and the mine will explode. The specific charged components within the mine are known.
Q. How do you disarm the following mine?
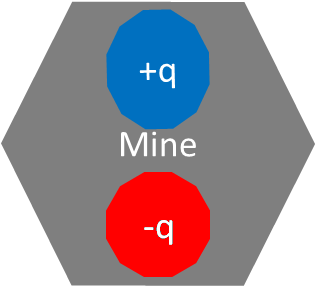
The mine with positive charge and negative charge.
A. Touch the bottom most portion of negatively charged component, red, with the disarming device.
Introduction to Coulomb's Law and Electrostatic Energy
Coulomb's Law Formula
\[F=k \dfrac{q_aq_b}{r^2}\]
with
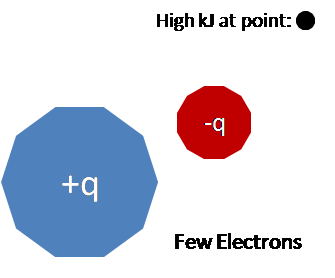
- Molecular electrostatic potential maps also illustrate information about the charge distribution of a molecule. Electrostatic potential maps convey information about the charge distribution of a molecule because of the properties of the nucleus and nature of electrostatic potential energy. For simplicity, consider moving a positively charged test charge along the spherical isosurface of an atom. The positively charged nucleus emits a radially constant electric field. A region of higher than average electrostatic potential energy indicates the presence of a stronger positive charge or a weaker negative charger. Given the consistency of the nucleuses positive charge, the higher potential energy value indicates the absence of negative charges, which would mean that there are fewer electrons in this region. The converse is also true. Thus a high electrostatic potential indicates the relative absence of electrons and a low electrostatic potential indicates an abundance of electrons. This property of electrostatic potentials can be extrapolated to molecules as well.
Here is a simplified visual representation of the relationship between charge distribution and electrostatic potential. Keep in mind the equation used to find the electrostatic potential.
\[ \text{Total Electrostatic Potential Energy= \sum_i \text{Electrostatic Potential Energy} \]
where
\[ \text{Potential Energy}=K \dfrac{q_1q_2}{r}\]
and \(K= \text{Coulomb's Constant}\).

Contributors and Attributions
- Thomas Bottyan

