2.36: Hund's Rule
- Page ID
- 156514
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In a recent discussion of the role of electron–electron repulsion in interpreting chemical reaction mechanisms and spectroscopic phenomena, Liu (1) gives an incorrect answer to the question, Why is the triplet state lower in energy than the corresponding singlet state?
After reviewing the mathematical form of the singlet and triplet wave functions for a two-electron system, Liu presents the plausible and frequently used explanation that the antisymmetric triplet spatial wave function keeps electrons apart while the symmetric singlet spatial wave function permits electrons to be close together. Therefore it follows that electron–electron repulsion must be lower in the triplet state, giving it a lower total energy, E, than the singlet state, which clearly must have greater interelectron repulsion.
Snow and Bills (2) challenged this explanation over thirty years ago with a review of low- and high-level calculations on the 1s12s1 and 1s12p1 excited states of the helium atom available in the research literature. The most accurate calculations (for all practical purposes exact) available for the helium 1s12s1 excited state are shown in Table 1.1 All numerical results are reported in atomic units. (Energy: Eh = 2.626 MJ mol1; distance: a0 = 52.9 pm).
It is obvious that the explanation Liu offers for the relative stability of the triplet state is not supported by accurate quantum mechanical calculations. The electrons are actually closer on average in the triplet state (smaller r12), and consequently electron–electron repulsion (Vee) and electron kinetic energy (T) are higher in the triplet state.2 As the table shows the real reason that the triplet state lies low is due to greater electron–nucleus attraction (Vne). In other words, Vne decreases more than Vee and T increase leading to a more stable triplet state.
Table 1. Expectation Values for the Singlet and Triplet States of the Helium 1s12s1 Excited State Calculated Using the Exact Wave Function
\[ \begin{array}{|c c c c|} \hline \text{Property} & ~^1S & \Delta & ~^3S \\ \hline \langle E \rangle & -2.146 & -0.029 & -2.175 \\ \langle T \rangle & 2.146 & 0.029 & 2.175 \\ \langle V_{ne} \rangle & -4.541 & -0.078 & -4.619 \\ \langle V_{ee} \rangle & 0.250 & 0.018 & 0.268 \\ \langle r_{12} \rangle & 5.270 & -0.822 & 4.448 \\ \hline \end{array} \nonumber \]
Note: All numerical results are reported in atomic units (Energy: Eh = 2.626 MJ mol-1; distance: a0 = 52.9 pm). ∆ = 3S − 1S.
Two questions emerge at this point:
- What is the origin of the incorrect explanation that the results in Table 1 refute?
- How do we “explain” the results in Table 1?
The answer to the first question seems clear in Snow and Bills’ article—first-order perturbation theory. Using zero-order wave functions (the He+ 1s and 2s eigenfunctions) to calculate the singlet and triplet energies of the helium 1s12s1 excited state yields the results shown in Table 2. While this simple calculation correctly shows that the triplet state is more stable than the singlet state, it cannot be safely used for interpretive purposes because it violates the virial theorem, which requires \( \langle E \rangle = - \langleT \rangle = \frac{1}{2} \left[V_{ \text{ne}} + V_{ \text{ee}} \right]. In other words, no physical significance should be attached to the lower interelectron repulsion it yields for the triplet state.
Table 2. Expectation Values for the Singlet and Triplet States of the Helium 1s12s1 Excited State Calculated Using the Zero-Order Wave Function
\[ \begin{array}{|c c c c|} \hline \text{Property} & ~^1S & \Delta & ~^3S \\ \hline \langle E \rangle & -2.036 & -0.088 & -2.124 \\ \langle T \rangle & 2.500 & 0 & 2.500 \\ \langle V_{ne} \rangle & -5.000 & 0 & -5.000 \\ \langle V_{ee} \rangle & 0.464 & -0.088 & 0.376 \\ \langle r_{12} \rangle & 3.085 & 0.046 & 3.131 \\ \hline \end{array} \nonumber \]
In the search for an answer to the second question, we accept guidance from Robert Mulliken’s famous remark (3): “... the more accurate the calculations became, the more the concepts tended to vanish into thin air.” In other words, we seek a level of theory that is quantum mechanically sound and also comprehensible in terms of traditional chemical concepts such as orbitals. The best way to find this theoretical level is to move up gradually from the first-order perturbation theory calculation summarized in Table 2. The calculations that follow have been carried out in the Mathcad programming environment and are available on the Internet (4).
An obvious improvement to the first-order perturbation theory calculation is to add a variational parameter, α, to the 1s and 2s wave functions:
\[ \Psi_{1s} = \sqrt{ \frac{ \alpha^3}{ \pi}} \text{exp} ( \alpha r) \nonumber \]
\[ \Psi_{2s} = \sqrt{ \frac{ \alpha^3}{2 \pi}} (2 - \alpha r) \text{exp} \left( - \frac{ \alpha r}{2} \right) \nonumber \]
Results for such a variational calculation on the 1s12s1 singlet and triplet states of He and Li+ are shown in Table 3.
Table 3. One-Parameter Variational Calculations on He and Li+ Singlet and Triplet States
\[ \begin{array}{|c | c c c| c c c|} \hline \text{Property} & & \text{Helium Atom} & & & \text{Lithium Ion} \\ \hline ~ & ~^1S & \Delta & ~^3S & ~^1S & \Delta & ~^3S \\ \hline \alpha & 1.815 & 0.035 & 1.850 & 2.185 & 0.035 & 2.850 \\ \hline \langle E \rangle & -2.058 & -0.080 & -2.138 & -4.951 & -0.124 & -5.075 \\ \langle T \rangle & 2.508 & 0.088 & 2.138 & 4.951 & 0.124 & 5.075 \\ \langle V_{ne} \rangle & -4.536 & -0.088 & -4.624 & -10.555 & -0.131 & -10.686 \\ \langle V_{ee} \rangle & 0.421 & -0.106 & 0.315 & 0.653 & -0.117 & 0.536 \\ \hline \end{array} \nonumber \]
This calculation shows that the triplet state has a lower energy because both Vne and Vee have lower values in the triplet state. This is a hint that the simple notion that only Vee counts is not valid. This calculation also correctly shows that the triplet state species is smaller (has a larger decay constant α) than the singlet state.
The next step is obvious—a two-parameter calculation that assigns the 2s orbital an independent variational parameter β. The results for this calculation are shown in Table 4. The first thing to note is that this wave function is not quite good enough for He. It shows the singlet state slightly lower in energy than the triplet, but it does show, in agreement with the exact calculations, that Vee is higher for the triplet state. Everything is in order for Li+, showing that Vne is the reason the triplet state lies lower in energy than the singlet because it overwhelms the increases in T and Vee. Additional calculations on Be2+, B3+, and so forth are consistent with the lithium ion results. Given this success it appears justified to use the two-parameter wave function to formulate an answer to the second question.
Table 4. Two-Parameter Variational Calculations on He and Li + Singlet and Triplet States
\[ \begin{array}{|c | c c c| c c c|} \hline \text{Property} & & \text{Helium Atom} & & & \text{Lithium Ion} \\ \hline ~ & ~^1S & \Delta & ~^3S & ~^1S & \Delta & ~^3S \\ \hline 1s ( \alpha ) & 2.013 & -0.019 & 1.994 & 3.019 & -0.020 & 2.999 \\ \hline 2s ( \beta ) & 0.925 & 0.626 & 1.551 & 1.681 & 0.889 & 2.570 \\ \langle E \rangle & -2.170 & 0.003 & -2.167 & -5.091 & -0.012 & -5.103 \\ \langle T \rangle & 2.170 & -0.003 & 2.167 & 5.091 & 0.012 & 5.103 \\ \langle V_{ne} \rangle & -4.594 & -0.026 & -4.620 & -10.629 & -0.055 & -10.684 \\ \langle V_{ee} \rangle & 0.254 & 0.033 & 0.287 & 0.448 & 0.031 & 0.479 \\ \langle r_{1s} \rangle & 0.745 & 0.007 & 0.752 & 0.497 & 0.003 & 0.500 \\ \langle r_{2s} & 6.489 & -2.620 & 3.869 & 3.569 & -1.235 & 2.334 \\ \hline \end{array} \nonumber \]
These calculations show that Vee increases and Vne decreases in going from the singlet to the triplet state. The results also reveal a sharp decrease in the average orbital radius for the 2s electron in the triplet state. These findings are selfconsistent; the antisymmetric character of the triplet state spatial wave function permits a sharp contraction of the 2s orbital increasing the interelectronic repulsion with the 1s electron, but at the same time greatly increasing the favorable attractive interaction between the 2s electron and the nucleus. Shenkuan previously offered a similar analysis on the basis of fourth-order perturbation theory calculations (5). He summarized the results of his study as follows:
In neutral atoms, in many positive ions, and in small molecules, the energy differences among multiplets are dominated by the energy differences in electron–nuclear attractions—not by the energy differences of interelectron repulsions, which was held traditionally.
The singlet–triplet energy difference can be examined further by consideration of the following two-step mechanism using the lithium ion calculation as an example:
\[ \begin{matrix} ~^1S & \left( \alpha = 3.019,~ \beta = 1.681 \right) \\ & \rightarrow ~^3S^* \left( \alpha = 3.019,~ \beta = 1.681 \right) \\ ~ & \rightarrow ~^3S \left( \alpha = 2.999,~ \beta = 2.570 \right) \end{matrix} \nonumber \]
In the singlet–triplet transition two things change: spatial symmetry and orbital size. In the first step the spatial symmetry changes (symmetric to antisymmetric) while the orbitals are frozen at singlet-state size. As shown in Table 5, kinetic energy and electron–electron repulsion decrease, while electron–nucleus and total energy increase. In the second step the orbitals relax to their optimum triplet-state sizes. This net orbital contraction increases kinetic energy and electron–electron repulsion, and decreases electron–nucleus and total energy.
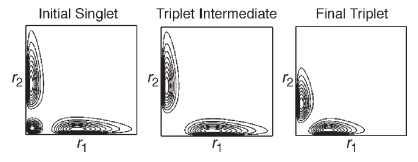
This mechanism is visualized in Figure 1 in which the radial distribution functions3 for the three states are graphed versus the coordinates of both electrons in contour format. The three panes of the figure clearly show the symmetry change and the subsequent orbital contraction, providing visual support for the numeric results presented in Table 5.
Table 5. Mechanism for a Singlet–Triplet Transition for the 1s12s2 Excited State of Li+
\[ \begin{array}{| c c c c c c|} \hline \text{Property} & ~^1S & \Delta & \text{Intermediate} & \Delta & ~^3S \\ \hline 1s ( \alpha ) & 3.019 & 0 & 3.019 & -0.020 & 2.999 \\ 2 s( \beta ) & 1.681 & 0 & 1.681 & 0.889 & 2.570 \\ \langle E \rangle & -5.091 & 0.131 & -4.960 & -0.143 & -5.103 \\ \langle T \rangle & 5.091 & -0.376 & 4.715 & 0.388 & 5.103 \\ \langle V_{ee} \rangle & 0.448 & -0.142 & 0.306 & 0.173 & 0.479 \\ \langle V_{ne} \rangle & -10.629 & 0.649 & -9.980 & -0.704 & -10.684 \\ \hline \end{array} \nonumber \]
Summary
This example teaches the important lesson that an intuitively plausible qualitative explanation may not be correct. Qualitative models for atomic and molecular phenomena require validation by rigorous calculations based on quantum mechanical principles. For example, for the electronic states examined in this study Vee represents less than 4% of the total energy. Vne, the only negative contribution, dominates at about 69% while kinetic energy contributes 31%. In the light of this breakdown it is not surprising that Vee is not the reason for the greater stability of the triplet state.
Notes
- Please consult ref 2 for the appropriate references to the original literature. These can be found in Tables 1 and 2.
- The smaller value for the average interelectron separation for the triplet state implies a smaller atomic volume. Therefore, kinetic energy increases from singlet to triplet because it scales as V-2/3.
- For example, the singlet state spatial wave function can be written as \[ \Psi_s = \left( r_1,~ r_2 \right) = N_s \left[ 1s \left( r_1 \right) 2s \left( r_2 \right) + 2s \left( r_1 \right) 1s \left( r_2 \right) \right] \nonumber \] where r1 and r2 are the coordinates of the electrons and NS is the normalization constant. The singlet state distribution function is \[ R_s \left( r_1,~r_2 \right) \approx \Psi_s \left( r_1,~r_2 \right)^2 r_1^2 r_2^2 \nonumber \] Similar arguments yield the triplet state distribution function.
Literature Cited
- Liu, R. S. H. J. Chem. Educ. 2005, 82, 558–560.
- Snow, R. L.; Bills, J. L. J. Chem. Educ. 1974, 51, 585–586.
- Mulliken, R. S. J. Chem. Phys. 1965, 43, S2.
- Mathcad is a product of Mathsoft Engineering & Education, Inc., 101 Main Street, Cambridge, MA 02142. www.mathsoft.com/. The Mathcad file is available at www.users. csbsju.edu/~frioux/stability/HundsRuleCalc.pdf/.
- Shenkuan, N. J. Chem. Educ. 1992, 69, 800–803.

