Skip to main content
Chemistry LibreTexts

1.87: Planck's Radiation Equation Fit to Experimental Data

  1. Last updated
  2. Save as PDF
  • Page ID
    157655

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    \[
    \mathrm{n} :=42 \qquad \mathrm{i} :=1 . . \mathrm{n}
    \nonumber \]

    \(\rho_{i} :=\) \(\lambda_{i} :=\)
    0.07 0.667
    0.096 00.720
    0.10 0.737
    0.190 0.811
    0.210 0.383
    0.398 0.917
    0.420 0.917
    0.680 1.027
    0.708 1.021
    1.036 1.167
    1.062 1.172
    1.258 1.247
    1.669 1.484
    1.770 1.697
    1.776 1.831
    1.730 2.039
    1.685 2.170
    1.640 2.275
    1.551 2.406
    1.392 2.563
    1.145 2.27
    1.115 2.824
    1.071 2.916
    1.042 2.921
    0.974 3.050
    0.918 2.151
    0.797 3.344
    0.760 3.450
    0.742 3.556
    0.698 3.661
    0.667 3.754
    0.570 4.027
    0.426 4.427
    0.378 4.613
    0.345 4.805
    0.310 4.968
    0.280 5.128
    0.250 5.296
    0.220 5.469
    0.205 5.632
    0.175 5.783
    0.155 6.168

    The data for this exercise is taken from page 19 of Eisberg and Resnick, Quantum Physics.

    The values of rho are given in units of 103 joules/m3 and the values of lambda are given in 10‐6 m. The temperature is 1595 K.

    Two pairs of data points are used to get approximate values for the parameters a and b in the Planck equation.

    \[
    a :=1 \qquad \mathrm{b} :=1
    \nonumber \]

    Given

    \[
    \rho_{16}=\frac{a \cdot\left(\lambda_{16}\right)^{-5}}{e^{\frac{b}{\lambda_{16}}}} \qquad \rho_{22}=\frac{a \cdot\left(\lambda_{22}\right)^{-5}}{e^{\frac{b}{\lambda_{22}}}-1}
    \nonumber \]

    \[
    \left(\begin{array}{l}{\mathrm{a}} \\ {\mathrm{b}}\end{array}\right) :=\text { Find }(\mathrm{a}, \mathrm{b}) \qquad \mathrm{a}=3.84 \times 10^{3} \qquad \mathrm{b}=8.479
    \nonumber \]

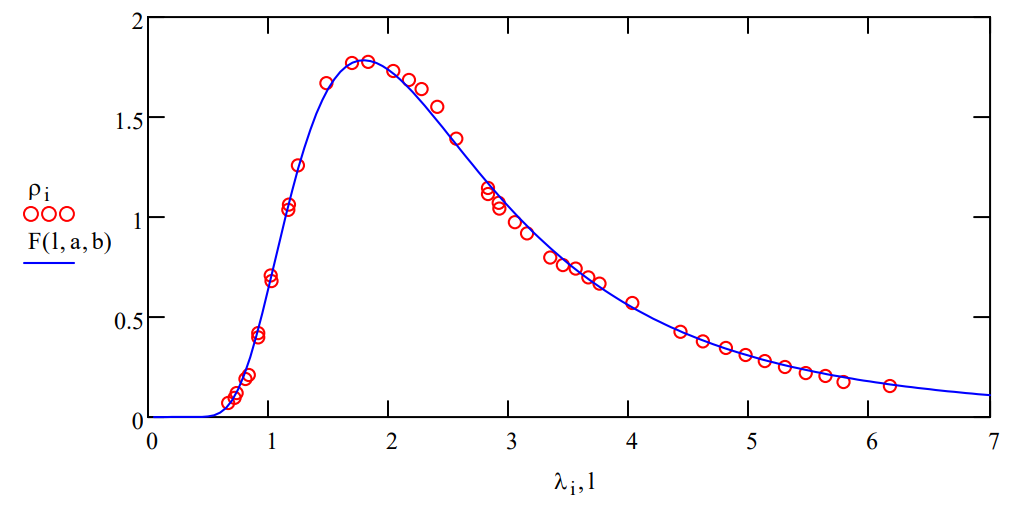
    Planck's Equation is fit to data:

    \[
    \mathrm{F}(\lambda, \mathrm{a}, \mathrm{b}) :=\frac{\mathrm{a} \cdot \lambda^{-5}}{e^{\frac{\mathrm{b}}{\lambda}}-1}
    \nonumber \]

    \[
    \operatorname{SSD}(\mathrm{a}, \mathrm{b}) :=\sum_{\mathrm{i}}\left(\rho_{\mathrm{i}}-\mathrm{F}\left(\lambda_{\mathrm{i}}, \mathrm{a}, \mathrm{b}\right)\right)^{2}
    \nonumber \]

    Given

    \[
    \operatorname{SSD}(\mathrm{a}, \mathrm{b})=0 \qquad \mathrm{a}>0 \qquad \mathrm{b}>0 \qquad\left(\begin{array}{l}{\mathrm{a}} \\ {\mathrm{b}}\end{array}\right) :=\operatorname{Minerr}(\mathrm{a}, \mathrm{b})
    \nonumber \]

    Display optimum values of a and b:

    \[
    \mathrm{a}=4.715 \times 10^{3} \qquad \mathrm{b}=8.906
    \nonumber \]

    Plot of fit:

    \[
    1 :=0.05, 0.1 \ldots 7
    \nonumber \]

    clipboard_ec650f74bfb4aa7c8727faa08cb92c464.png

    Calculate Planck's constant using the value of b, which is equal to (hc)/(kT).

    \[
    \mathrm{h} :=\frac{\mathrm{b} \cdot 10^{-6} \cdot 1.381 \cdot 10^{-23} \cdot 1595}{2.9979 \cdot 10^{8}} \qquad \mathrm{h}=6.544 \times 10^{-34}
    \nonumber \]

    This page titled 1.87: Planck's Radiation Equation Fit to Experimental Data is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Frank Rioux via source content that was edited to the style and standards of the LibreTexts platform.