22.5.4: iv. Problem Solutions

Q1

a. \( T_{nm} \approx \dfrac{|\langle n|V|m \rangle |^2}{\hbar^2\omega_{nm}^2}\)
evaluating \( \langle 1s|V|2s \rangle \) (using only the radial portions of the 1s and 2s wavefunctions since the spherical harmonics will integrate to unity) where V = \((e^2,r):\)

\begin{align} \langle 1s|V|2s \rangle &= \int 2 \left( \dfrac{Z}{a_0} \right)^{\dfrac{3}{2}} e^{\dfrac{-Zr}{a_0}}\dfrac{1}{r}\dfrac{1}{\sqrt{2}}\left( \dfrac{Z}{a_0} \right)^{\dfrac{3}{2}} \left( 1 - \dfrac{Z_r}{2a_0}\right) e^{\dfrac{-Zr}{2a_0}}r^2dr \\ \langle 1s|V|2s \rangle &= \dfrac{2}{\sqrt{2}} \left( \dfrac{Z}{a_0} \right)^{3} \left[ \int re^{\dfrac{-3Zr}{2a_0}}dr - \int \dfrac{Zr^2}{2a_0} e^{\dfrac{-3Zr}{2a_0}}dr \right] \end{align}
Using integral equation 4 for two integration we obtain:
\begin{align} \langle 1s|V|2s \rangle &= \dfrac{2}{\sqrt{2}} \left( \dfrac{Z}{a_0} \right)^3 \left[ \dfrac{1}{\left( \dfrac{3Z}{2a_0} \right)^2} - \left( \dfrac{Z}{2a_0} \right) \dfrac{2}{\left( \dfrac{3Z}{2a_0} \right)} \right] \\ \langle 1s|V|2s \rangle &= \dfrac{2}{\sqrt{2}} \left( \dfrac{Z}{a_0} \right)^3 \left[ \dfrac{2^2a_0^2}{3^2Z^2} - \dfrac{2^3a_0^2}{3^3Z^2} \right] \\ \langle 1s|V|2s \rangle &= \dfrac{2}{\sqrt{2}} \left( \dfrac{Z}{a_0} \right)^3 \left[ \dfrac{(3)2^2a_0^2 - 2^3a_0^2}{3^3Z^2} \right] = \dfrac{8Z}{\sqrt{2}27a_0} \\ Now, & \\ E_n &= -\dfrac{Z^2e^2}{n^22a_0} \text{, } E_{1s} = -\dfrac{Z^2e^2}{2a_0}\text{, } E_{2s} = -\dfrac{Z^2e^2}{8a_0} \text{, } E_{2s} - E_{1s} = \dfrac{3Z^2e^2}{8a_0} \\ So, & \\ T_{mn} &= \dfrac{\left( \dfrac{8Z}{\sqrt{2}27a_0} \right)^2}{\left( \dfrac{3Z^2}{8a_0} \right)} = \dfrac{2^6Z^22^6a_0^2}{(2)3^8a_0^2Z^4} = \dfrac{2^{11}}{3^8Z^2} = 0.312 \text{( for Z = 1)} \end{align}

b. \( \varphi_m (r) = \varphi_{1s} = 2\left( \dfrac{Z}{a_0} \right)^{\dfrac{3}{2}} e^{\dfrac{-Zr}{a_0}} \text{Y}_{00} \)
The orthogonality of the spherical harmonics results in only s-states having non-zero values for \(A_{nm}\). We can then drop the \(Y_{00}\) (integrating this term will only result in unity) in determining the value of \(A_{1s,2s}\).
\begin{align} \psi_n (r) &= \psi_{2s} = \dfrac{1}{\sqrt{2}}\left( \dfrac{Z}{a_0} \right)^{\dfrac{3}{2}} \left( 1 - \dfrac{Zr}{2a_0} \right) e^{\dfrac{-Zr}{2a_0}} \\ \text{Remember for } \varphi_{1s}Z = 1 \text{ and or } \psi_{2s} Z = 2 & \\ A_{nm} =& \int 2 \left( \dfrac{Z}{a_0} \right)^{\dfrac{3}{2}}e^{\dfrac{-Zr}{a_0}}\dfrac{1}{\sqrt{2}} \left( \dfrac{Z + 1}{a_0} \right)^{\dfrac{3}{2}} \left( 1 - \dfrac{( Z + 1)r}{2a_0} \right) e^{\dfrac{-(Z + 1)r}{2a_0}}r^2dr \\ A_{nm} &= \dfrac{2}{\sqrt{2}} \left( \dfrac{Z}{a_0} \right)^{\dfrac{3}{2}} \left( \dfrac{Z + 1}{a_0} \right)^{\dfrac{3}{2}} \int e^{\dfrac{-(3Z + 1)r}{2a_0}} \left(1 - \dfrac{(Z + 1)}{2a_0} \right) r^2dr \\ A_{nm} &= \dfrac{2}{\sqrt{2}}\left( \dfrac{Z}{a_0} \right)^{\dfrac{3}{2}}\left( \dfrac{Z + 1}{a_0} \right)^{\dfrac{3}{2}} \left[ \int r^2 e^{\dfrac{-(3Z + 1)}{2a_0}}dr - \int \dfrac{(Z + 1)r^3}{2a_0}e^{\dfrac{-(3Z + 1)r}{2a_0}} dr \right] \end{align}
Evaluating these integrals using integral equation 4 we obtain:
\begin{align} A_{nm} &= \dfrac{2}{\sqrt{2}}\left( \dfrac{Z}{a_0}\right)^{\dfrac{3}{2}} \left[ \dfrac{2}{\left( \dfrac{3Z + 1}{2a_0} \right)^3} - \left( \dfrac{Z + 1}{2a_0} \right) \dfrac{(3)(2)}{\left( \dfrac{3Z + 1}{2a_0}\right)^4} \right] \\ A_{nm} &= \dfrac{2}{\sqrt{2}}\left( \dfrac{Z}{a_0} \right)^{\dfrac{3}{2}}\left( \dfrac{Z + 1}{a_0} \right)^{\dfrac{3}{2}}\left[ \dfrac{2^4a_0^3}{(3Z + 1)^3} - (Z + 1)\dfrac{(3)2^4a_0^3}{(3Z + 1)^4} \right] \\ A_{nm} &= \dfrac{2}{\sqrt{2}}\left( \dfrac{Z}{a_0} \right)^{\dfrac{3}{2}}\left( \dfrac{Z + 1}{a_0}\right)^{\dfrac{3}{2}}\left[ \dfrac{-2^5a_0^3}{(3Z + 1)^4} \right] \\ A_{nm} &= -2 \dfrac{[2^3Z(Z + 1)]^{\dfrac{3}{2}}}{(3Z + 1)^4} \end{align}
The transition probability is the square of this amplitude:
\[ T_{nm} = \left( -2\dfrac{[2^3Z(Z + 1)]^{\dfrac{3}{2}}}{(3Z + 1)^4} \right)^2 = \dfrac{2^{11}Z^3(Z + 1)^3}{(3Z + 1)^8} = 0.25 \text{ (for Z = 1).} \nonumber \]
The difference in these two results (parts a. and b.) will become negligible at large values of Z when the perturbation becomes less significant as in the case of Z = 1.

Q2

\(\vec{\varepsilon}\) is along Z (lab fixed), and \(\vec{\mu}\) is along z (the C-I module fixed bond). The angle between Z and z is \(\beta\):
\[ \vec{\varepsilon}\dot{\vec{\mu}} = \varepsilon\mu Cos \beta = \varepsilon\mu D^{1*}_{00} (\alpha\beta\gamma ) \nonumber \]
So,
\begin{align} I = \langle D_{M'K'}^{J'} | \vec{\varepsilon}\dot{\vec{\mu}} | D_{MK}^J \rangle &= \int D_{M'K'}^{J'} \vec{\varepsilon}\dot{\vec{\mu}}D_{MK}^J Sin \beta d\beta d\gamma d\alpha \\ &= \varepsilon\mu \int D_{M'K'}^{J'} D_{00}^{1*}D_{MK}^J Sin \beta d\beta d\gamma d\alpha . \\ \text{Now use: } & \\ & D_{M'n'}^{J'*}D_{00}^{1*} = \sum\limits_{jmn} \langle J'M'10 | jm\rangle^*D_{mn}^{j*} \langle jn|J'K' 10\rangle^{*}, \\ \text{to obtain: } & \\ I &= \varepsilon\mu \sum\limits_{jmn} \langle J'M' 10 |jm\rangle *\langle jn |J'K'10 \rangle * \int D_{mm}^{j*}D_{MK}^J Sin \beta d\beta d\gamma d\alpha .\\ \text{ Now use: } & \\ & \int D_{mm}^{j*} D_{MK}^J Sin \beta d\beta d\gamma d\alpha = \dfrac{8\pi^2}{2J + 1} \delta_{Jj}\delta_{Mm}\delta_{Kn}, \\ \text{to obtain: } & \\ I &= \varepsilon\mu \dfrac{8\pi^2}{2J + 1} \sum\limits_{jmn} \langle J'M' 10 |jm \rangle * \langle jn|J'K' 10\rangle *\delta_{Jj}\delta_{Mm}\delta_{Kn} \\ &= \varepsilon\mu \dfrac{8\pi^2}{2J + 1} \langle J'M'10 |JM \rangle \langle JK|J'K'10 \rangle . \\ \text{We use: } & \\ & \langle JK|J'K' 10\rangle = \sqrt{2J + 1}(-i)^{J' - 1 + K)} \begin{pmatrix} J' & 1 & J \\ K' & 0 & K \end{pmatrix} \\ \text{and, } &\\ & \langle J'M'10|JM \rangle = \sqrt{2J + 1}(-i)^{(J' - 1 + M)}\begin{pmatrix} J' & 1 & J \\ M' & 0 & M \end{pmatrix} \\ \text{to give: } & \\ & I = \varepsilon\mu \dfrac{8\pi^2}{2J + 1}\sqrt{2J + 1}(-i)^{(J' - 1 + M)}\begin{pmatrix} J' & 1 & J \\ M' & 0 & M \end{pmatrix}\sqrt{2J + 1}(-i)^{(J' - 1 + K)}\begin{pmatrix} J' & 1 & J \\ K' & 0 & K \end{pmatrix} \\ & = \varepsilon\mu 8\pi^2 (-i)^{(J' - 1 + M + J' - 1 + K)}\begin{pmatrix} J' & 1 & J \\ M' & 0 & M \end{pmatrix} \begin{pmatrix} J' & 1 & J \\ K' & 0 & K \end{pmatrix} \\ & = \varepsilon\mu 8\pi^2 (-i)^{(M + K)}\begin{pmatrix} J' & 1 & J \\ M' & 0 & M \end{pmatrix} \begin{pmatrix} J' & 1 & J \\ K' & 0 & K \end{pmatrix} \end{align}
The 3-J symbols vanish unless: K' + 0 = K and M' + 0 = M.
So,
\[ I = \varepsilon\mu 8 \pi^2 (-i)^{(M + K)}\begin{pmatrix} J' & 1 & J \\ M & 0 & M \end{pmatrix}\begin{pmatrix} J' & 1 & J \\ K & 0 & K \end{pmatrix} \delta_{M'M}\delta_{K'K} \nonumber \]
b. \( \begin{pmatrix} J' & 1 & J \\ M & 0 & M \end{pmatrix} \) and \( \begin{pmatrix} J' & 1 & J \\ K & 0 & K \end{pmatrix} \) vanish unless J' = J + 1, J, J - 1\(\therefore \Delta J = \pm 1, 0\)
The K quantum number can not change because the dipole moment lies along the molecule's \(C_3\) axis and the light's electric field thus can exert no torque that twists the molecule about this axis. As a result, the light can not induce transitions that excite the molecule's spinning motion about this axis.

Q3

a. B atom: \(as^22s^22p^1 \text{, }^2P\) ground state L = 1, S = \(\dfrac{1}{2}\), gives degeneracy ((2L + 1)(2S + 1)) of 6.
O atom: \(1s^22s^22p^4\), \(^2P\) ground state L = 1, S = 1, gives a degeneracy ((2L + 1)(2S + 1)) of 9.
The total number of states formed is then (6)(0) = 54.
b. We need only consider the p orbitals to find the low lying molecular states:

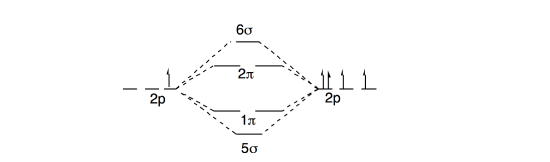
Which, in reality look like this:

This is the correct ordering to give a \(^2\sum^+\) ground state. The only low-lying electron configurations are \(1\pi^35\sigma^2 \text{ or } 1\pi^45\sigma^1\). These lead to \(^2\Pi \text{ and } ^2\Sum^+\) states, respectively.
c. The bond orders in both states are \(2\dfrac{1}{2}\).
d. The \( ^2\sum\) is + and g/u cannot be specified since this is a heteronuclear molecule.
e. Only one excited state, the \(^2\Pi\), is spin-allowed to radiate to the \(^2\sum^+\). Consider symmetries of transitio moment operators that arise in the E1, E2 and M1 contributions to the transition rate
Electric dipole allowed: \( z \rightarrow \sum^+, x, y \rightarrow \Pi , \therefore \text{ the } ^2\Pi \rightarrow ^2\sum^+\) is electric dipole allowed via a perpendicular band.
Magnetic dipole allowed: \( R_z \rightarrow \sum^-, R_{x,y} \rightarrow \Pi , \therefore \text{ the } ^\sum /rightarrow ^2\sum^+\) is magnetic dipole allowed.
Electric quadrupole allowed: \( x^2 + y^2, z^2 \rightarrow \sum^+, xy, yz \rightarrow \Pi, x^2 - y^2, xy \rightarrow \Delta \therefore \text{ the } ^2\Pi \rightarrow ^2\sum^+\) is electric quadrupole allowed as well.
f. Since ionization will remove a bonding electron, the BO\(^+\) bond is weaker than the BO bond.
g. The ground state BO\(^+\) is \(^1\sum^+\) corresponding to a \(^1\pi^4\) electron configuration. An electron configuration of \(1\pi^3 5\sigma^1\) leads to a \(^3\Pi\) and a \(^1\Pi\) state. The \(^3Pi\) will be lower in energy. A \(1\pi^2 5\sigma^2\) confirmation will lead to higher lying states of \(^3\sum^- , ^1\Delta, \text{ and } ^1\sum^+\).
h. There should be 3 bands corresponding to formation of BO\(^+\) in the \(^1\sum^+, ^3\Pi \text{, and } ^\Pi\) states. Since each of these involves removing a bonding electron, the Franck-Conden integrals will be appreciable for several vibrational levels, and thus a vibrational progression should be observed.

Q4

a. The bending \((\pi )\) vibration is degenerate.
b. \begin{align} H--&-C\equiv N \\ \Uparrow & \\ & \text{bending fundamental} \end{align}
c. \begin{align} H--&-C\equiv N \\ \Uparrow & \\ & \text{stretching fundamental} \end{align}
d. CH stretch (\(\nu_3\) in figure) is \(\sigma\) CN stretch is \(\sigma\) and HCN \((\nu_2\) in figure) bend is \(\pi\).
e. Under z \((\sigma )\)light the CN stretch and the CH stretch can be exited, since \(\psi_0 = \sigma, \psi_1 = \sigma \text{ and } z = \sigma\) provides coupling.
f. Under x,y (\(\pi\)) light the HCN bend can be excited, since \(\psi_0 = \sigma, \psi_1 = \pi\) and x,y = \(\pi\) provides coupling.
g. The bending vibration is active under (x,y) perpendicular polarized light. \( \Delta J = 0, \pm 1\) are the selection rules for \(\perp\) transitions. The CH stretching vibration is active under (z) \(\|\) polarized light. \(\Delta J = \pm 1\) are the selection rules for \(\|\) transitions.